Article Search
Volume 27.1
January–April 2024
Full table of contents
ISSN: 1094-8074, web version;
1935-3952, print version
Recent Research Articles
See all articles in 27.1 January-April 2024
See all articles in 26.3 September-December 2023
See all articles in 26.2 May-August 2023
See all articles in 26.1 January-April 2023
 Lluís Gil
Lluís Gil
Universitat Politècnica de Catalunya – BarcelonaTech
08222, Terrassa
Spain
Lluis.gil@upc.edu
Lluís Gil (Barcelona, 1966) achieved a civil engineering degree in 1992 and a PhD from Universitat Politecnica de Catalunya UPC in 1997. He currently is associate professor at UPC in the field of aerospace structures. Director of research Laboratory for the Innovation of Structures and Materials (LITEM). Lecturer of continuum mechanics and engineering structures. Interested in NDT, composites and new materials. ORCID:0000-0002-2007-4846.

 Jordi Marcé-Nogué
Jordi Marcé-Nogué
Universitat Politècnica de Catalunya – BarcelonaTech
ETSEIAT, c/colom 11, edifici TR45
08222, Terrassa
Spain
and
Institut Català de Paleontologia
Edifici ICP, Universitat Autònoma de Barcelona, Campus de Bellaterra
08193, Cerdanyola del Vallès
Spain
Jordi.marce@upc.edu / +34 937398018
Jordi Marcé-Nogué (Igualada, 1979) has Bachelor degree of Industrial Engineering issued from Universitat Politècnica de Catalunya (Spain) in 2003 and PhD degree Resistència de Materials i Computational Biomechanics from Universitat Politècnica de Catalunya in 2009.
He started as a research fellow in the Departament de Estructures a l'Enginyeria and from 2006 he has being a assistant teacher in Escola Tècnica Superior d'Enginyeria i Aeronàutica de Terrassa (UPC) and a researcher at Laboratory for the Innovation of Structures and Materials (LITEM)

 Montserrat Sánchez
Montserrat Sánchez
Universitat Politècnica de Catalunya – BarcelonaTech
08222, Terrassa
Spain
Montserrat.sanchez@upc.edu
Dr. Mechanical Engineer and professor at the Universitat Politècnica de Catalunya. She has participated in several national projects and agreements with companies. She is currently directing two doctoral theses, has participated in 12 competitive research projects (2 of them as principal investigator), has conducted 15 international publications and 12 conference contributions.

FIGURE S1. Von Mises stress and strain distributions and the displacement field distribution for Connochaetes taurinus and Alcelaphus buselaphus when elastic modulus is E=10000 MPa, E=25000 MPa and E=50000 MPa for a homogeneous material (case A) when the coloured scale in the legend is the same for the three cases.
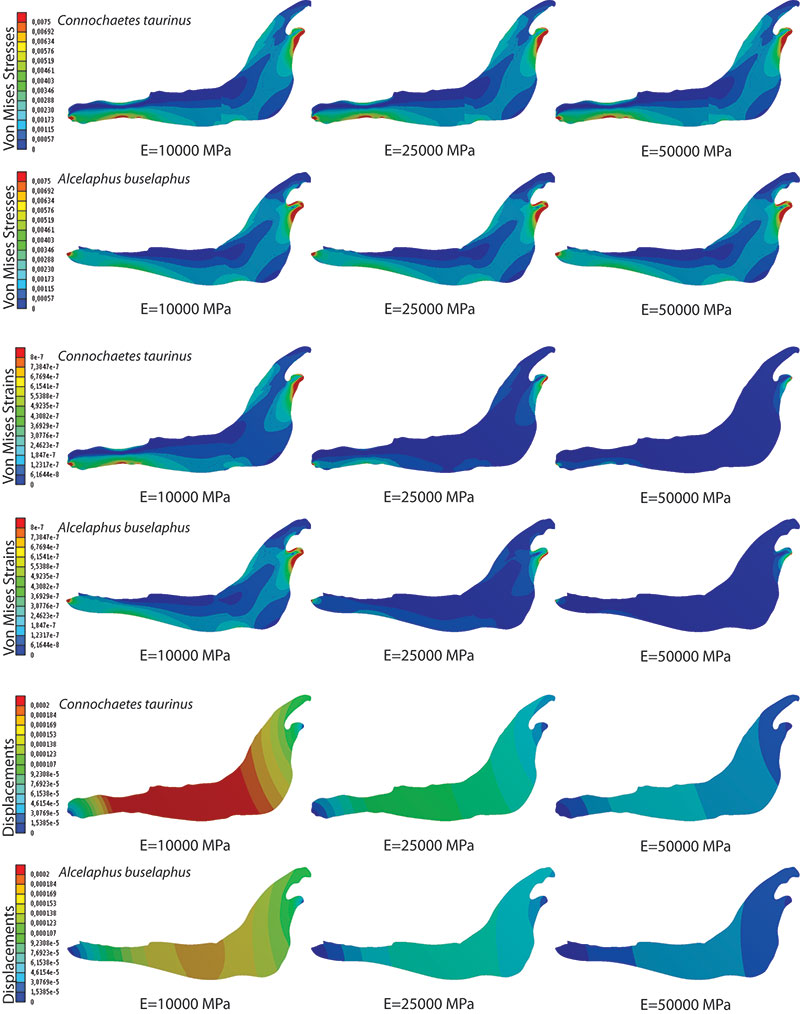
FIGURE S2. Von Mises stress and strain distributions and the displacement field distribution for Connochaetes taurinus and Alcelaphus buselaphus when elastic modulus is E=10000 MPa, E=25000 MPa and E=50000 MPa for a non-homogeneous material (case B) when the coloured scale in the legend is the same for the three cases.
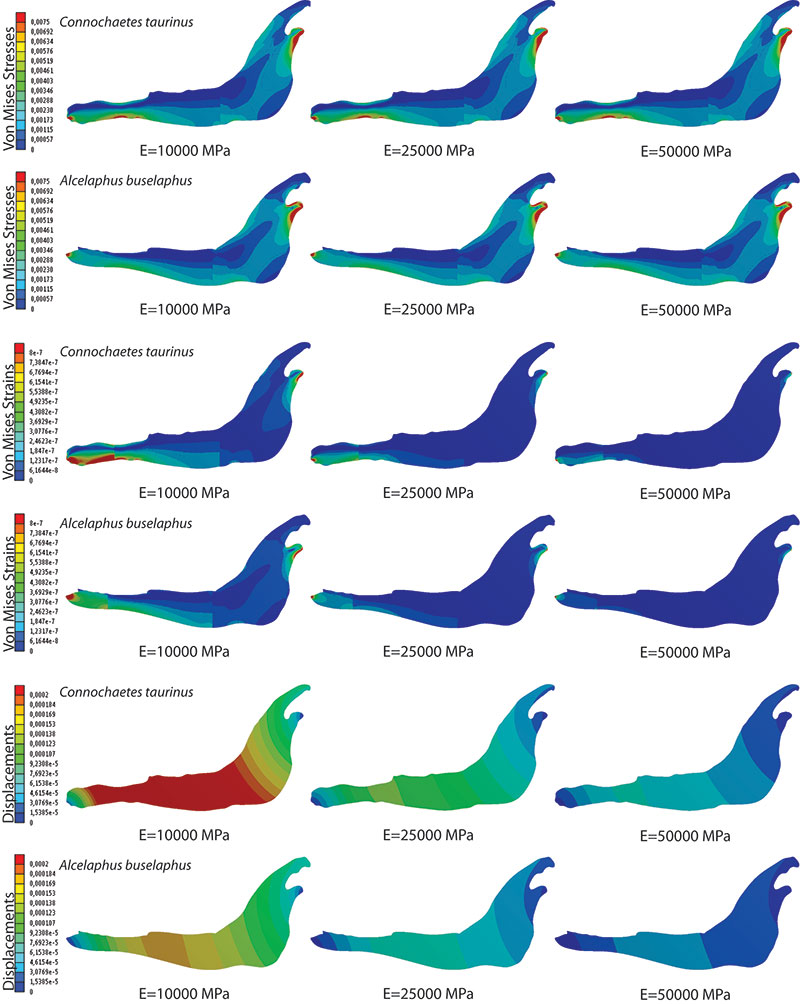
TABLE S1. Numericla results in points P and Q for a homogeneous material: Von Mises Stresses, Von Mises Strains and displacements in front of the variation of the Elastic Modulus (E).
TABLE S2. Numerical results of Von Mises Stresses, Von Mises Strains and displacements for a homogeneous material in points P and Q for the relationship between the value depending of the variation of the Elastic Modulus (E) and the reference value (E=10000 MPa).
TABLE S3. Numerical results in points P and Q for a homogeneous material: Maximum and mínimum Principals Stresses and Strains and Strain energy in front of the variation of the Elastic Modulus (E).
TABLE S4. Numerical results in points P and Q for a homogeneous material: Maximum and mínimum Principals Stresses and Strains and Strain energy for the relationship between the value depending of the variation of the Elastic Modulus (E) and the reference value (E=10000 MPa).
TABLE S5. Numericla results in points P and Q for a non-homogeneous material: Von Mises Stresses, Von Mises Strains and displacements in front of the variation of the Elastic Modulus (E).
TABLE S6. Numerical results of Von Mises Stresses, Von Mises Strains and displacements for a non-homogeneous material in points P and Q for the relationship between the value depending of the variation of the Elastic Modulus (E) and the reference value (E=10000 MPa).
TABLE S7. Numerical results in points P and Q for a non-homogeneous material: Maximum and mínimum Principals Stresses and Strains and Strain energy in front of the variation of the Elastic Modulus (E).
TABLE S8. Numerical results in points P and Q for a non-homogeneous material: Maximum and mínimum Principals Stresses and Strains and Strain energy for the relationship between the value depending of the variation of the Elastic Modulus (E) and the reference value (E=10000 MPa).
FIGURE 1. Boundary conditions, forces applied in the studied jaws, location of points P and Q and separated regions where the Non-homogeneous properties are applied for the Connochaetes taurinus and Alcelaphus buselaphus.
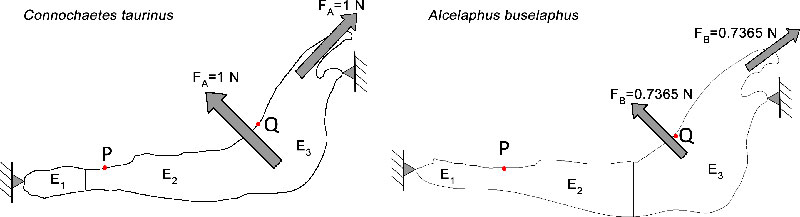
FIGURE 2. von Mises Stress Distribution, von mises strain distribution and Displacement field distribution for Connochaetes taurinus and Alcelaphus buselaphus when elastic modulus is E=10000 MPa, E=25000 MPa and E=50000 MPa for a homogeneous material (case A).
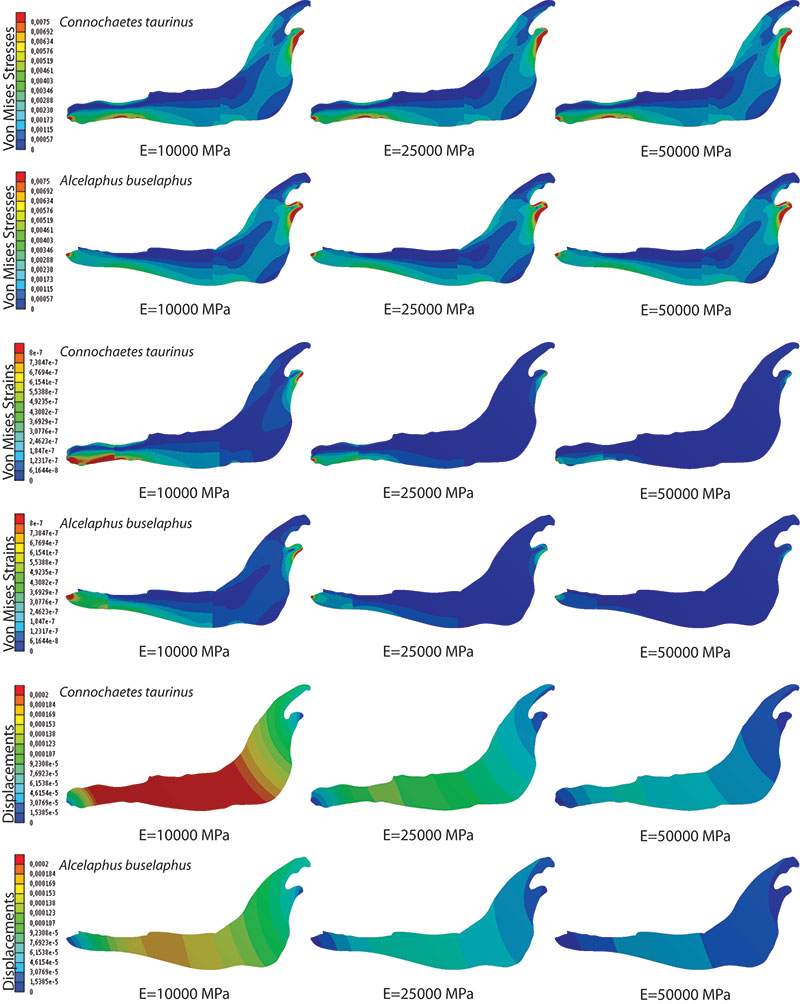
FIGURE 3. 3.1 von Mises stresses, 3.2 von Mises strains, 3.3 Displacements, 3.4 von Mises stress relationship with reference value, 3.5 von Mises strain relationship with reference value and 3.6 Displacement relationship with reference value in front of variation in the elastic modulus (E) in points P and Q.
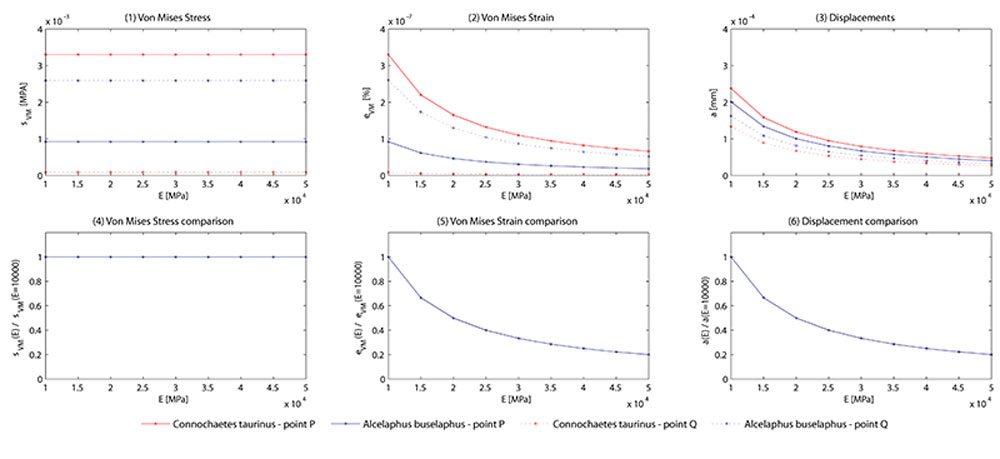
FIGURE 4. von Mises Stress Distribution, von Mises strain distribution and displacement field distribution for Connochaetes taurinus and Alcelaphus buselaphus when elastic modulus is E=10000 MPa, E=25000 MPa and E=50000 MPa for a non-homogeneous material (case B).
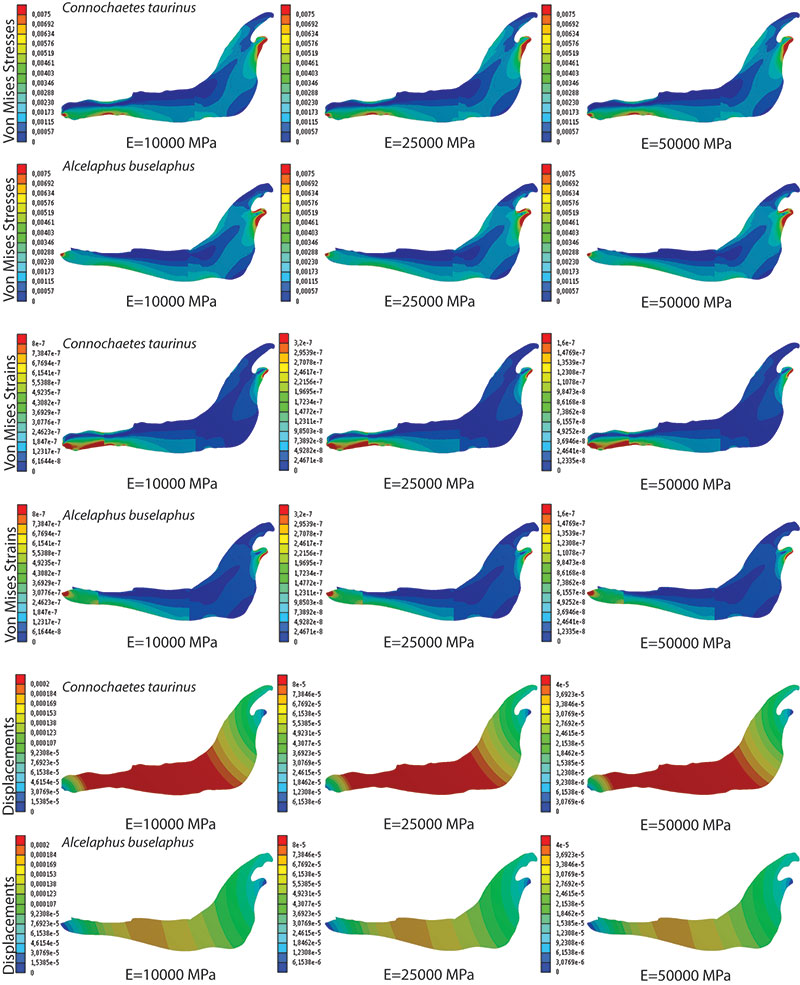
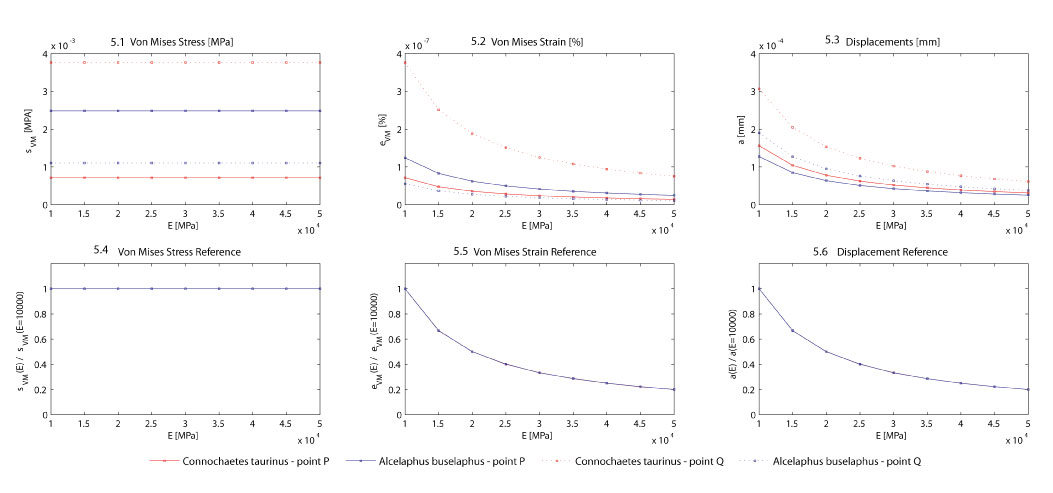
FIGURE 5. 5.1 von Mises stresses, 5.2 von Mises strains, 5.3 Displacements, 5.4 von Mises stress relationship with reference value, 5.5 von Mises strain relationship with reference value and 5.6 Displacement relationship with reference value in front of variation in the elastic modulus (E) in points P and Q.
Insights into the controversy over materials data for the comparison of biomechanical performance in vertebrates
Plain Language Abstract
Palaeobiology uses computation as a valuable tool for simulating the mechanical performance of extinct species and establish comparisons among them. Models need material properties of bones, etc. Nevertheless, this data is unknown for extinct species. This work studies the influence of material properties over results and comparative metrics like stresses, strains or displacements. Using continuum mechanics theory it is possible to show a paradox: no matter what material properties you use the comparative patterns between species will be correct. In all other cases, the sensitivity of material properties is limited.
Resumen en Español
Nueva aproximación en torno a la controversia sobre los datos de materiales para la comparación del rendimiento biomecánico en los vertebrados
La comparación del comportamiento mecánico de diferentes especies se realiza con ayuda de herramientas computacionales como el Análisis de Elementos Finitos FEA. En paleobiología es común considerar el hueso como un material isotrópico para simulaciones, pero a menudo es imposible conocer los datos reales de los materiales óseos. Este trabajo investiga la influencia de la elección de las propiedades de los materiales óseos en los resultados de simulaciones computacionales mostrando cuándo y por qué los datos de materiales van a ser relevantes y cuándo la selección de estos datos puede ser irrelevante. A partir del enfoque teórico de la mecánica de medios continuos y con un ejemplo práctico se analiza la relación entre los datos del material en medidas comparativas como tensiones, deformaciones y desplazamientos. Cuando en un análisis comparativo en el material se asumen propiedades lineales y elásticas, el efecto del módulo elástico del material no afecta los patrones de tensión. Esta afirmación es cierta para materiales homogéneos y no homogéneos; en este último caso la proporción entre las propiedades de los diferentes materiales debe mantenerse constante. En el caso de deformaciones y desplazamientos, hay una constante de proporcionalidad inversa, entre los valores medidos y los cambios aplicados en el módulo elástico. Esta característica en los valores del módulo elástico permite realizar estudios comparativos sin considerar las propiedades reales de los materiales elásticos.
Palabras clave: análisis de elementos finitos; propiedades de los materiales; huesos; mecánica de medios continuos; análisis comparativo
Traducción: Enrique Peñalver
Résumé en Français
Regards sur la controverse des données des matériaux pour la comparaison de la performance biomécanique chez les vertébrés
La comparaison mécanique des différentes espèces est effectuée à l'aide d'outils informatiques comme Finite Element Analysis FEA. Dans la paléobiologie, il est courant de considérer l'os comme un matériau isotrope pour les simulations mais il est souvent impossible de savoir les données réelles de matériaux osseux. Ce travail étudie l'influence du choix des propriétés des matériaux osseux sur les résultats des simulations, montrant quand et pourquoi les données sur les matériaux sont pertinentes et lorsque la sélection de ces données devient inutile. Une approche théorique de la mécanique des milieux continus et avec un exemple concret de la relation entre les données matérielles et des mesures comparatives comme le stress, les tensions et les déplacements est discutée. Lorsque des propriétés de matériaux linéaires et élastiques sont supposées dans une analyse comparative, l'effet du module d'élasticité du matériau n'est pas pertinent au cours des modes de stress. Cette affirmation est vraie pour les matériaux homogènes et non homogènes, dans ce dernier cas la proportion entre les différentes propriétés des matériaux doit être maintenue constante. Dans le cas des tensions et des déplacements, il existe une proportionnalité inverse maintenu constamment, entre les valeurs de la métrique et de l'évolution du module élastique. Ces propriétés permettent des études comparatives sans tenir compte des propriétés réelles des matériaux élastiques.
Mots-clés: analyse par éléments finis; propriétés des matériaux; os; mécanique des milieux continus; analyse comparative
Translator: Kenny J. Travouillon
Deutsche Zusammenfassung
Erkenntnisse über die Kontroverse von Materialdaten beim Vergleichen biomechanischer Leistungen von Vertebraten
Es werden Vergleiche von verschiedenen Arten auf mechanischer Ebene mit Hilfe computergestützter Instrumente wie Finite Element Analyse (FEA) durchgeführt. In der Paläobiologie ist es bei Simulationen üblich Knochen als isotropes Material anzusehen, jedoch wissen wir die tatsächlichen Daten des Knochenmaterials oft nicht genau. Diese Arbeit untersucht den Einfluss bei der Wahl von Knochenmaterialeigenschaften über die Ergebnisse von Simulationen und zeigt wann und warum die Materialdaten relevant sind und wann die Auswahl dieser Daten irrelevant wird. Mit der theoretischen Herangehensweise aus der Kontinuumsmechanik und mit praktischen Beispielen wird der Zusammenhang zwischen Materialdaten und vergleichenden Maßen wie Druck, Zug und Verformung diskutiert. Wenn bei einer vergleichenden Analyse lineare und elastische Materialeigenschaften angenommen werden, ist der Effekt des elastischen Materialmoduls irrelevant gegenüber den Spannungsmustern. Diese Aussage trifft auf homogene und inhomogene Materialien zu, bei letzterem Fall müssen die Proportionen zwischen den verschiedenen Materialeigenschaften konstant gehalten werden. Im Falle von Zug und Verformung wird eine inverse Proportionalität konstant gehalten, zwischen den Maßen der Werte und den Veränderungen in den elastischen Modulen. Diese Eigenschaften erlauben vergleichende Untersuchungen ohne die echten elastischen Materialeigenschaften zu berücksichtigen.
Schlüsselwörter: Finite Element Analyse; Materialeigenschaften; Knochen; Kontinuumsmechanik; vergleichende Analyse
Translator: Eva Gebauer
Arabic

Translator: Ashraf M.T. Elewa
-
-
-
Review: The Princeton Field Guide to Mesozoic Sea Reptiles
 The Princeton Field Guide to Mesozoic Sea Reptiles
The Princeton Field Guide to Mesozoic Sea ReptilesArticle number: 26.1.1R
April 2023


 Poster Winners 2024
Poster Winners 2024