INTRODUCTION

Among the externally shelled cephalopods, wall-like septa separate the shell into camerae and form sutures where each septum joins the external shell. The shape of the suture has been used to distinguish cephalopod species and determine taxonomic relationships, and often serves as a proxy for examining the function of the septa, which has been the focus of much attention in recent years. Although diagnostic and important, the numerical description of sutures has been elusive. This paper presents a numerical method for describing suture patterns and briefly investigates its application.

The terms "suture," "suture line" and "suture pattern" have been used synonymously by various authors. In this paper, "suture" refers to the juncture of the septum and the shell wall, and is a structural part of the cephalopod shell. This paper does not consider the suture. "Suture line" refers to the graphical representation of that juncture on the shell, and is typically drawn in two dimensions. This paper presents a method to reconstruct the suture line using a mathematical description based on Fourier series. A simulation would create suture lines from the physical processes which govern them; this paper does not present a method of simulation. "Suture pattern" refers to the shape or form of the suture line. This paper presents some suggestions for analyzing and comparing suture patterns.

Suture patterns range from simple, straight lines (nautilitic patterns) to visually complex and intricate curves (ammonitic patterns). No explanation of sutural complexity is universally accepted. Proposed explanations focus upon a link between sutural complexity and the shell's resistance to breaking due to hydrostatic or unidirectional stresses (Hewitt and Westermann 1986, 1997, Westermann and Tsujita 1999), the participation of the septa in processes regulating buoyancy (Reyment 1958, Saunders 1995, Seilacher and LaBarbera 1995), or other factors (e.g., viscous fingering, García-Ruíz et al. 1990; body-conch attachment, Lewy 2002). Quantitative modeling experiments of the effect of sutural complexity on shell strength have used artificially simple sinusoidal suture patterns with one or more frequencies (Daniel et al. 1997, Hassan et al. 2002). The inability to mathematically describe more complex and realistic suture patterns limits such analyses. (For more detailed and complete reviews of this debate, see Jacobs 1996, Seilacher and LaBarbera 1995, Westermann 1996, Daniel et al. 1997, Olóriz et al. 2002, Lewy 2002.)

To date, quantitative measures of suture patterns fall into two general categories: statistics and descriptions. Statistics are single values that describe some aspect of the pattern that is usually construed as a measure of sutural complexity: a number that increases with the suture's visual complexity. Exactly what is meant by "complexity" is vague (McShea 1991); one reason such a statistic is pursued is to clarify its meaning. Descriptions, on the other hand, attempt to provide a mathematical method by which the patterns can be recreated numerically and do not address complexity. These methods describe the shape of the suture pattern, and therefore must contain more values than a single statistic. Unlike a statistic, a mathematical description of any suture pattern is unique to that pattern.

Westermann proposed the length of a suture normalized to the circumference of the phragmacone as a measure of sutural complexity (sutural complexity index, Westermann 1971) Other workers adopted this statistic (e.g., the Index of Sutural Complexity, Ward 1980; suture-sinuosity index, Saunders 1995) or a variation of it (Suture Complexity Index, Saunders 1995). These statistics have been used to study a variety of paleobiological problems (Ward 1980, Saunders 1995, Saunders and Work 1996, 1997). This statistic has the same value for suture patterns of very different shapes.

Fractal dimension is an alternative statistic to the sutural complexity index. Fractal dimension (F.D., Boyajian and Lutz 1992; Df, Olóriz et al. 1999) more directly measures recurving of a suture pattern. The first application of fractal dimension to suture patterns used a space-filling method (Boyajian and Lutz 1992, Lutz and Boyajian 1995), and more recent applications use the more conventional step-line method (Olóriz et al. 1999). The values of fractal dimension are different between the two methods. Fractal analysis has been applied to a variety of paleobiological problems (Olóriz and Palmqvist 1995, Olóriz et al. 1997), including the function of the septum (Olóriz et al. 2002). Like the sutural complexity index, different suture patterns share the same value for fractal dimension.

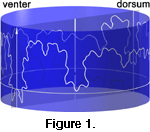Several attempts have been made to devise a numerical description of suture patterns. The general form of suture lines, a closed orbit wrapping around the circumference of the phragmacone (Figure 1), has been recognized as periodic and therefore potentially amenable to Fourier analysis. There is motivation for applying Fourier methods to sutures, as they have proven useful for morphometric analyses of ostracodes (Kaesler and Waters 1972), bivalves (Gevirtz 1976), bryozoans (Anstey and Delmet 1972, 1973, Anstey et al. 1976, Anstey and Pachut 1980), trilobites (Foote 1990), humans (Palmqvist et al. 1996) and other taxa.

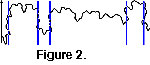The complexity of suture patterns, particularly of ammonitic patterns, precludes the direct application of Fourier methods due to non-unique points (Figure 2). It is not uncommon for a suture pattern to recurve along its length, so that there is more than one height for a single angular position around the circumference of the phragmacone. Less-detailed nautilitic suture patterns can be studied using Fourier analysis because they lack non-unique points, but more elaborate ammonitic patterns cannot (Canfield and Anstey 1981). A previous study attempted to circumvent the problem via a transformation (Gildner and Ackerly 1985), but fails due to a dependence upon the scale of measurement.

The method described in this paper consists of three parts: a parametric formulation for points along the suture line, a transformation of the data, and a normalization of the series by trigonometric interpolation. The parametric formulation removes the problem of non-unique points. The transformation solves the recognized problem confronted when using Fourier methods on angular data: the removal of the trend of increasing angle around the circumference of the feature. This is analogous to the perimeter method (Foote 1989), originally applied to describe trilobite cranidia as non-parametric, planar curves in polar coordinates. This study extends Foote's method into three dimensions. The trigonometric interpolation is not necessary for the description of a suture pattern but is needed to standardize such descriptions for comparisons between suture patterns. The index of the point along the suture line is used as the independent variable to calculate an initial pair of Fourier series from digitized suture patterns, which are then used to interpolate points for the calculation of final, normalized Fourier series. The final series allows the numerical analysis of single suture patterns, and the comparison of different suture patterns. This paper will briefly examine how ontogenetic development and similarity between suture patterns may be approached using this method.

Suture patterns from the literature were transformed into digital images using a flat-bed scanner. The images were manually digitized directly on the computer, and the series were calculated from the digitized data using a discrete Fourier transform. The suture patterns were reconstructed using the series, and points equally spaced along the suture line were trigonometrically interpolated using the series. The final, normalized Fourier series were calculated from the interpolated data. Digitization of the images was done with a program written by the author in Java (Frames); other processing was done with programs written by the author in REALbasic, compiled for Mac OS X . The code and programs are available for the three programs: Draw4096, Frames, and BothFourier.