The equivalence between Lande's (1979) formulation of multivariate evolution and the shape-space simulation adopted here can be demonstrated as follows. Let Z be a matrix of n phenotypic traits measured on m individuals, which are distributed normally with some amount of covariance. The vector of trait means is . Let P be the n by n phenotypic covariance matrix of z, and let be a vector of selection differentials of length n postmultiplied by matrix H representing the heritability of P. Each selection differential is the standardized difference between trait means in selected and unselected adults (Lande 1979; Falconer and Mackay 1996).

Lande's equation for change in the multivariate mean in response to selection over one generation can then be written as follows:

(A1)

where is the change in means of traits Z after one generation of selection (Lande 1979). Lande's original formula used G, the additive-genetic covariance matrix, instead of P, but G is equal to the heritable portion of the phenotypic covariance matrix, or HP.

The morphological shape-space in which the simulation is performed is described by matrices obtained by the singular-value decomposition (SVD) of P,

  (A2)

where U is the left singular vector matrix representing the weights of the original variables on the principal component vectors (equivalent to the eigenvectors, Table 2), W is the diagonal matrix of the singular values representing the variances of the data on the principal components vectors (equivalent to the eigenvalues, Table 2), V is the right singular vector matrix, and the superscript ^T represents the transpose of the matrix (Golub and Van Loan 1983). U functions as a j by n rotation matrix used to transform data from the original coordinate system to the principal components axes (or back again), where j is the matrix rank of P. When P is not singular then j = i, but when P is singular, as with Procrustes superimposed shape data, j is smaller than i. W is a j length diagonal matrix that can be thought of as P transformed so that trait covariances are zero. Note that for real, positive definite symmetric matrices U and V are equal. The projections of the original data onto the principal components (the scores) are given by

(A3)

where Z´ are the scores (Jolicoeur and Mosimann 1960). The total variances in Z and Z´ are equal, but covariances are absent in Z´ and the variances of Z´ are given by W.

Now, let at time 0 be = {0, 0, ... i}. The projection of  onto the principal components axes is which equals {0, 0, ... j}. The vector of mean morphologies in the next generation, , equals or HP. The projection of into the principal components space is

(A4)

which, by substitution, equals

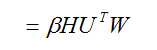
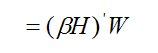(A5)

Importantly, solving for in Eq. A4 reveals that the transformation back into the original coordinate space only requires multiplication by U, such that

(A6)

Equations A5 and A6 show that simulations can be carried out in principal components space using only a vector of selection differentials and W, which can be treated as a vector of scaling weights. A simulation in reduced-dimension shape-space is thus computationally more efficient than one in the original space because (H) is of length j and requires fewer operations than H of length n and because multiplication by vector W takes fewer calculations than multiplication by covariance matrix P. At the end of the simulation, the results can easily be transformed back to the original coordinate space by multiplying them by U.

Simulation in principal components space also overcomes complications introduced by the singularity of P when it is based on Procrustes superimposed data. Procrustes fitting removes rotation, translation, and scaling from the data, resulting in a covariance matrix of reduced rank (Rohlf 1999; Dryden and Mardia 1998). The singularity can produce seemingly odd results when a uniform vector of selection differentials is applied to Eq. A1. For example if H = {1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1} were applied to P from the Bialowieza sample, the resulting = {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}. This result is counterintuitive because we seem to have applied uniform positive selection to the system but have obtained no change in phenotype. The colinearity of the matrix has the effect of cancelling the effects of the uniform selection vector. When uniform positive selection is applied in principal components space as (H) = {1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1} we get a pleasing that moves the mean phenotypic in a positive direction along each principal component. The same change could be produced in the original coordinate space, but only by using the counterintuitive vector of selection differentials H = {-0.121, -0.012, 0.268, 0.883, -0.929, -1.114, -0.199, -0.432, 2.464, 0.797, 0.219, 0.824, -0.699, -0.835, -1.58, 0.343, 0.583, -0.454}. This situation makes an intuitive simulation of positive directional selection exceedingly difficult unless it is performed in the reduced dimension shape-space.