"A second reason for giving theoretical morphology a good run for its money is that, in many ways, it is unlike other sciences. In A New Kind of Science (2002) Stephen Wolfram has controversially suggested that science in the future will be more concerned with algorithms than laws. One wonders how that could be true of all science, but if there is any science of which this is clearly true, that science is theoretical morphology."

The inspiration for "theoretical morphology" (Raup and Michelson 1965) lies in the morphogenetic simulation of actual growth processes in nature and in the search for the general growth "rules" governing the generation of biological form. In this aspect of the discipline, it can be viewed as an algorithmic approach to the analysis of evolutionary development, as opposed to an experimental one. Yet theoretical morphology is much more than "Computer EvoDevo"! The developmental models created in a theoretical morphologic analysis can be used not only to simulate existing biological form, but also to generate hypothetical biological form that, although geometrically possible, has never been evolved by any known living organisms on Earth. The very existence of nonexistent form is of immediate significance to the evolutionary theorist—why hasn't nature produced this form? The answer to this question leads both the theorist and experimentalist to the analysis of the roles of adaptation, natural selection, and evolutionary constraint in the shaping of biological form (for a more extensive discussion of the analytic techniques of theoretical morphology see McGhee 1999, 2001, 2007).

Many years ago, we became interested in the intricate and elegant helical colony forms evolved by species of the bryozoan genus Archimedes (McKinney and Raup 1982). Although Archimedes is long extinct, similar helical colony forms have been convergently evolved in species of the living genus Bugula turrita (McKinney 1980). In fact, further analysis has revealed that helical colony forms have been convergently, independently, evolved no less that six separate times within the Phylum Bryozoa (McKinney and McGhee 2003). Why have bryozoan colonies repeatedly evolved helically coiled colonies? And how do they produce these colony forms? Lastly, are there geometrically possible helical forms that they have never produced, and why not? These questions are of the very essence of theoretical morphology.

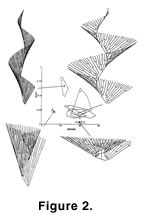
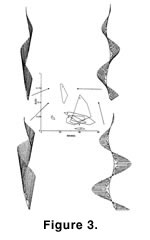
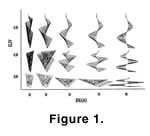In our initial studies, we demonstrated that the helical colony form—although very intricate in appearance—could be computer simulated by a model having only five geometric parameters (McKinney and Raup 1982). Thus, far from being difficult to develop, the fact that the morphogenesis of helical colonies is algorithmically simple may be a large factor in its repeated evolution within the bryozoans. In our subsequent studies, we have taken the geometric parameters of the helical colony model and created a theoretical morphospace of hypothetical, and potential, bryozoan colony form (Figure 1). Exploration of this morphospace to date has revealed that it is very unevenly filled by actual bryozoans through geologic time, and that the "full" (Figure 2) versus "empty" (Figure 3) regions of the morphospace appear largely to be due to functional constraints – that is, the existent forms make efficient filtering geometries, and the nonexistent forms do not (McGhee and McKinney 2000, 2002; McKinney and McGhee 2003, 2004).

In the spirit of Stephen Wolfram's (2002) vision of a science "more concerned with algorithms than laws," we are making available the algorithms of the helical colonies model in this brief paper. We feel we have just scratched the surface of understanding why these intricate forms have convergently reappeared during bryozoan evolution, and we wish to make the code available for others to experiment with. We also encourage others to take the code and modify it to simulate other helical aspects of form in nature, beyond those found (or not found) within the Bryozoa.