Volume 28.2
May–August 2025
Full table of contents
ISSN: 1094-8074, web version;
1935-3952, print version
Recent Research Articles
See all articles in 28.2 May-August 2025
See all articles in 28.1 January-April 2025
See all articles in 27.3 September-December 2024
See all articles in 27.2 May-August 2024
Interested in submitting a paper to Palaeontologia Electronica?
Click here to register and submit.
Article Search

Authors (left to right): Eric Snively, John R. Cotton, Ryan Ridgely, and Lawrence M. Witmer.
Eric Snively
Department of Mechanical Engineering
Russ College of Engineering
249 Stocker Center
Ohio University,
Athens, OH 45701
USA
Eric Snively is a post-doctoral researcher and instructor at Ohio University. His graduate work at the University of Calgary and Ohio University emphasized feeding and locomotor function in carnivorous dinosaurs. He contributed to field education with the Royal Tyrrell Museum, and raptor outreach with the Calgary Wildlife Rehabilitation Society. He taught and mentored students at Villanova University, Ohio University, and as an Ingenuity fellow at the University of Alberta. His research seeks to infer function and behavior of fossil animals (including dinosaurs and ceteartiodactyls), using finite element analysis, dynamics, and new statistical methods.
![]()
John R. Cotton
Department of Mechanical Engineering
Russ College of Engineering
249 Stocker Center
Ohio University
Athens, OH 45701
USA
John Cotton is Assistant Professor of Mechanical Engineering and Biomedical Engineering at Ohio University. He received his Ph.D. from Virginia Tech in 1998 in Engineering Mechanics, where his research focused on simulating the deformation of hair cell bundles to better understand mechanotransduction in the inner-ear. As a postdoc at the University of Southampton he developed methods to simulate fatigue damage in bone. His research is broadly concerned with characterizing the mechanical properties of biological structures, as well as simulating their mechanical response using finite element and other numerical modeling techniques.
![]()
Ryan Ridgely
Department of Biomedical Sciences
Heritage College of Osteopathic Medicine
Ohio University
Athens, OH 45701
USA
Ryan Ridgely graduated from the University of Rhode Island in 2000. He is an integral member of the Witmer lab where he is a research technician participating in NSF grant collaborations on cephalic anatomy evolution in dinosaurs. His major area of work is in digital morphology, which is working with CT (CAT) scans and MR imaging to produce 3D visualization models of internal anatomy in modern and extinct vertebrates.
![]()
Lawrence M. Witmer
Department of Biomedical Sciences
Heritage College of Osteopathic Medicine
Ohio University
Athens, OH 45701
USA
Lawrence M. Witmer is a Professor of Anatomy at the Ohio University Heritage College of Osteopathic Medicine in Athens, Ohio. He was awarded the Ohio University Presidential Research Scholar Award and is the Chang Professor of Paleontology. He received degrees from Cornell University, the University of Kansas, and the Johns Hopkins University School of Medicine. An important aspect of this research is "fleshing out" extinct dinosaurs and their kin with the soft tissues not normally preserved as fossils. Witmer has received numerous National Science Foundation grants, and has published articles in Science, Nature, and many in other technical journals.
![]()
APPENDIX 1
FIGURE A1. Plot of superellipse exponents k (x-axis) against superellipse correction factors Cm (cross-sectional areas, mass, and the contribution of a frustrum's point mass to I of an entire body) and CI (for an individual frustrum's I) relative to an ellipse (y-axis). The polynomials enable area calculations with exponents of greater than one significant figure (Table A1).
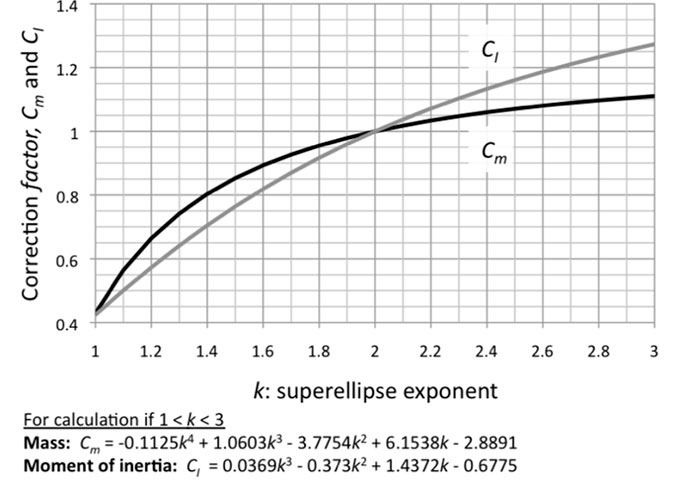
TABLE A1. Superellipse exponents (k) and coefficients for determining mass (Cmass) and mass moment of inertia (CI) relative to these quantities for an elliptical frustrum (k=2.0). Cmass is for conversion of both mass and the contribution of a frustrum's point mass to I of a body part from its center of rotation. CI is for conversions of Ix,y,z for any individual frustrum. The inverse of a coefficient gives mass or I for an ellipse if the quantity is known for a shape with another exponent k.
|
Exponent k |
Superellipse: |
Superellipse: |
|
Cmass |
CI |
|
|
1 |
0.4292 |
0.4244 |
|
1.1 |
0.5644 |
0.5006 |
|
1.2 |
0.6641 |
0.5731 |
|
1.3 |
0.7417 |
0.6412 |
|
1.4 |
0.8032 |
0.7048 |
|
1.5 |
0.8527 |
0.7639 |
|
1.6 |
0.8931 |
0.8188 |
|
1.7 |
0.9265 |
0.8695 |
|
1.8 |
0.9551 |
0.9164 |
|
1.9 |
0.9789 |
0.9598 |
|
2 |
1.0000 |
1.0000 |
|
2.1 |
1.0177 |
1.0372 |
|
2.2 |
1.0338 |
1.0716 |
|
2.3 |
1.0475 |
1.1036 |
|
2.4 |
1.0599 |
1.1333 |
|
2.5 |
1.0705 |
1.1609 |
|
2.6 |
1.0805 |
1.1866 |
|
2.7 |
1.0894 |
1.2105 |
|
2.8 |
1.0972 |
1.2328 |
|
2.9 |
1.1041 |
1.2537 |
|
3 |
1.1108 |
1.2732 |
APPENDIX 2.
Derivation of mass moment of inertia I for super-elliptical frustra
Solid Edge and other modeling software calculate inertial properties (mass, center of mass, and mass moment of inertia). The geometry for these properties will be especially accurate with NURBs ellipsoids deformed to drape over a skeleton (Mallison, 2010, 2011), for example, as in an animal's thoracic region. For a model with non-deformed ellipsoid cross sections, it is useful to estimate how differing cross-sectional shapes would affect mass m and mass moments of inertia I about orthogonal axes.
Symmetrical, curved cross sections, called super-ellipses, have shapes described by equation (5).
5) 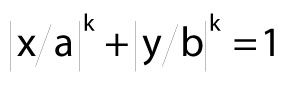
Here, x and y are variables, a and b are semi-major and semi-minor axes, and exponent k governs the shape's curvature. In an ellipse, k=2.
For an object with superelliptical cross sections, the following equation gives mass moment of inertia about a vertical axis y, with n segments (each i), and radii from dorsal to ventral (DV) and lateral to medial (LM).
6) 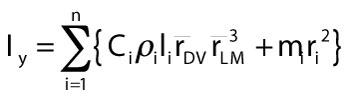
A given segment's density is 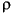 i , its length is li, and
i , its length is li, and ![]() and
and ![]() are respective averages of dorsoventral and mediolateral radii of the segment's anterior and posterior faces. The distance ri is the radius from the center of rotation of a body to the center of mass mi of segment i. Critically, C is a unique constant for a given superelliptical cross section of exponent k from equation 5 (as long as k is the same for front and back cross sections).
are respective averages of dorsoventral and mediolateral radii of the segment's anterior and posterior faces. The distance ri is the radius from the center of rotation of a body to the center of mass mi of segment i. Critically, C is a unique constant for a given superelliptical cross section of exponent k from equation 5 (as long as k is the same for front and back cross sections).
Fmax for a superellipse, and hence for I and m for objects with superelliptical sections, can be calculated using exponent k. Mosen (2009) provides a general equation for Fmax (although not for I or m), using the inverse of k. The equation becomes simpler when k is calculated and substituted algebraically.
7) 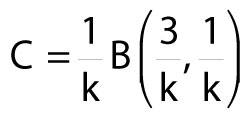
B is a beta function incorporating gamma functions defined as
8) 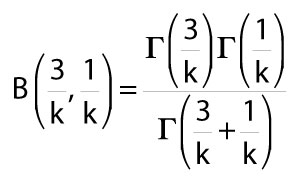
Substituting all terms and expanding equation 3, we obtain mass moment of inertia of an individual superellipse-based frustrum i about a vertical axis.
9) 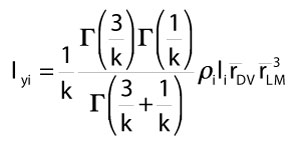
Mass and Iy vary predicably with the exponent used to define each superellipse cross section, and can be calculated by multiplying the ellipse values by a correction factor. Table A1 presents correction factors for superelipse-section frustra of varying exponents k, including that of an ellipse (k=2). Figure A1 plots these coefficients, and fitted polynomials that enable calculation of areas with exponents of higher significant figures. Common cross-sectional shapes for terrestrial vertebrates, with exponents of 2.3–2.5 (Motani 2001), result in masses 5–7% greater than for elliptical cross sections. This discrepancy supports Motani's (2001) findings that elliptical cross sections substantially underestimate body volume. I y of individual frustra increase more rapidly than mass as exponents exceed k=2, from 10–16% greater as k ranges from 2.3 to 2.5.
APPENDIX 3.
Congruent axes for joint markers in MSC Adams.
Joint markers on different bodies in Adams must be coincident. Aligning their positions, coordinate axes and axis orientations requires four steps.
1. Right-click on the joint and obtain "Info". This dialog box identifies the i and j markers.
2. Copy the angles of the i marker's global axis orientation.
3. Right-click the j marker, and select "Modify".
4. Paste the i marker's angles in place of the listed j marker's.
TABLE 1. Centers of mass of neck segments with varying tracheal diameters, and a head with a uniform assumed density and with air spaces. The dimensions are relative to the centers of the model's coordinate system. Theoretical models with no air spaces are designated Solid.
| Solid | Tracheal diameter | |||||||||||
| 6.768 cm | 4 cm | |||||||||||
| Neck | x | y | z | x | y | z | x | Y | z | |||
| C9 | 9.239 | 507.007 | -532.839 | 9.243 | 506.981 | -524.370 | 9.241 | 506.998 | -529.694 | |||
| C8 | 9.484 | 611.316 | -476.928 | 9.446 | 611.329 | -467.692 | 9.472 | 611.320 | -473.537 | |||
| C7 | 9.375 | 708.540 | -420.619 | 9.372 | 708.534 | -411.045 | 9.374 | 708.538 | -417.114 | |||
| C6 | 8.743 | 792.622 | -377.677 | 8.720 | 792.606 | -367.916 | 8.735 | 792.616 | -374.124 | |||
| C5 | 8.161 | 872.473 | -351.192 | 8.163 | 872.476 | -341.086 | 8.161 | 872.474 | -347.503 | |||
| C4 | 8.998 | 948.314 | -337.605 | 9.048 | 948.316 | -327.250 | 9.014 | 948.315 | -333.842 | |||
| C3 | 9.515 | 1025.218 | -330.166 | 9.513 | 1025.215 | -326.310 | 9.513 | 1025.215 | -326.310 | |||
| C2-1 | 11.729 | 1103.845 | -328.743 | 11.520 | 1103.238 | -314.045 | 11.655 | 1103.614 | -323.328 | |||
| Solid | Air spaces | |||||||||||
| Head | x | y | z | x | y | z | ||||||
| Head | 11.040 | 1372.946 | -344.703 | 11.100 | 1356.158 | -347.813 | ||||||
TABLE 2. Inertial properties of neck divisions and the head of Allosaurus, estimated assuming no air spaces and the density αtissue=1060 kg/m^3 (that of muscle). For neck segments, Ixx is about a vertical x axis and primarily resists lateroflexion (yaw). Iyy is about a longitudinal y axis and resists roll. Izz is about the transverse z axis and resists dorsoventral movements (pitch). Note that segment C2-1 tapers anteriorly and behaves differently than other segments. For the head, the x axis is horizontal and Ixx resists pitch; the y axis is vertical and Iyy resists lateroflexion; and the z axis is longitudinal and Izz resists roll.
| Segment | Vol (m^3) |
Mass (kg) |
Mass moments of inertia (kg m^2) | |||||
| I xx | I yy | I zz | I xy | I xz | I yz | |||
| C9 | 0.006359 | 6.741 | 0.02926 | 0.07513 | 0.06812 | -0.01654 | -0.000007 | 0.000036 |
| C8 | 0.006403 | 6.787 | 0.02927 | 0.07689 | 0.07158 | -0.01796 | -0.000002 | -0.000005 |
| C7 | 0.005565 | 5.899 | 0.02308 | 0.06947 | 0.06425 | -0.01603 | 0.000156 | -0.000048 |
| C6 | 0.004675 | 4.955 | 0.01739 | 0.05716 | 0.05148 | -0.01206 | 0.000161 | 0.000079 |
| C5 | 0.004786 | 5.074 | 0.01764 | 0.05782 | 0.05268 | -0.01232 | -0.000027 | -0.000007 |
| C4 | 0.004177 | 4.428 | 0.01441 | 0.05228 | 0.04768 | -0.01121 | 0.00001 | 0.000043 |
| C3 | 0.004905 | 5.200 | 0.01700 | 0.06200 | 0.05800 | -0.01300 | -0.000015 | -0.000200 |
| C2-1 | 0.003422 | 3.627 | 0.00900 | 0.03900 | 0.03900 | -0.00900 | 0.000037 | 0.000142 |
| Head | 0.026120 | 27.69 | 0.92420 | 0.34680 | 1.16300 | 0.22170 | -0.000522 | -0.001461 |
TABLE 3. Volumes and inertial properties of the head of Allosaurus, calculated for varying tissue densities. As in Table 2 values for the head, the x axis is horizontal and Ixx resists pitch; the y axis is vertical and Iyy resists lateroflexion; and the z axis is longitudinal and Izz resists roll.
| ρtissue (kg/m^3) |
Vol (m^3) |
Mass (kg) |
Mass moment of inertia (kg m^2) | |||||
| I xx | I yy | I zz | I xy | I xz | I yz | |||
| 1128 | 0.022 | 25.16 | 0.8425 | 0.3490 | 1.0810 | 0.2127 | -0.00051 | -0.00153 |
| 1231 | 0.022 | 27.46 | 0.9197 | 0.3809 | 1.1801 | 0.2322 | -0.00056 | -0.00167 |
| 1321 | 0.022 | 29.48 | 0.9873 | 0.4089 | 1.2668 | 0.2492 | -0.00060 | -0.00179 |
| 1347 | 0.022 | 30.06 | 1.0066 | 0.4169 | 1.2916 | 0.2541 | -0.00061 | -0.00183 |
| 1373 | 0.022 | 30.64 | 1.0259 | 0.4249 | 1.3163 | 0.2590 | -0.00063 | -0.00186 |
TABLE 4. Inertial properties of Allosaurus neck segments, estimated with average tracheal diameters of 6.768 cm (from a regression for all birds), and 4 cm (regression for chickens and relatives; Hinds and Calder, 1971). Mass moments of inertia are as in Table 2 values for neck segments. Ixx is about a vertical x axis and primarily resists lateroflexion (yaw). Iyy is about a longitudinal y axis and resists roll. Izz is about the transverse z axis and resists dorsoventral movements (pitch).
|
Trachea |
Segment | Vol (m^3) |
Mass |
Mass moment of inertia (kg m^2) |
|||||
|
I xx |
I yy |
I zz |
I xy |
I xz |
I yz |
||||
| 6.768 cm | C9 | 0.00599 | 6.349 | 0.0282 | 0.0676 | 0.0598 | -0.1451 | -3.00E-06 | 3.40E-05 |
| C8 | 0.00603 | 6.388 | 0.0281 | 0.0680 | 0.0618 | -0.0155 | -3.90E-05 | 5.00E-06 | |
| C7 | 0.00524 | 5.554 | 0.0221 | 0.0611 | 0.0551 | -0.0137 | 1.54E-04 | -4.70E-05 | |
| C6 | 0.00439 | 4.658 | 0.0170 | 0.0498 | 0.0438 | -0.0107 | 1.43E-04 | -7.60E-05 | |
| C5 | 0.00449 | 4.764 | 0.0176 | 0.0578 | 0.0527 | -0.0123 | 2.70E-05 | -7.00E-06 | |
| C4 | 0.00392 | 4.159 | 0.0137 | 0.0453 | 0.0401 | -0.0094 | 4.40E-05 | 3.30E-05 | |
| C3 | 0.00480 | 5.088 | 0.0165 | 0.0532 | 0.0483 | -0.0108 | -1.90E-05 | -1.80E-05 | |
| C2-1 | 0.00311 | 3.302 | 0.0080 | 0.0313 | 0.0310 | -0.0070 | -7.20E-05 | 1.61E-03 | |
| Vol (m3) |
Mass (kg) |
I xx | I yy | I zz | I xy | I xz | I yz | ||
| 4 cm | C9 | 0.00623 | 6.604 | 0.0289 | 0.0721 | 0.0647 | -0.0157 | -5.000E-06 | 3.50E-05 |
| C8 | 0.00627 | 6.647 | 0.0289 | 0.0734 | 0.0677 | -0.0170 | -1.500E-05 | -2.00E-06 | |
| C7 | 0.00545 | 5.779 | 0.0221 | 0.0611 | 0.0551 | -0.0137 | 1.540E-03 | -4.70E-05 | |
| C6 | 0.00458 | 4.852 | 0.0174 | 0.0541 | 0.0485 | -0.0118 | 1.540E-04 | -8.00E-05 | |
| C5 | 0.00468 | 4.965 | 0.0174 | 0.0548 | 0.0494 | -0.0115 | 2.800E-05 | -7.00E-06 | |
| C4 | 0.00409 | 4.334 | 0.0142 | 0.0496 | 0.0447 | -0.0105 | 2.200E-05 | 3.90E-05 | |
| C3 | 0.00480 | 5.088 | 0.0171 | 0.0584 | 0.0539 | -0.0122 | -1.600E-05 | -2.00E-05 | |
| C2-1 | 0.00331 | 3.511 | 0.0084 | 0.0360 | 0.0360 | -0.0080 | -4.000E-06 | 1.49E-04 | |
TABLE 5. Dimensions, baseline specific tension ST of 55 N/cm^2 (O'Brien et al., 2010), and Fmax of reconstructed muscles of Allosaurus. Abbreviations: MTCP=musculus transversospinalis capitis; MTCR=musculus transversospinalis cervicis; MLCS=musculus longissimus capitis superficialis; MLCP= musculus longissimus capitits profundus; MRCA=musculus rectus capitis anterior/ventralis.
| Semi-major (cm) |
Semi-minor (cm) |
Area (cm^2) |
Area (cm^2) |
ST (N/cm^2) |
Fmax (N) |
||||
| Muscle | baseline | robust | baseline | robust | baseline | robust | baseline | robust | |
| MTCP | 3.513 | 3.865 | 2.550 | 2.805 | 30.13 | 36.46 | 55 | 1657 | 2005 |
| MTCR | 2.929 | 3.222 | 2.366 | 2.603 | 23.31 | 28.21 | 55 | 1282 | 1551 |
| MLCS | 2.996 | 3.295 | 3.267 | 3.593 | 32.91 | 39.82 | 55 | 1810 | 2190 |
| MLCP | 4.531 | 4.984 | 1.753 | 1.928 | 26.70 | 32.31 | 55 | 1469 | 1777 |
| MRCA | 4.016 | 4.418 | 1.624 | 1.786 | 21.93 | 26.54 | 55 | 1206 | 1460 |
FIGURE 1. Lateral and dorsal profiles of Allosaurus (MOR 693) used for 3D reconstructions. Air spaces are color coded as transparent objects; colors may appear darker where the rendering of the bone is darker. Lines labeled as C represent cervical (neck) segments associated with respective cervical vertebrae, as S represent divisions of the skull and head. E=ear, C=cervical, S=skull.
Specific landmarks: E1 and E2, intermediate segments of the middle ear cavity. C2-1, posterior of these vertebrae and the skull, except the retroarticular process. S1, top of parietals. S2, anterior edge of visible jaw muscles. S3, posterior edge of orbit. S4, posterior edge of lacrimal. S5, anterior edge of lacrimal's jugal ramus, posterior edge of antorbital sinus. S8, anterior extent of antorbital sinus. S10, anterior extent of bony nostril.
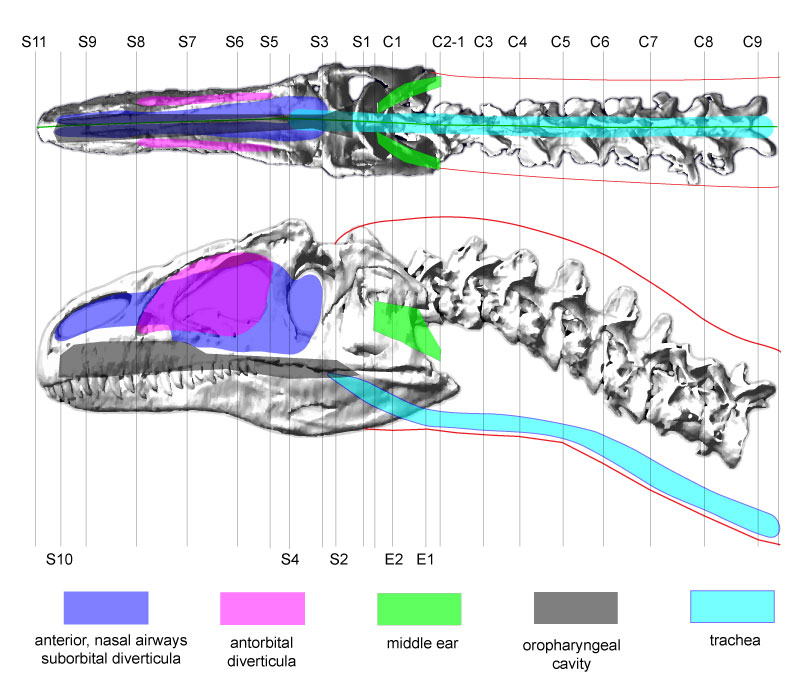
FIGURE 2. The dynamics model of Allosaurus (MOR 693), visualized with CT skeletal data from Adams registered with the Solid Edge model of its fleshed-out geometry. Compared with Figure 1, lofting in Solid Edge has caused a bulge behind the parietals. TD=tracheal diameter; note the cutout in the anterior neck segment at TD=7 cm (as in Figure 7). The interior, purple objects are air spaces. The blue sphere is at the COM of the head, and yellow spheres and coordinate systems are for centers of mass for neck segments. The Z over each neck COM designates the transverse, Z axis of Solid Edge's coordinate system for the COM.
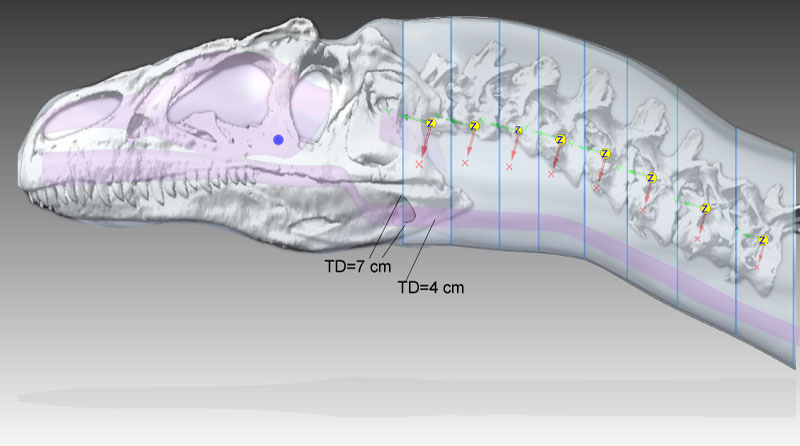
FIGURE 3. Dorsal oblique view of external geometry of the head and neck of Allosaurus, showing the lofted cutout in the head segment to accommodate the segment for cervical vertebrae 1 and 2 (C1–2). Elements of the model's geometry were positioned relative to the origin and axes of the global coordinate system (lower right). The colored sphere indicates the head's center of mass.
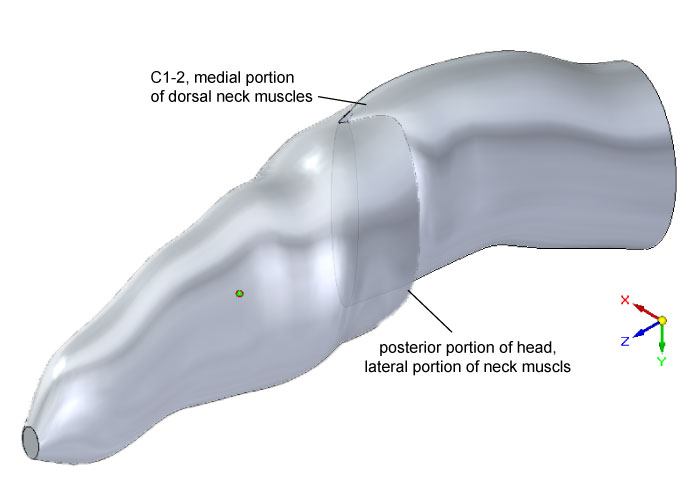
FIGURE 4. (1) Lateral view of the modeled head geometry of Allosaurus depicting air spaces in place; the antorbital diverticulum (air sac) is superficial in position and in a darker color. The small sphere locates the COM of the remaining head tissue. (2) Air spaces within the head of Allosaurus. The middle ear space (pharyngotympanic sinus) extends from the eardrum to the braincase. The constricted laryngopharynx/anterior trachea is an artifact of the lofting procedure in Solid Edge.
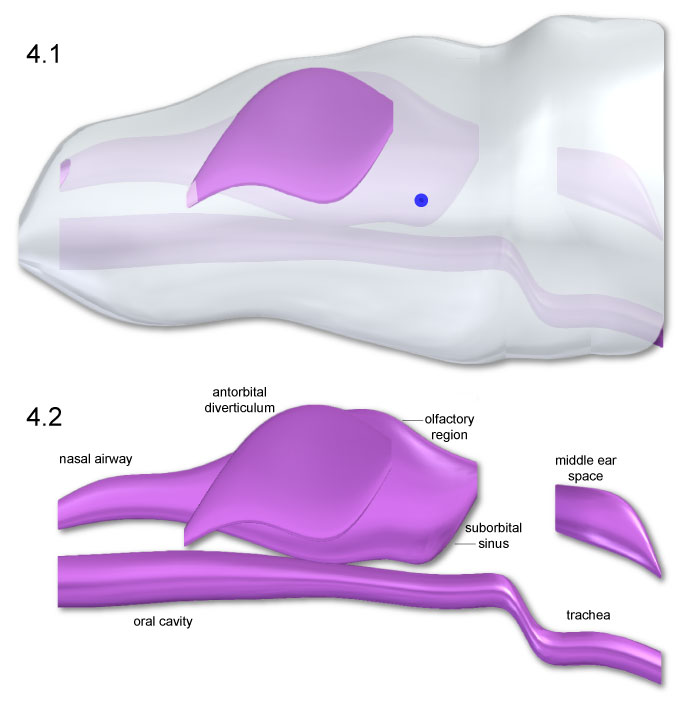
FIGURE 5. Dorsal (1 and 2) and ventral (3 and 4) views of Allosaurus head and air space geometry. The blue spheres locate the head COM Slight dorsomedial inclination of the antorbital diverticula (2 and 3) was necessary to enclose the structures within the head.
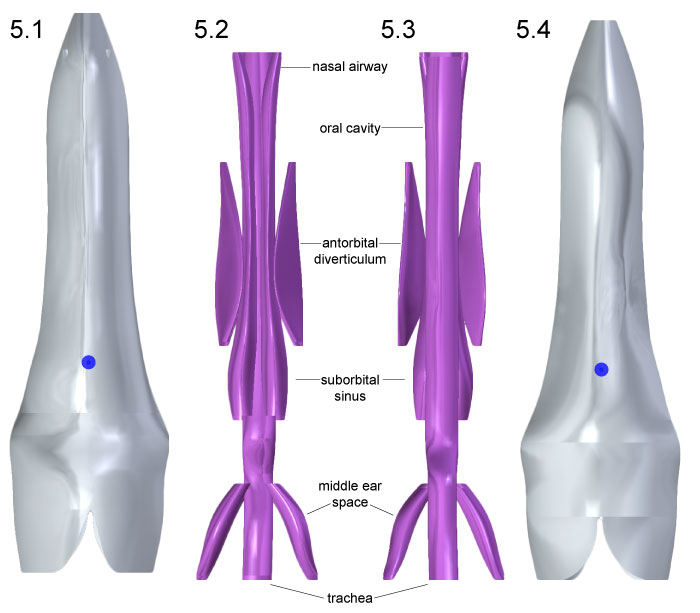
FIGURE 6. Head geometry of Allosaurus is shown in anterior (1) and posterior (2) views, with blue spheres representing centers of mass for head tissues. Air spaces in the same respective views (3, 4) depict slight medial inclination of the antorbital diverticula.
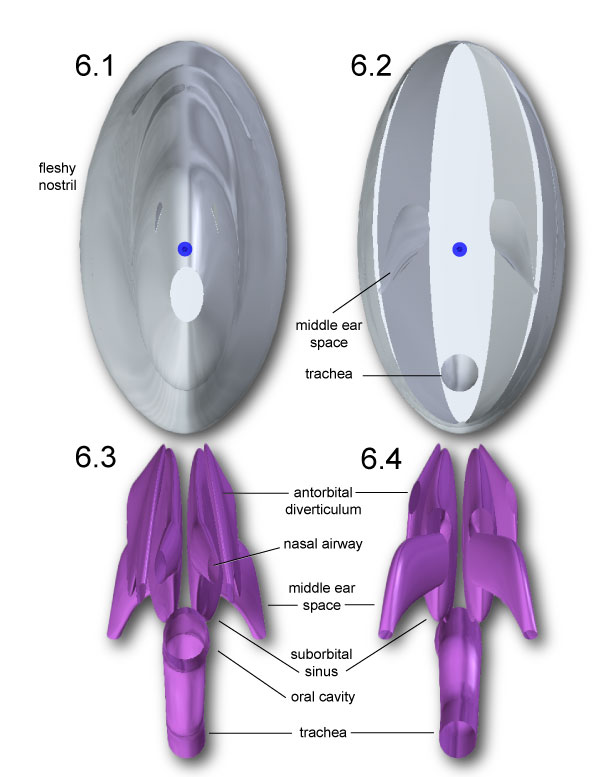
FIGURE 7. Centers of mass (yellow spheres) for neck segments of Allosaurus, determined for tracheal diameters of 6.768 cm (1) and 4 cm (2). The COM for each segment is slightly more ventral with 4 cm trachea. The 6.768 cm trachea scallops out the anterior of segment C1-2 (1) at the left of the model. Note that the axes (x,y,z) are equivalent to (y,z,x) in the Adams model and Table 2,Table 3, and Table 4.
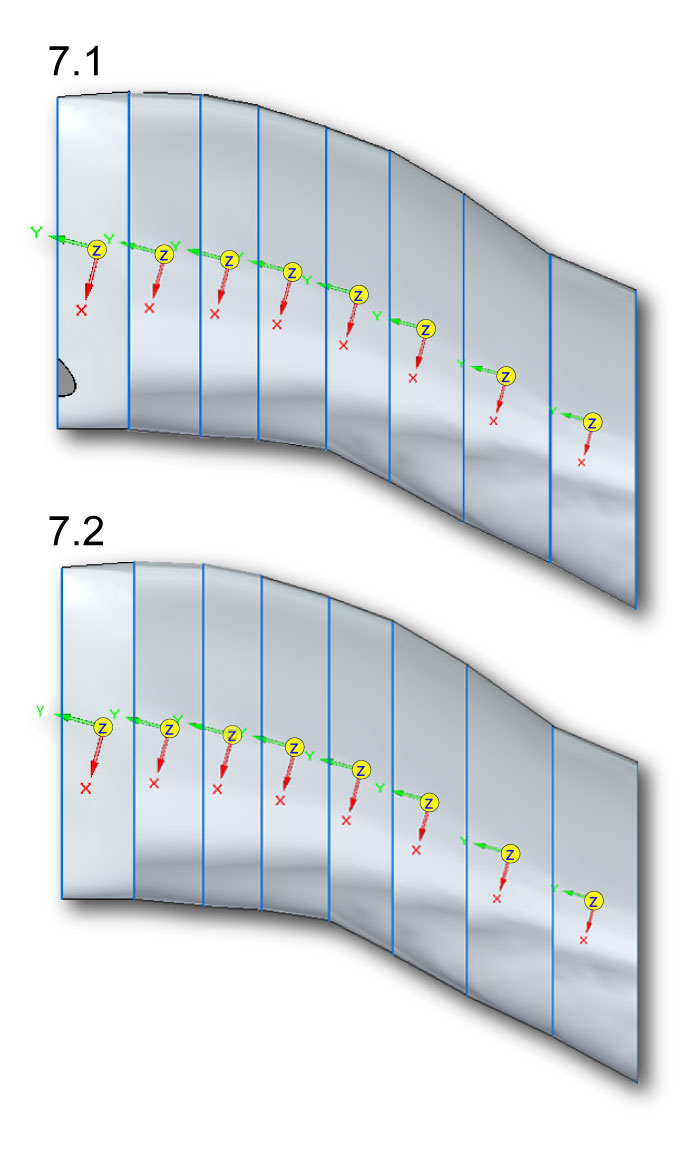
FIGURE 8. Ventroflexor insertions on the occiput of Allosaurus (MOR 693). Abbreviations:
MLCS=musculus longissimus capitis superficialis. MLCP=musculus longissimus capitis profundus. MRCA=m. rectus capitis anterior/ventralis. CR=center of rotation, on the occipital condyle.
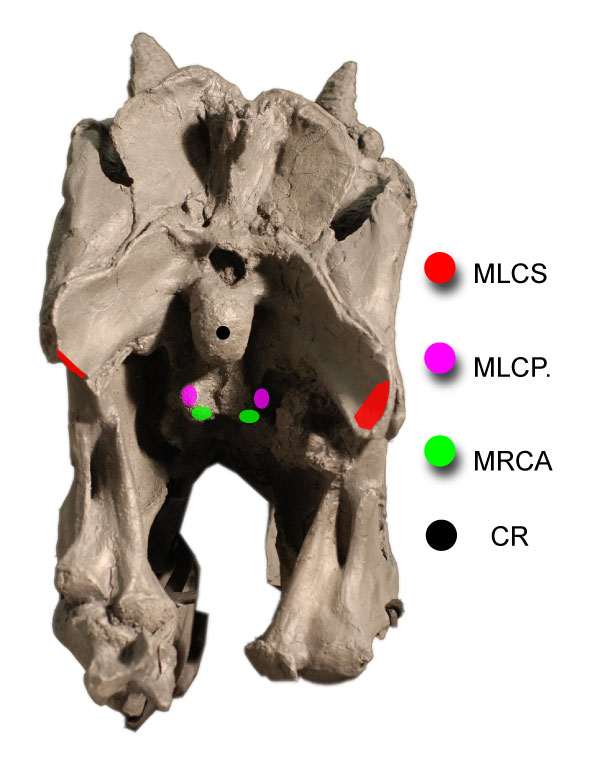
FIGURE 9. Reconstruction of head ventroflexors of Allosaurus (MOR 693) in lateral (1, 3) and dorsal (2, 4) views, with abbreviations from Figure 8. In (2) and (4), the ventroflexors m. longissimus capitis profundus (MLCP) and m. rectus capitis anterior/ventralis (MRCA) are ventral to the vertebrae.
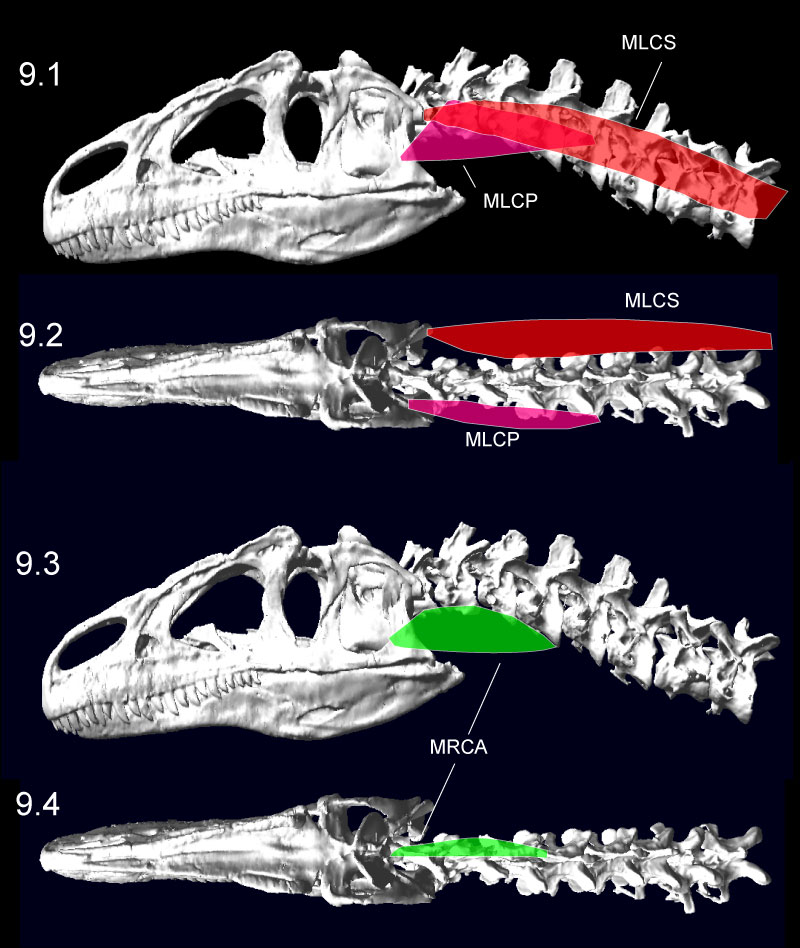
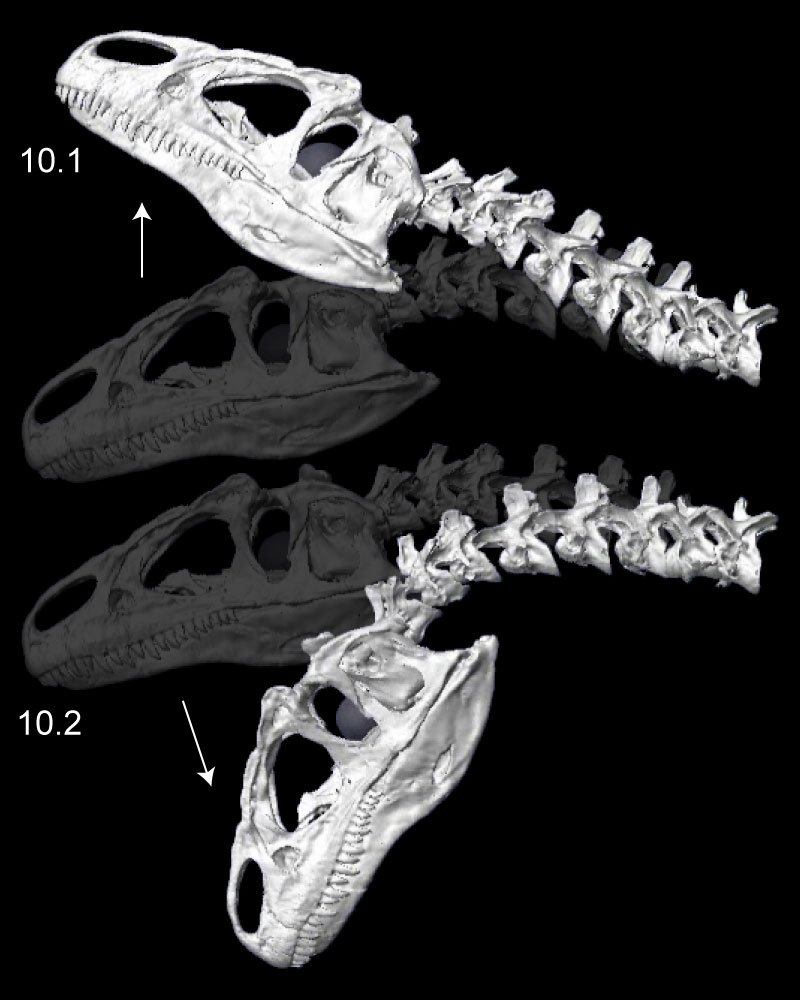
FIGURE 10. Dorsiflexion (1) and ventroflexion (2) of the Allosaurus (MOR 693) model in MSC Adams, minimizing disarticulation of the zygapophyses. The head could ventroflex at a steeper angle than simulated here (Figure 13). The transparent sphere within the cranium was used to position skull center of mass. Click on image to see animation.
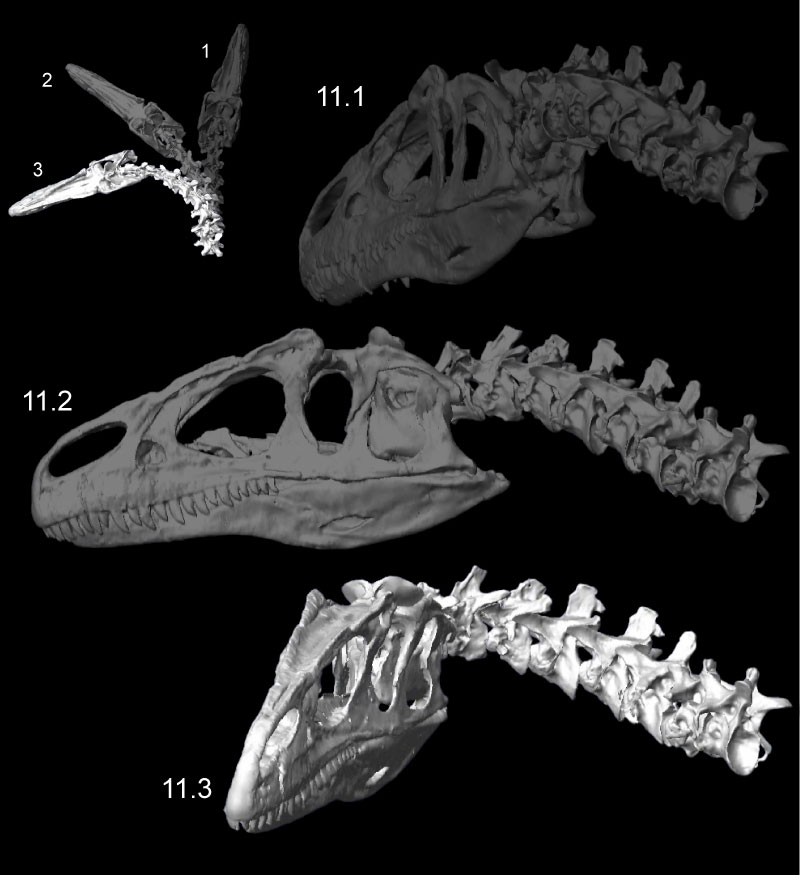
FIGURE 11. Left lateroflexion of the head and neck of Allosaurus (MOR 693), with slight right-turned (1), intermediate (2), and fully lateroflexed (3) poses. In the initial pose (1), the head and all cervical vertebrae are in posterolateral view. Note relative rotation and reasonable overlap of zygapophyses in all poses.
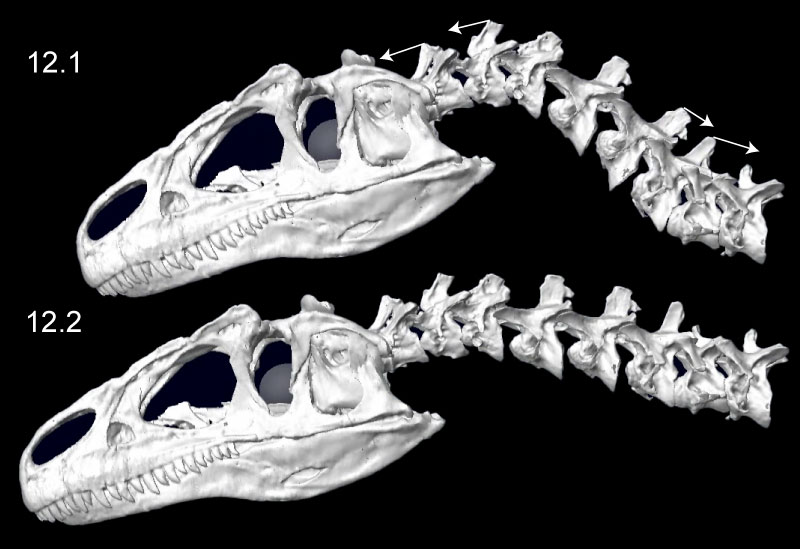
FIGURE 12. Retraction (1) and protraction (2) of the head and neck of Allosaurus (MOR 693), from kinematic simulations. The white arrows at neural spines show primary angular movements of vertebrae in retraction. The transparent sphere within the cranium was used to position skull center of mass. Click on image to see animation.
FIGURE 13. Ventroflexion simulated on the skull of Allosaurus (MOR 693). The rows indicate simulation time. The columns are for the initial position of each simulation, endpoints for gravity acting alone, m. longissimus capitis superficialis acting alone, and for all ventroflexors acting together. The coordinate axes (lower left) are as in Table 3, for x (transverse), y (dorsoventral), and z (anteroposterior) directions; movement about these axes are for pitch (simulated here), yaw, and roll, respectively. The white arrows indicate displacement magnitudes of the tip of the snout from the initial position in the x direction. Muscles are modeled as line-of-sight tensile forces (thin red lines) from origin to insertion.
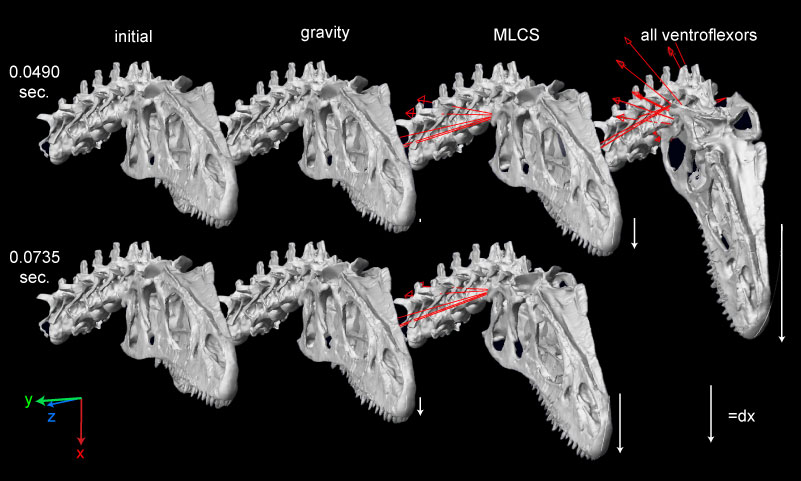
FIGURE 14. Ventroflexive movement of the anterior tip of the cranium of Allosaurus, plotted against time and including the point's vertical position (dx). 1 and 2 plot linear (acm, vcm) and angular ( cm,
cm,  cm) accelerations and velocities with all ventroflexors activated. 3 and 4 plot the same quantities with contraction of m. longissimus capitis superficialis (MLCS).
cm) accelerations and velocities with all ventroflexors activated. 3 and 4 plot the same quantities with contraction of m. longissimus capitis superficialis (MLCS).
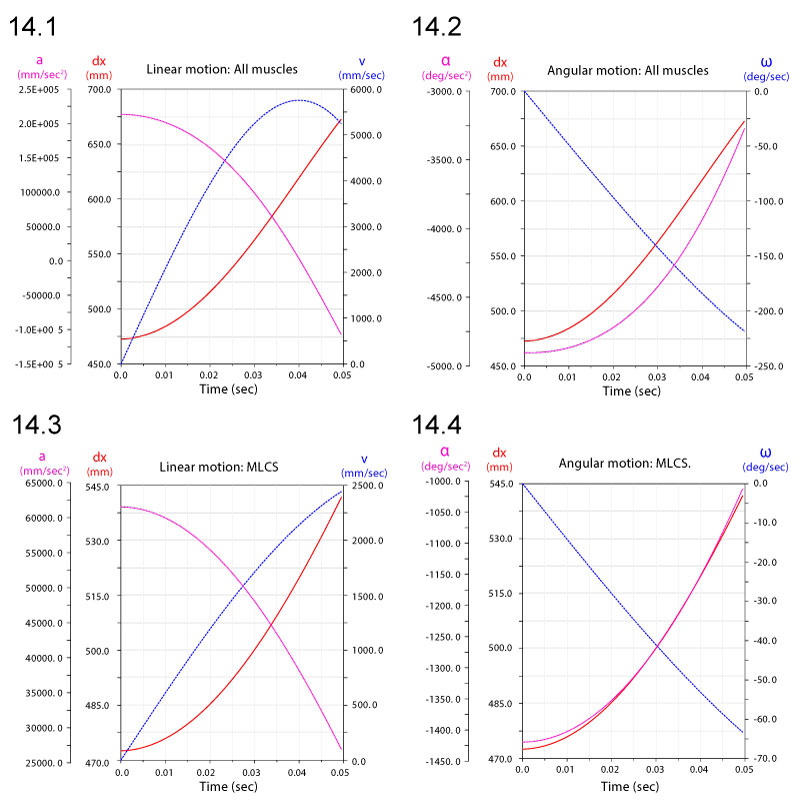
FIGURE 15. Linear displacements dx (1), velocities v (2), and accelerations a (3) of a point at the anterior tip of the premaxilla of Allosaurus. Subscripts refer to simulations with gravity alone, all ventroflexors (all), and just m. longissimus capitis superficialis (MLCS).
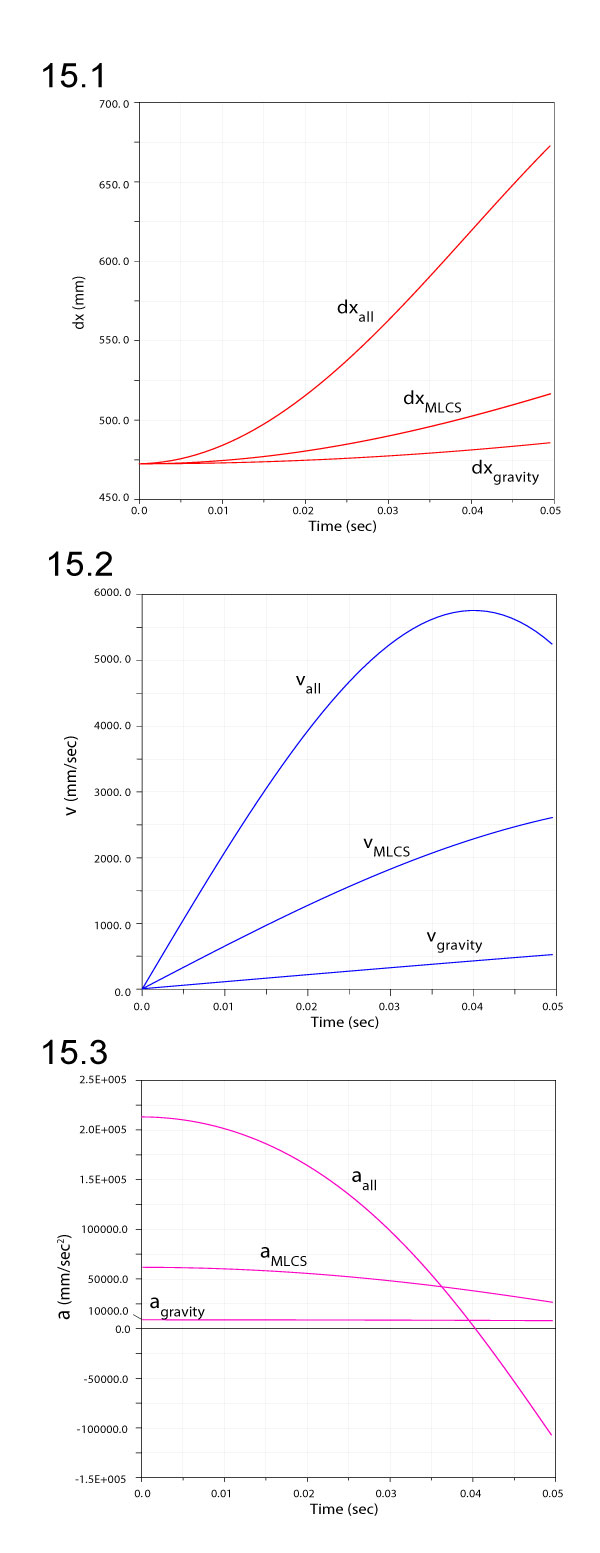
FIGURE 16. Comparison of angular velocities  (1) and accelerations
(1) and accelerations  (2) for ventroflexion simulations with gravity only, gravity plus m. longissimus capitis superficialis (MLCS), and all ventroflexors (all) active.
(2) for ventroflexion simulations with gravity only, gravity plus m. longissimus capitis superficialis (MLCS), and all ventroflexors (all) active.
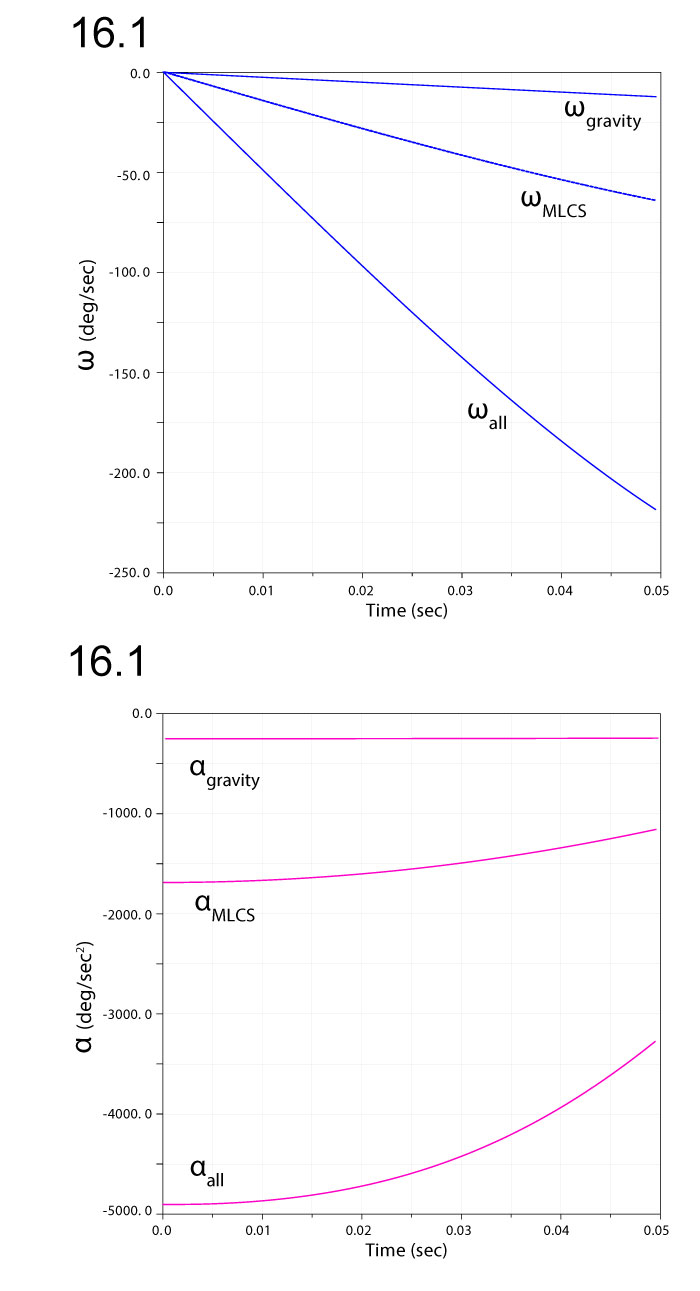
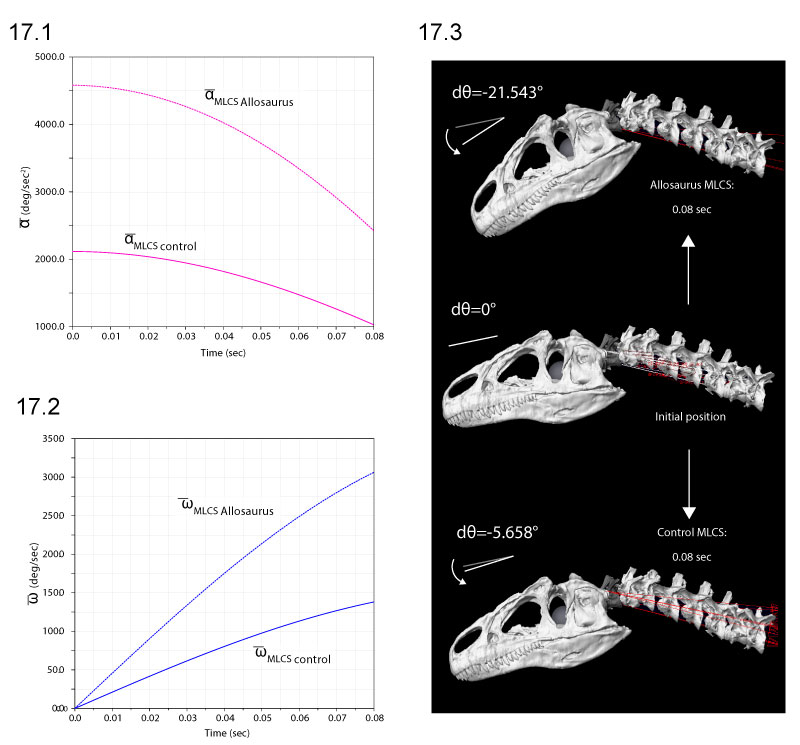
FIGURE 17. Comparison of ventroflexive angular accelerations  (1), velocities
(1), velocities  (2), and displacements dθ (3), for two different reconstructions of m. longissimus capitis superficialis (MLCS). Absolute values of
(2), and displacements dθ (3), for two different reconstructions of m. longissimus capitis superficialis (MLCS). Absolute values of  and ω enable comparisons of relative magnitudes. The ventral insertion of the muscle in of Allosaurus imparts over twice the
and ω enable comparisons of relative magnitudes. The ventral insertion of the muscle in of Allosaurus imparts over twice the  (and torque) of the control throughout the 0.08 sec of the simulation (1), and reaches 3.8 times the angular displacement (3).
(and torque) of the control throughout the 0.08 sec of the simulation (1), and reaches 3.8 times the angular displacement (3).
Multibody dynamics model of head and neck function in Allosaurus (Dinosauria, Theropoda)
Plain Language Abstract
The Jurassic Allosaurus is an iconic predatory dinosaur found in the American West and Portugal that, for over a century, has been second only to Tyrannosaurus rex as a somewhat smaller, three-clawed archetype of dinosaurian carnivory. Allosaurus stands out among large theropod dinosaurs for its abundance in the fossil record, but less widely appreciated is the sinuosity of its neck. Allosaurus exemplifies its eponymous group of dinosaurs, the Allosauroidea, with classic, flexible ball-and-socket joints between its neck vertebrae.
Yet even stranger than allosauroid relatives like the enormous Giganotosaurus and powerful Acrocanthosaurus, Allosaurus appears to have been uniquely equipped to drive its head downwards. Robert Bakker documented unusual attachments for neck muscles of Allosaurus, which in crocodilians turn the head but in Allosaurus also have leverage for ventroflexion (downwards, nodding movements). Emily Rayfield showed that the cranium (upper part of the skull) of Allosaurus was stronger than expected from its estimated bite force. Perhaps moving the head down and back assisted Allosaurus in driving its upper teeth into flesh.
To investigate ventroflexion and other neck movements in Allosaurus, we use a relatively new method in biology called multibody dynamics. From CT scans of the head and neck of an Allosaurus (the same specimen that Emily Rayfield used), we built a fleshed-out digital model that has anatomical and physical properties (joints, muscle forces, and rotational inertias) for simulating motions of attack, feeding, or just looking around. Our model includes detailed anatomy of air-filled pneumatic diverticula, like living balloons connected to the nasal cavity and middle ear in bird and crocodilians, which hollowed out the skull. Since we don’t know things like the size of the windpipe, the density of bone in Allosaurus’s skull, or the exact size and shape of some muscles, we vary those values to obtain a biologically realistic range of Allosaurus head accelerations.
Despite the complexity of joints in the neck of Allosaurus, the model performed smoothly to reveal large ranges of motion for moving the head in nearly every direction. The muscle that was unusual in attaching along the side of its neck (m. longissimus capitis superficialialis) contributed at least 25% of the total acceleration for ventroflexion, supporting Bakker’s hypothesis. Yet what behaviors did this ventroflexion facilitate? Did Allosaurus strike downwards quickly—Bakker’s interpretation—or move the upper teeth into flesh more slowly, as Mauricio Antón suggests?
Our study does not support either possibility more strongly than the other, but clues from the modern relatives of Allosaurus offer a complementary alternative. Raptorial birds vary in how they eat prey. Texas falconer Manuel Carasco runs a red-tailed hawk named Dakota, a startlingly intelligent bruiser who feeds mainly with pulling motions of her head and neck. In contrast, small falcons (including merlins and kestrels), which have impressive ventroflexive muscles like those inferred for Allosaurus, hook their beak and jaws into prey and pull mainly with their legs and body. The neck muscles appear to hold the head steady as the legs do most of the work. We envision Allosaurus as being capable of similar motions, pulling flesh from prey like these small raptorial birds.
Resumen en Español
Un modelo multicuerpo para el estudio de la dinámica de la cabeza y el cuello en Allosaurus (Dinosauria, Theropoda)
Presentamos un modelo multicuerpo para el estudio de la dinámica del aparato masticador de Allosaurus, un dinosario terópodo jurásico de gran tamaño, que permite contrastar hipótesis sobre el comportamiento alimentario del animal y la influencia de los parámetros anatómicos. Hemos creado modelos de huesos, tejidos blandos y espacios llenos de aire a partir de tomografía computarizada e inferencia anatómica, que hemos usado para proveer de propiedades inerciales a la dinámica músculo-esquelética. Las variaciones en la densidad ósea tienen un efecto sorprendentemente amplio en las propiedades inerciales de la cabeza y el diámetro de la tráquea afecta intensamente a los momentos de inercia de los segmentos del cuello en los movimientos dorsoventrales, La localización ventral de la inserción del músculo longissimus capitis superficialis en Allosaurus da lugar a una aceleración en los movimientos ventroflexivos mayor del doble que la inserción lateral en el cóndilo occipital característica de casi todos los demás terópodos. Se considera, por tanto, más probable que Allosaurus se alimentara descarnando la presa mediante retracciones de la cabeza, de forma similar a las aves rapaces, que mediante sacudidas lateroflexivas como las de los cocodrilos o las inferidas para los tiranosáuridos.
Palabras clave: Dinosauria; biomecánica; alimentación; dinámica de sistemas multicuerpo; músculo
Traducción: Miguel Company
Résumé en Français
Un modèle dynamique fonctionnel multi-corps de la tête et du cou chez Allosaurus (Dinosauria, Theropoda)
Nous présentons un modèle dynamique multi-corps de l'appareil nutritif du grand théropode jurassique Allosaurus permettant de tester les hypothèses concernant le comportement alimentaire et de comment le fonctionnel est influencé par les paramètres anatomiques. Nous avons créé des modèles des os, des tissus mous, et des cavités aériennes basés sur la tomographie assistée par ordinateur (CT) et la déduction anatomique, modèles qui nous avons utilisés pour définir les propriétés d'inertie du système dynamique muscle-squelette. Les estimations de densité de l'os ont un effet étonnamment important sur les propriétés d'inertie de la tête, et le diamètre de la trachée affecte fortement les moments d'inertie des segments du cou dans les mouvements dorso-ventraux. L'insertion au niveau ventral du m. longissimus capitis superficialis chez Allosaurus transmet plus deux fois l'accélération ventro-flexive par comparaison à une insertion de référence partant du condyle latéral à occipital, cette dernière étant la position de chez presque tous les théropodes. Un style d'alimentation impliquant un dépeçage de carcasse par rétraction de la tête de type oiseau-raptor chez Allosaurus est plus probable qu'un mouvement de secousses latero-flexives, tels qu'observé chez les crocodiliens et suggérés pour les tyrannosauridés.
Most clés: Dinosauria; biomécanique; alimentation; dynamique multi-corps; muscle
Translator: Olivier Maridet
Deutsche Zusammenfassung
Mehrkörperdynamikmodell der Kopf-und Halsfunktion von Allosaurus (Dinosauria, Theropoda)
Wir stellen ein Mehrkörperdynamikmodell des Nahrungsaufnahmeapparates des großen jurassischen Theropoden Allosaurus vor, welches uns erlaubt die Hypothese über die Fressgewohnheiten des Tieres zu testen und wie anatomische Parameter die Funktion beeinflussen. Wir erstellten CT- und anatomisch-Inferenz-basierte Modelle von Knochen, Weichteilen und Luftzwischenräumen, die wir nutzen um die Trägheit der Dynamik des Bewegungsapparates zu bestimmen. Kalkulationen der Knochendichte haben einen erstaunlich großen Effekt auf Trägheit bezüglich des Schädels und der Durchmesser der Luftröhre hat großen Einfluss auf die Trägheitsmomente der Halssegmente bei dorsoventralen Bewegungen. Der ventral gelegene Ansatz des m. longissimus capitis superficialis bei Allosaurus gab die ventroflexive Beschleunigung eines Proxy-Kontrollen-Ansatzes lateral zum Occipitalcondylus - der diese Position in nahezu allen anderen Tetrapoden hat - mehr als doppelt so schnell weiter. Ein Fressverhalten von Allosaurus, der Kadaver mit Vogel-Raptoren-artigem Rückziehen des Kopfes entfleischt ist wahrscheinlicher als lateroflexives Schüttelfressen, wie es bei Krokodilen vorkommt und bei Tyrannosauriden angenommen wird.
SCHLÜSSELWÖRTER: Dinosauria; Biomechanik; Fressen; Mehrkörperdynamik; Muskel
Translators: Eva Gebauer
Arabic

Translator: Ashraf M.T. Elewa
-
-
PE: An influential journal
 Palaeontologia Electronica among the most influential palaeontological journals
Palaeontologia Electronica among the most influential palaeontological journalsArticle number: 27.2.2E
July 2024





 A Review of Handbook of Paleoichthyology Volume 8a: Actinopterygii I, Palaeoniscimorpha, Stem Neopterygii, Chondrostei
A Review of Handbook of Paleoichthyology Volume 8a: Actinopterygii I, Palaeoniscimorpha, Stem Neopterygii, Chondrostei