Andrew Robert Henry Swan
School of Geography, Geology and the Environment
Faculty of Science, Engineering and Computing
Kingston University
Penrhyn Road
Kingston upon Thames, Surrey KT1 2EE
United Kingdom
swan@kingston.ac.uk

The author graduated from Imperial College, London, with a BSc in Geology in 1978, and then gained a PhD at Leeds University in 1984 on numerical analysis of Carboniferous ammonoids, supervised by Bill Ramsbottom. After a year working with Bruce Saunders at Bryn Mawr College, Pennsylvania and 3 years at University College Swansea, Wales, he gained a lectureship at his current place of work (Kingston University, London). He teaches palaeontology and statistical methods, and is currently Deputy Head of the School of Geography, Geology and the Environment.

FIGURE 1. Raup’s definition of the shell dimensions on which the equations for parameters W, D and T are derived. Based on Raup (1966).

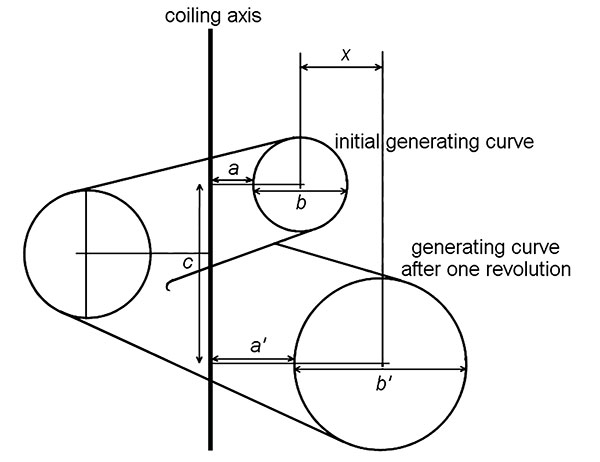
FIGURE 2. Isometric and allometric gastropods and simulations. 1, An example of a “Raupian” gastropod (Epitonium), showing isometric growth. 2, An example of a “Raupian” simulation with similar shape. 3, An example of an allometric gastropod (Megacochlea); note that there is no straight line that is tangential to the outside of all whorls. 4, A simulation using the program described here with similar shape. (Figures 2.1 and 2.3 © The Trustees of the Natural History Museum, London, reproduced from Anon, 1975, with kind permission.)

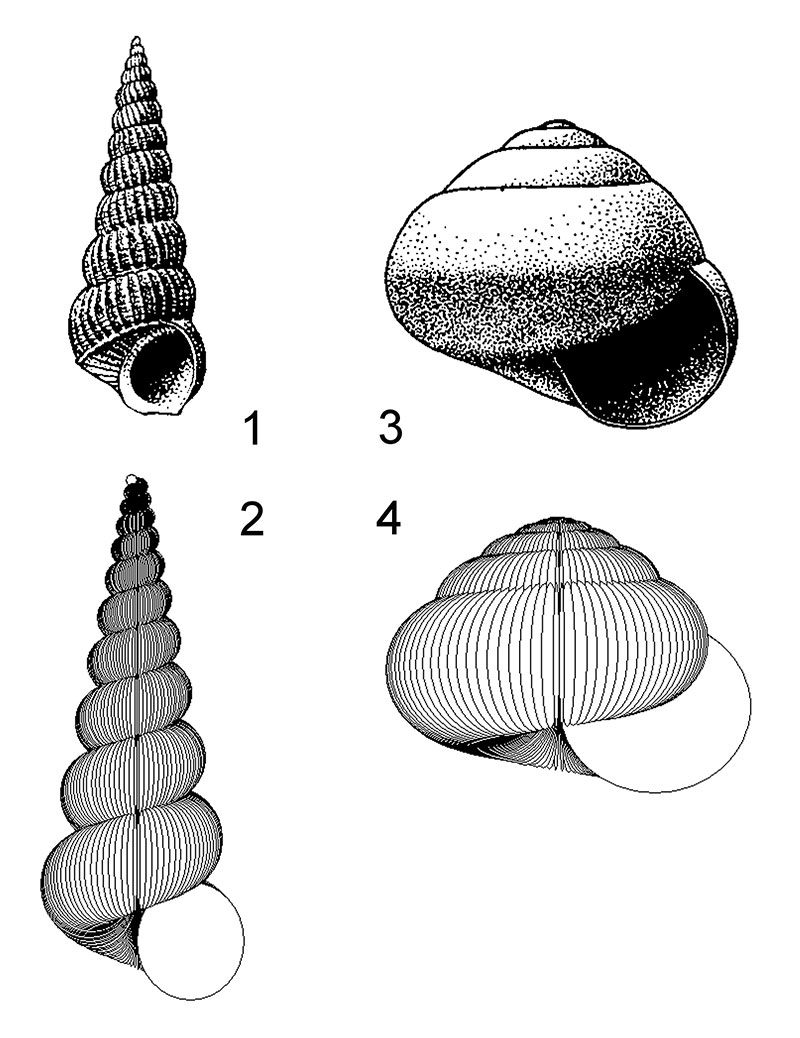
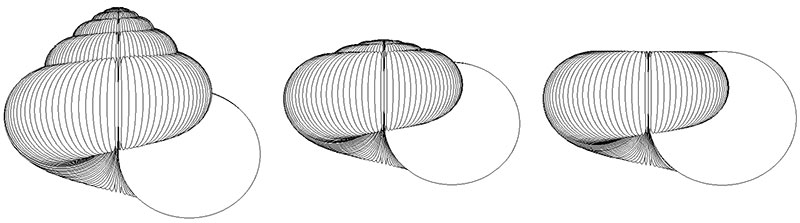
FIGURE 3. Modes of heterochronic change. The central simulation has parameters W₀ =2.5, ΔW =-0.12, D =0, S =0.8, T’₀ =0.4, ΔT’ =0.06, and has six whorls. The other four simulations show the result of one increment of each mode of heterochronic change. The two forms on the left are paedomorphic; the forms on the right are peramorphic. Note that in this case neoteny results in larger size as the ontogenetic decline in whorl expansion is reduced, and acceleration results in a smaller size for the converse reason.

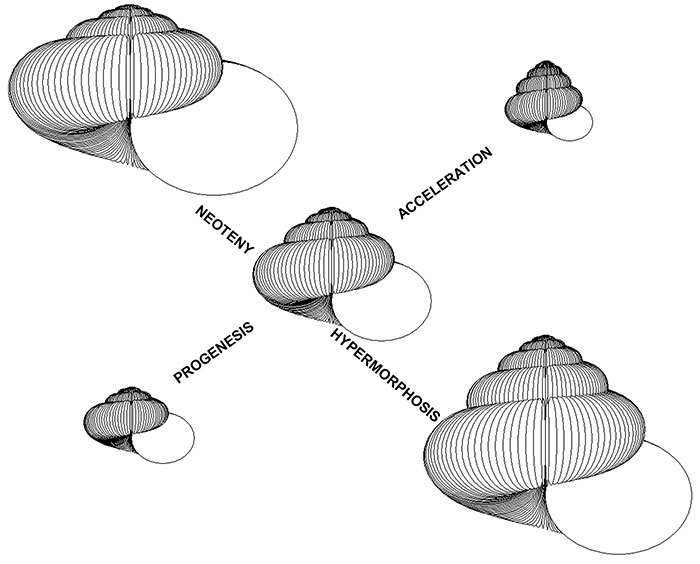
FIGURE 4. Heterochronic modelling experiment 1. The “ancestor” on the left has parameters W₀ =2.5, ΔW =-0.1, D =0, S =1, T’₀ =0, ΔT’ =0.15, and has seven whorls. It has a general shape that is common in gastropods, and especially amongst the subclass Pulmonata. The central simulation is derived from this by one increment of acceleration (relative scale x 1.5) and the simulation on the right by two increments of acceleration (relative scale x 2). The incipient reduction in whorl diameter and incipient loss of whorl-to-whorl contact is typical of some Pulmonata, such as Family Chondrinidae. Note that if Raup’s T were used, incipient reduction in whorl diameter ( W <1) would lead to reversal of the translation direction, which is nonsensical; using T ’, this is not the case.

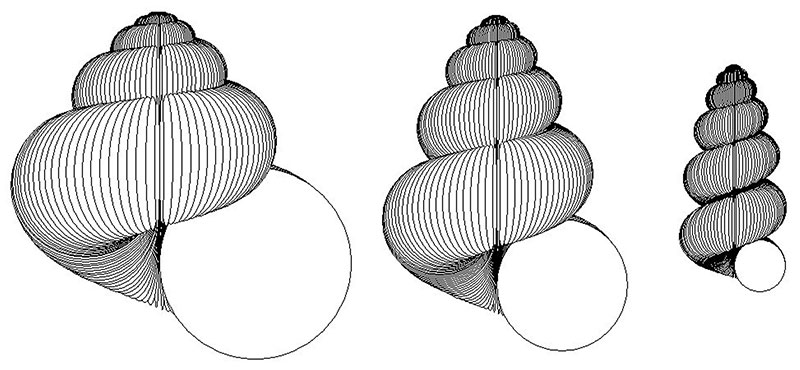
FIGURE 5. Heterochronic modelling experiment 2. The “ancestor” on the left has parameters W₀ =1.1, ΔW =0.05, D =0, S =2.3, T’₀ =2, ΔT’ =-0.03, and has 10 whorls. It has a form, including the slightly concave profile of the spire, which is similar to some members of the Family Volutidae. The next simulations are “descendants” derived from this by successive increments of acceleration (relative scales x 0.5, x 0.225, x 0.0875, respectively). All of these have parallels in the Volutidae, with the final form resembling the giant volutids in the genus Melo. The observation that the simulation predicts the large size of the final form supports the heterochronic hypothesis in the evolution of these gastropods.

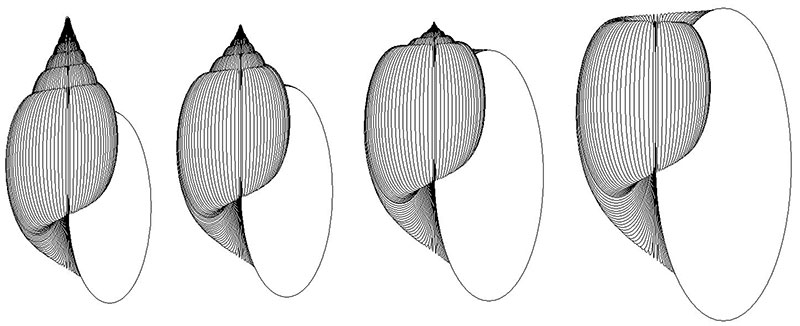
FIGURE 6. Heterochronic modelling experiment 3. The “ancestor” on the left has parameters W₀ =2, ΔW =-0.05, D =0, S =0.9, T’₀ =0.2, ΔT’ =0.07, and has eight whorls. As in Figure 4, this is a common general type of gastropod shell shape. The central simulation is a “descendant” derived from this by two increments of neoteny (relative scale x 0.5); the simulation on the right has resulted from two further increments of neoteny (relative scale x 0.39). All three simulations have analogues in the Family Helicidae of the Pulmonata, and this result constitutes a hypothesis for the possible heterochronic evolution of forms with flattened spires (depressed and sub-planispiral).

APPENDIX 1.

Use of the program HETEROSIM, and exercises for students.

The computer program HETEROSIM constructs geometrical shapes using the equations presented in this paper. The graphical construction is achieved by drawing opaque ellipses to represent successive positions of the whorl, with those nearest the viewer drawn last to create a rough impression of a solid 3D form. This graphical style is regarded as being satisfactory, but close inspection does reveal minor anomalies in the vicinity of the coiling axis. Other authors have produced renderings that are smoother and with a technically superior 3D appearance (e.g., Hammer and Bucher 2005; Noshita 2012), but this is thought to be unnecessary for current purposes, and in some respects the graphical style used here is clearer. HETEROSIM is restricted to simulations with elliptical whorl sections; this is thought to be appropriate, as attempting to find fits to other whorl shapes would be time-consuming and not relevant to the task of modelling heterochronic change in gross shell shape.

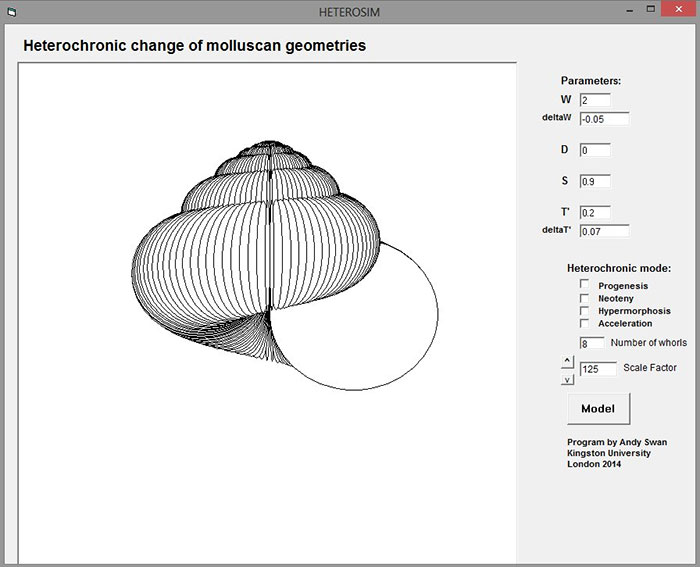
The user of the program is presented with eight boxes containing values that can be user-specified prior to heterochronic modelling: these are the six parameter values described in this paper, plus the number of whorls and a relative scale factor (see Appendix 2). The default values are those used in Figure 4. Clicking on the “MODEL” button then generates the simulation using the current parameters. (N.B. The parameters defined in this paper as W₀ and T’₀ appear on-screen as “W” and “T’”.)

The effect of heterochronic modes can then be simulated by clicking on the box(es) corresponding to the desired mode(s) (this will produce a “tick” in the box), and clicking on the “MODEL” button again. Repeated increments of the same or other modes can be executed. The modes can be de-selected by clicking on the ticked boxes. (For the sake of simplicity, and ease of use in a pedagogic environment, this version of the program offers only the default values for heterochronic change that are detailed in the main text of this paper.)

When the effect of heterochronic modes are modelled, the values of the parameters are updated. In one modelling experiment, it is expected that the user will not manually adjust the parameter values (except perhaps the scale factor) after setting-up the initial values.

The appropriate scale factor for the initial simulation is estimated by the program on the basis of the initial parameter values, but may nevertheless need to be adjusted. After applying heterochronic changes, the size of the simulated shell very often changes substantially. The scale factor can be adjusted readily by clicking on the “^” or “v” buttons. When this is done, all current heterochronic mode selections are switched off.

There is no special provision for capturing and printing graphics; the familiar <CTRL><ALT><PRNT SCRN> key combination can be used, or import facilities in graphics editing software.

The program should work on all PCs with Microsoft Windows or Windows emulation. It may be found that the program doesn’t initially run, and an error is shown that reports a missing Dynamic Link Library (.DLL) file. If so, this file can readily be found on the Microsoft web site and installed easily and free of charge. Users in European countries may need to change the decimal separator from a dot to a comma.

Exercises for Students

Initially, students should become familiar with the geometric parameters in the isometric case. Parameters Δ W and Δ T’ should both be set to zero, and W, T’, S and D adjusted (one at a time) so that the effect of each can be noted (this is good practice in gaining familiarity with any computer simulation). This can lead to more structured investigation:

1. Students should be introduced to the concept of morphospace, and a two-dimensional array of forms could be produced in the style of figure 2.2.3.1 in Swan (2001), perhaps with D and S kept constant and simulations with various permutations of W and T’ produced.

2. Students can then be given the task of finding parameter combinations that yield simulations similar to actual specimens. Illustrations of a range of specimens could be presented; these could include one or two allometric forms so that the key difference can be observed. Students should find that the adjustments required in order to more closely simulate isometric forms is quite intuitive. The failure to simulate allometric forms is instructive.

3. Students could be invited briefly to experiment with heterochronic changes on isometric forms. They will observe that there is no change in shape, even when there is change of size (in the case of progenesis and hypermorphosis).

Students can then be given the task of optimising all six parameter values for a given real allometric form. Members of the Pulmonata are good for this, especially the more typical members of the Helicidae. This optimisation is likely to be difficult, as this constitutes a search of six-dimensional morphospace, without an easy intuition of the direction in which the optimum lies. This is typical of the difficulty encountered when undertaking optimisation using models with large-dimensional parameter space in general.

4. Using a set of parameter values supplied by the instructor (perhaps the ones used in Figures 4, 5 and 6), students can experiment with the effect of the heterochronic modes. (In order to return to the starting point, they should note that an increment of neoteny can be reversed by an increment of acceleration and vice versa, and likewise for progenesis and hypermorphosis). They should attempt to understand how the “descendant” forms have resulted from the modification of the “ancestral” ontogeny.

5. For a more extended project, students could locate a source of illustrations of allometric gastropods from a specific taxonomic group (perhaps at Family level) and find the six optimal parameter values for one of the species (it is probably best to use one of the more conservative forms). A range of heterochronic “descendants” can then be produced for comparison with the variety of forms that actually occur. The plausibility of the heterochronic hypothesis for that group can then be critically assessed. (Note that, ideally, the phylogeny of the specimens in the chosen taxonomic group would be known, but this information is seldom available).

6. For more advanced study, students could be invited to consider the possible functional performance of the various forms and the ecology of the specified taxonomic group, and reach a verdict on whether heterochrony might be the means of producing a better-performing adult shape, or whether the “descendant” adult shape is merely a consequence of the favourability of evolutionary change in rates and timings in ontogenetic development.

APPENDIX 2.

“Screenshot” of the HETEROSIM program, as presented to the user.

Heterochrony in helicoid spiral cones: a computer model for demonstrating heterochronic evolution

Andrew Robert Henry Swan

Plain Language Abstract

The most commonly used computer models of mollusc shells use geometrical shapes that do not change shape as they grow. The model presented here has a simple modification that allows change of shape with growth. This in turn allows experimentation with heterochronic modes of evolution. Heterochronic evolution is where descendants differ from their ancestors in the rate of change of shape as they grow, and/or in the timing of cessation of growth. The results show that, by heterochronic changes, it is possible to produce a range of shell shapes that are similar to those that occur in groups of real molluscs, suggesting that these molluscs may have evolved in similar ways. The model can be used in teaching evolution at university level.

Resumen en Español

Heterocronía en conos espirales helicoidales: un modelo computacional para demostrar la evolución heterocrónica

Una modificación del modelo clásico de Raup del cono helicoidal basado en la espiral logarítmica permite la incorporación de parámetros para el cambio ontogenético en los principales valores de los parámetros geométricos. Las estructuras alométricas resultantes pueden ser modificadas por incrementos heterocrónicos simulados de manera que se pueden reproducir los efectos de la neotenia, aceleración, progénesis e hipermorfosis. Los experimentos realizados con el modelo, denominado HETEROSIM, producen conjuntos de formas que son consistentes con los que se dan dentro de las familias de la Clase Gastropoda, y, por lo tanto, la heterocronía es una hipótesis plausible para la evolución de estos taxones. Además de las aplicaciones en la investigación evolutiva, el modelo es una valiosa herramienta pedagógica en la enseñanza avanzada de la paleontología y la evolución.

Palabras clave: heterocronía; modelo computacional; morfoespacio; gasterópodos

Traducción: Enrique Peñalver

Résumé en Français

Hétérochronie chez les cônes de spirales hélicoïdales: un modèle informatique pour démontrer l'évolution hétérochronique

Une modification du modèle logarithmique hélicoïdale de spirale conique classique de Raup permet l'incorporation de paramètres pour le changement ontogénétique dans les principales valeurs des paramètres géométriques. Les structures allométriques qui en résultent peuvent être modifiées par incréments hétérochroniques simulées afin que les effets de la néoténie, l'accélération, la progenèse et l'hypermorphose puissent être produits. Les expériences avec le modèle, nommé HETEROSIM, produisent des suites de formes qui sont compatibles avec celles qui se produisent au sein des familles de la classe des gastéropodes, et donc l'hétérochronie est une hypothèse plausible pour l'évolution dans ces taxons. En plus des applications dans la recherche de l'évolution, le modèle est un outil pédagogique précieux dans l'enseignement de la paléontologie et de l'évolution avancée.

Mots-clés: Hétérochronie; modèle informatique; morpho-espace; gastéropodes

Translator: Kenny J. Travouillon

Deutsche Zusammenfassung

Heterochronie in helicoiden Spiralkegeln: ein Computermodell für die Darstellung heterochroner Evolution

Eine Modifizierung von Raup's klassischem helicoiden logarithmischen Spiralkegel-Modell erlaubt die Einbeziehung von Parametern für ontogenetische Veränderungen innerhalb der geometrischen Hauptparameter. Die resultierenden allometrischen Strukturen können mit simulierten heterochronischen Erhöhungen modifiziert werden, so dass die Effekte von Neotänie, Akzeleration, Progenesis und Hypermorphosis erzeugt werden können. Experimente mit dem Modell das HETEROSIM genannte wird, erzeugen Folgen von Formen die mit denen konsistent sind, die innerhalb der Familien der Klasse Gastropoda auftreten. Somit ist Heterochronie eine plausible Hypothese für die Evolution in diesen Taxa. Zusätzlich zu den Einsatzmöglichkeiten in der Evolutionsforschung ist das Modell ein wertvolles pädagogisches Werkzeug für das Unterrichten der erweiterten Paläontologie und Evolution.

Schlüsselwörter: Heterochronie; Computermodell; Morphospace; Gastropoden

Translator: Eva Gebauer

Arabic

Translator: Ashraf M.T. Elewa