Article Search
Volume 27.1
January–April 2024
Full table of contents
ISSN: 1094-8074, web version;
1935-3952, print version
Recent Research Articles
See all articles in 27.1 January-April 2024
See all articles in 26.3 September-December 2023
See all articles in 26.2 May-August 2023
See all articles in 26.1 January-April 2023
 Jordi Marcé-Nogué
Jordi Marcé-Nogué
Departament de Resistència de Materials i Estructures a l’Enginyeria
Universitat Politècnica de Catalunya
BarcelonaTech
Colom 11, 08222
Terrassa
Spain
jordi.marce@upc.edu
and Institut Català de Paleontologia Miquel Crusafont
Universitat Autònoma de Barcelona
Edifici ICP, Campus de la UAB s/n, 08193
Cerdanyola del Vallès
Spain
Jordi Marcé-Nogué (Igualada, 1979) has Bachelor degree of Industrial Engineering issued from Universitat Politècnica de Catalunya (Spain) in 2003 and PhD degree Resistència de Materials i Computational Biomechanics from Universitat Politècnica de Catalunya in 2009. He started as a research fellow in the Departament de Estructures a l'Enginyeria and from 2006 he has being a assistant teacher in Escola Tècnica Superior d'Enginyeria i Aeronàutica de Terrassa (UPC) and a researcher at Laboratory for the Innovation of Structures and Materials (LITEM).

 Adam Kłodowski
Adam Kłodowski
Department of Mechanical Engineering
Lappeenranta University of Technology
Skinnarilankatu 34, 53850
Lappeenranta
Finland
adam.klodowski@lut.fi
Adam Klodowski is currently post-doctoral researcher at Lappeenranta University of Technology, Finland. He works mostly in the field of dynamical simulations and modeling. His main work focus is in biomechanical simulations of the musculoskeletal systems of humans combining simulation and experimental methods together. In the recent time Adam Klodowski has developed interests towards musculoskeletal simulations of animals. In addition to his work in the field of biomechanics, he is also interested in classical technology field including 3D printing, machine dynamics and production engineering.

 Montserrat Sánchez
Montserrat Sánchez
Departament de Resistència de Materials i Estructures a l’Enginyeria
Universitat Politècnica de Catalunya
BarcelonaTech, Colom 11, 08222
Terrassa
Spain
Montserrat.sanchez@upc.edu
Dr. of Mechanical Engineer and professor at the Universitat Politècnica de Catalunya. She has participated in several national projects and agreements with companies. She is currently directing two doctoral theses, has participated in 12 competitive research projects (2 of them as principal investigator), has conducted 15 international publications and 12 conference contributions.

 Lluís Gil
Lluís Gil
Departament de Resistència de Materials i Estructures a l’Enginyeria
Universitat Politècnica de Catalunya
BarcelonaTech
Colom 11, 08222
Terrassa
Spain
lluis.gil@upc.edu
Lluís Gil (Barcelona, 1966) achieved a civil engineering degree in 1992 and a PhD from Universitat Politecnica de Catalunya UPC in 1997. He currently is associate professor at UPC in the field of aerospace structures. Director of research Laboratory for the Innovation of Structures and Materials (LITEM). Lecturer of continuum mechanics and engineering structures. Interested in NDT, composites and new materials. ORCID:0000-0002-2007-4846.
FIGURE 1. Simplification of the center of head movement as a joint in extinct Temnospondyli amphibian when biting. Elaborated from the original image (en.wikipedia.org/wiki/File:Jammerbergia_formops.jpg). Under license: CC BY-SA 3.0 (creativecommons.org/licenses/by-sa/3.0/).
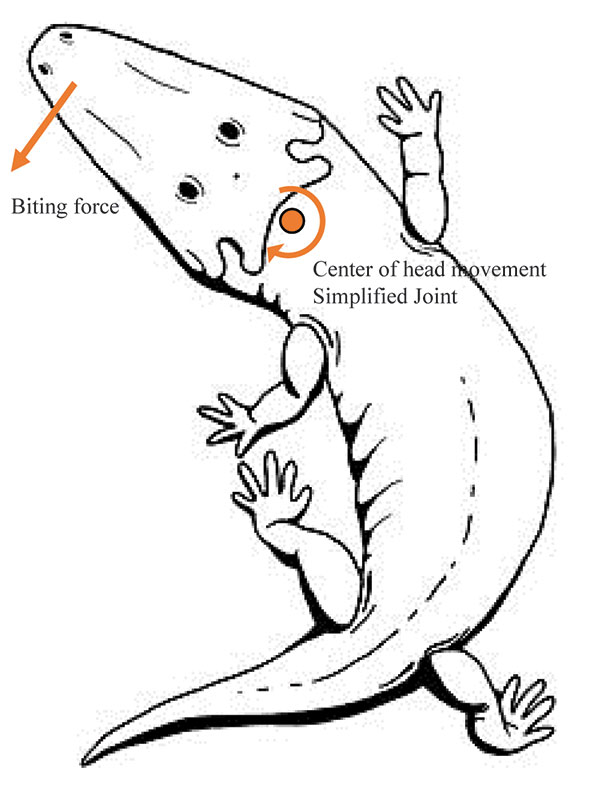
FIGURE 2. Studied test cases of different feeding movements when applying a force F=800 N in the direction of the red arrow (when the force is perpendicular at the view the red arrow is a red dot). Case 1A, 2A and 3A with a fixed boundary condition in the condyle without the web of beams. Case 1B, 2B and 3B with the web of beams in the condyle and a fixed boundary condition.
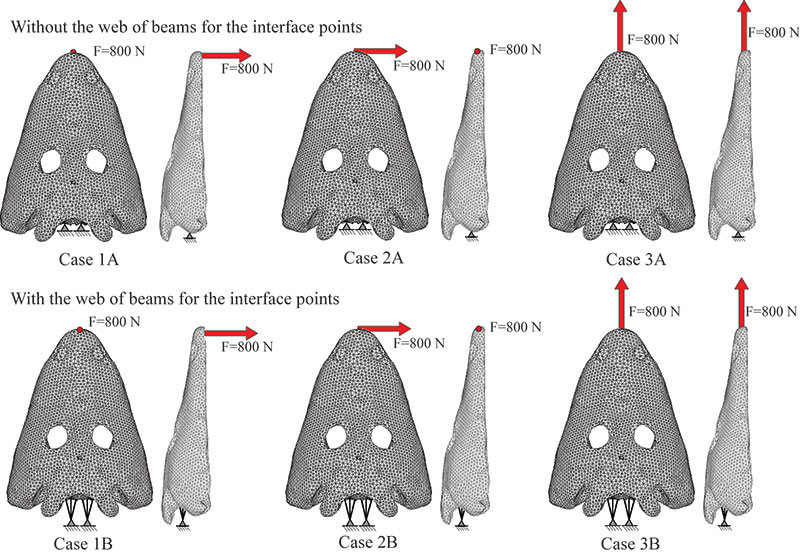
FIGURE 3. Locations of the nine nodes at which the stresses were evaluated.
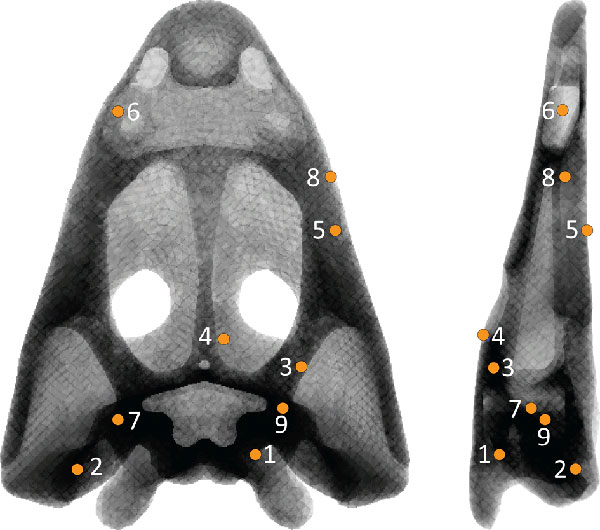
FIGURE 4. Von Mises stress distribution in the skull for the Static Analysis in FEA in cases 1A, 2A, 3A, 1B, 2B and 3B.
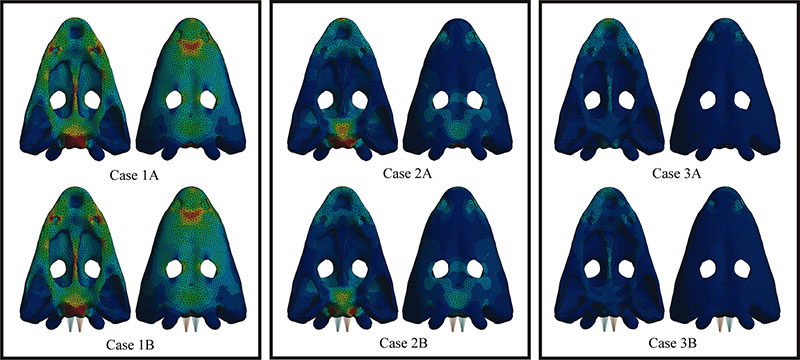
FIGURE 5. First 12 modes of the skull in case 1 (without web of beams in the model).
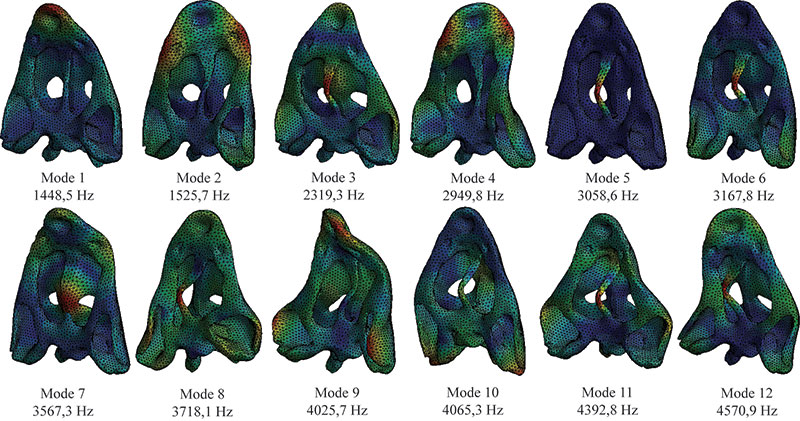
FIGURE 6. First 12 modes of the skull in case 2 (with the web of beams in the model).
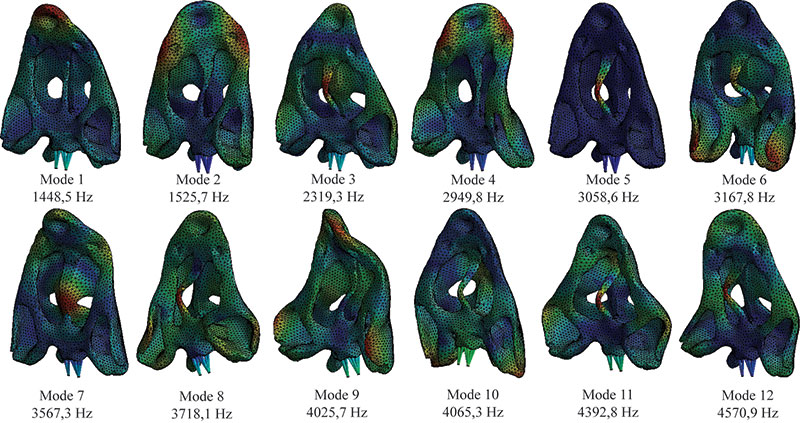
FIGURE 7. Average error with respect to the number of deformation modes used.
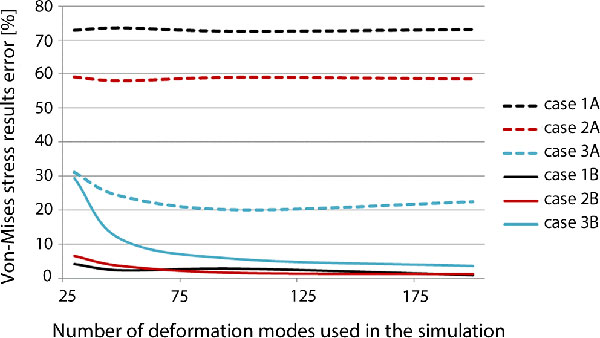
TABLE 1. Equivalent Von-Mises stress results errors at selected nodes - test cases 1A, 2A and 3A.
TABLE 2. Equivalent Von-Mises stress results errors at selected nodes - test cases 1B, 2B and 3B.
All supplemental tables are presented in one ZIP file for download.
TABLE S1. Stress results obtained from the FEA, FMSD and the error of FMSD with respect to the FEA for test case A.
TABLE S2. Stress results obtained from the FEA, FMSD and the error of FMSD with respect to the FEA for test case B.
TABLE S3. Two-hundred Modes obtained for case 1 without the web of beams and its associated frequency.
TABLE S4. Two-hundred Modes obtained for case 2 with the web of beams and its associated frequency.
Coupling finite element analysis and multibody system dynamics for biological research
Plain Language Abstract
Flexible Multibody System Dynamics (FMSD) is a simulation technique that can be used to study the behavior of the mechanical systems that consists of one or more deformable bodies. FMSD is based in the total coupling of Finite Element Analysis (FEA) and Multibody System Dynamics (MSD) to explore the feeding mechanism in a skull of Edingerella madagascariensis. The applicability of it in the feeding mechanism of vertebrate structures is tested because, since today, biological research in this field is currently dominated by both pure finite element studies and studies based on rigid body multibody method without the total coupling of both methodologies.
Resumen en Español
Uniendo el análisis de elementos finitos y la dinámica de sistemas multicuerpo para la investigación en biología
La Dinámica de Sistemas Multicuerpo Flexible (DSMF) es una técnica de simulación que puede ser usada para estudiar el comportamiento de sistemas mecánicos que consisten en uno o más cuerpos deformables. Un cuerpo deformable puede ser modelado usando un número de enfoques mientras que la formulación del marco de referencia flotante es un enfoque ampliamente utilizado. Con ese enfoque, la flexibilidad dentro de la Dinámica de Sistemas Multicuerpo (DSM) se describe implementando el Análisis de Elementos Finitos (AEF) con un enfoque de reducción modal. La aplicabilidad de la DSMF en el mecánico alimentario de estructuras de vertebrados es evaluado con el fin de utilizar el potencial del método en investigaciones biológicas. La Dinámica de Sistemas Multicuerpo Flexible es explorada estudiando el mecanismo de alimentación de un cráneo de Edingerella madagascariensis. En primera instancia se realiza un análisis estructural estático usando AEF. Luego, se obtienen soluciones dinámicas basadas en DSMF variando el número de modos de deformación usados en el análisis de reducción modal. La conclusión es que el uso de este enfoque es viable y eficiente para el estudio de mecanismos de alimentación en estructuras de vertebrados cuando se pretende evaluar una respuesta dinámica.
Palabras clave: AEF; FEA; DSM; flexibilidad; mecánica computacional; paleontología; vertebrados
Traducción: Diana Elizabeth Fernández
Résumé en Français
Combiner l'analyse par les éléments finis avec la dynamique des systèmes multicorps pour la recherche en biologie
La Dynamique des Systèmes Multicorps Flexibles (DSMF) est une technique de simulation qui peut être utilisée pour étudier le comportement des systèmes mécaniques composés d'au moins un corps déformable. Un corps déformable peut être modélisé par un certain nombre d'approches, celle du cadre flottant de la formulation de référence étant largement utilisée. Dans cette approche, la flexibilité dans la Dynamique des Systèmes Multicorps (DSM) est décrite en employant l'Analyse par les Éléments Finis (AEF) avec une réduction modale. L'applicabilité de la DSMF aux mécanismes de prise de nourriture des vertébrés est testée dans l'optique d'exploiter le potentiel de cette méthode pour la recherche en biologie. La Dynamique des Systèmes Multicorps Flexibles est explorée en étudiant le mécanisme de prise de nourriture à partir d'un crâne d'Edingerella madagascariensis. Dans un premier temps, une analyse structurelle statique est effectuée en utilisant l'AEF, et dans un second temps, les solutions dynamiques basées sur la DSMF sont obtenues en faisant varier le nombre de modes de déformation utilisés dans l'analyse de réduction modale. En conclusion, l'utilisation de cette approche est réalisable et efficace pour l'étude des mécanismes de prise de nourriture des vertébrés quand une réponse dynamique doit être évaluée.
Mots-clés : AEF ; DSM ; flexibilité ; mécanique statistique ; paléontologie ; vertébrés
Translator: Antoine Souron
Deutsche Zusammenfassung
Verbindung von Finite-Elemente-Analyse und Mehrkörper-Systemdynamik in der biologischen Forschung
Flexible Mehrkörper-Systemdynamik (FMSD) ist eine Simulationstechnik die zum Untersuchen des Verhaltens von mechanischen Systemen genutzt werden kann, die aus einem oder mehreren verformbaren Körpern bestehen. Ein verformbarer Körper kann mit einer Reihe von Ansätzen modelliert werden, während der Floating Frame der Referenzformulierung ein häufig verwendeter Ansatz ist. Bei diesem Ansatz wird Flexibilität innerhalb der Mehrkörper-Systemdynamik (MSD) beschrieben indem die Finite-Elemente-Analyse (FEA) mit einem modalen Reduzierungsansatz verwendet wird. Es wird die Anwendbarkeit einer FMSD bei Ernährungsmechanismen von Wirbeltieren getestet, um das Potential der Methode in der biologischen Forschung anzuwenden. Flexible Mehrkörper-Systemdynamik wird am Beispiel des Ernährungsmechanismus von Edingerella madagascariensis untersucht. Zuerst wird eine statische Strukturanalyse mit FEA durchgeführt und im zweiten Schritt werden dynamische Lösungen basierend auf FMSD erzielt, indem die Anzahl der Verformungsarten in der modalen Reduktionsanalyse variiert wird. Die Schlussfolgerung ergibt, dass die Verwendung dieses Ansatzes praktikabel und effizient zum Untersuchen von Ernährungsmechanismen bei Wirbeltieren ist, wenn ein Dynamikverhalten evaluiert werden soll.
Schlüsselwörter: FEA; MSD; Flexibliät; rechnergestützte Mechanik; Paläontologie; Vertebraten
Translator: Eva Gebauer
Arabic

Translator: Ashraf M.T. Elewa
-
-
-
Review: The Princeton Field Guide to Mesozoic Sea Reptiles
 The Princeton Field Guide to Mesozoic Sea Reptiles
The Princeton Field Guide to Mesozoic Sea ReptilesArticle number: 26.1.1R
April 2023


 Poster Winners 2024
Poster Winners 2024