Virtual whitening of fossils

Virtual whitening of fossils using polynomial texture mapping

Øyvind Hammer and Jelena Spocova

Article number: 16.2.4T
https://doi.org/10.26879/384
Copyright Palaeontological Association, August 2013

Author biographies
Plain-language and multi-lingual abstracts
PDF version

Submission: 13 March 2013. Acceptance: 23 June 2013

{flike id=465}

ABSTRACT

Polynomial Texture Mapping (PTM) is an established technique of digital photography, allowing virtual relighting and modification of surface reflective properties in order to bring out subtle detail. We describe a new, simple method for transforming PTM files that mimics whitening, a traditional procedure for fossil photography. The method is based on the estimation of surface normal vectors from the PTM coefficients. These vectors are used to construct a diffuse, isotropic (Lambertian) lighting model that is only dependent on local surface slope. It is also possible to simulate the effect of whitening agent not penetrating into depressions, increasing the topography-dependent contrast.

Øyvind Hammer. Natural History Museum, University of Oslo, Pb. 1172 Blindern, 0318 Oslo, Norway. oyvind.hammer@nhm.uio.no
Jelena Spocova. Norwegian Broadcasting Corporation, Pb. 8500 Majorstuen, 0340 Oslo, Norway. jelena.spocova@gmail.com

Keywords: image enhancement; digital imaging; illustration; PTM

Final citation: Hammer, Øyvind and Spocova, Jelena. 2013. Virtual whitening of fossils using polynomial texture mapping, Palaeontologia Electronica Vol. 16, Issue 2; 4T; 10p.  https://doi.org/10.26879/384
palaeo-electronica.org/content/2013/465-virtual-whitening-of-fossils

Whitening

A traditional visual-light photograph depicts variation in brightness and colour caused by two different surface properties. The varying orientation of the imaged surface with respect to the light source produces shading, which is the primary cue for our perception of three-dimensional shape in a two-dimensional image. In addition, most surfaces also vary spatially in their inherent colour and albedo. While this latter variation may contain useful information for many objects, it is merely a nuisance for most fossils, where the colour variation is mostly due to secondary diagenetic processes. Removing the variation in colour can therefore give dramatic improvement in image quality. Unfortunately, once a traditional photograph of an object has been taken, the colour and shading information are mixed and confounded, and can not be separated.

One approach for separating colour from shading is to obtain a three-dimensional representation of the surface, and then produce a shaded image using a synthetic lighting model. The three-dimensional digitization could involve photogrammetry (e.g., Falkingham, 2012), laser scanning or CT scanning (e.g., Görög et al., 2012). Although feasible, such procedures can be time consuming and expensive. More importantly, they do not easily provide spatial resolution comparable with the multi-megapixel capabilities of modern digital cameras. For example, Falkingham (2012) produced photogrammetric point clouds of between 180,000 and 2 million points, with computation times from 0.5 to 12 hours on an eight-processor computer. Laser scanning typically has a resolution of 0.1 mm (cf. Falkingham, 2012). Microfocus X-ray tomography can provide much higher resolution, but at relatively high cost and long acquisition and computation time. In comparison, the PTM technique used here gives full camera resolution (e.g., 8 megapixels) with a total acquisition and computation time of less than five minutes on a standard office computer.

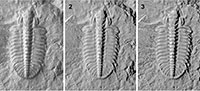
Traditionally, colour has been physically removed from fossil specimens by coating with ammonium chloride. Such whitening is now standard procedure for professional illustration of fossils (Teichert, 1947; Marsh and Marsh, 1975; Feldmann, 1989; Green, 2001). Optionally, the specimen can be painted black prior to whitening. If the ammonium chloride is applied sparingly, the black paint will shine through in depressions and on the lee side of the application direction, enhancing the three-dimensional contrast. Whitening can produce spectacular results and is generally recommended (Figure 1). However, it requires a gas burner, some glassware, the whitening agent itself, a dry atmosphere, and a certain degree of operator skill. These are not always conveniently available. Whitening is also impractical for very large specimens. The whitening and the subsequent removal of ammonium chloride and paint, often in water, may cause a risk to fragile fossils. Finally, the use of a burner has its own perils – whitening has triggered fire alarms in our museum on several occasions!

Polynomial Texture Mapping

The Polynomial Texture Mapping (PTM) technique was introduced by Malzbender et al. (2000, 2001). A number of pictures (typically 50) are taken with a consumer-grade digital camera in a fixed position, and also with the imaged object held stationary. For each picture, a single point light source is placed in a unique, predetermined position. The procedure can be carried out conveniently with a purpose-built collection of 50 flash bulbs or LEDs under computer control, but it is also possible to use a single light source that is moved manually or robotically. In either case, the data acquisition is fast and cheap.

For data reduction, the colour and/or luminosity of each pixel, as functions of incoming light direction, are fitted to biquadratic polynomials. The resulting coefficients for all pixels are archived in a PTM file. Interactive software then allows virtual relighting (positioning of one or several virtual light sources) and certain transformations of the reflective properties that can dramatically increase the visibility of subtle features.

PTM is gaining popularity for imaging fossils (Hammer et al., 2002) and archaeological artefacts (Malzbender et al., 2000; Mudge et al., 2005; Earl et al., 2010). In addition to the scientific value of enhancing minute variation in surface topography, the technique can be used for virtual interactive museum exhibits for the general public on the web.

The PTM representation provides exactly the separation of colour from shading that is required for a computerized whitening procedure. A partial whitening effect can be obtained from existing PTM rendering software by manipulating the parameters of the "specular enhancement" effect (Malzbender et al., 2001). Specifically, the Kd (diffuse) parameter is set to zero. However, this method results in a Phong rather than Lambertian reflectance, which tends to produce a shiny, metallic effect that may not be desirable (Figure 2). Below, we describe a simple transformation of PTM coefficients that provides complete, matte whitening, and an additional 'black paint' effect to enhance contrast based on local curvature.

METHODS

PTM Acquisition

PTMs were acquired using a computer-controlled flash setup in the Natural History Museum in Oslo. The equipment was described by Malzbender et al. (2001) and Hammer et al. (2002). Pictures were taken with an SLR camera (Canon EOS 1000D) with a macro lens.

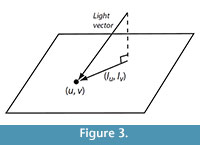
We use the LRGB format for representing the PTM (Malzbender et al., 2001). For each pixel, colour normalized to a constant luminosity is stored as conventional RGB (red-green-blue). In addition, for each pixel, luminosity L, varying over the direction of incoming light, is encoded using a biquadratic polynomial with six coefficients a₀ - a₅. With (u, v) the pixel coordinates and (l_u, l_v) the projection of the normalized light vector onto the image plane (Figure 3), we have

The luminosity polynomial for each pixel is fitted to the acquired image stack data using a least-squares method. The procedure gives a total of nine values for each pixel, namely R, G, B, and a₀ - a₅. These values are stored in an efficient binary file format (Malzbender et al., 2001).

In practical terms, the whole acquisition chain, from computer-controlled photography up to and including the polynomial fitting, is fully automated. The only required user intervention is to place the specimen under the flash dome, focus the camera, and click a button. The PTM file is then produced in a couple of minutes, depending on image resolution. However, although the necessary software modules are freely available (e.g., Malzbender 2001), we are not aware of any commercial, complete, 'turn-key' PTM system. Some hardware and software integration is therefore required to construct a practical setup.

Virtual Whitening

Malzbender et al. (2001) described the estimation of the surface normal vector at each pixel from the PTM biquadratic luminosity coefficients, by the analytical maximization of the luminance function. In effect, the normal vector is assumed to point in the opposite direction of the direction of incoming light that gives the strongest reflection. The resulting normal vector is

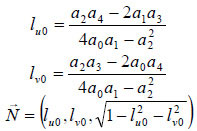
Some further processing may be necessary to make the normal vector estimation more robust. The PTM method is quite unique in allowing the calculation of normal vectors without any information about surface height, and without any spatial derivatives. Normal vectors can therefore be extracted reliably even if (in fact, especially if) the surface has a relief of only a few microns, a useful property for flattened fossils (Hammer et al., 2002).

The next step in the whitening procedure is to define a surface reflectance model. To simulate the matte surface produced by ammonium chloride whitening, a purely diffuse and isotropic (Lambertian) reflection model is appropriate. Specular reflection can be added later if desired, using the specular enhancement function available in PTM rendering software. Lambertian reflection can be computed simply as the inner product between the normalized light direction vector and the surface normal vector . In addition we include an ambient light term k_a. The reflected light luminosity is then

The RGB values are set to white, i.e., (1, 1, 1). This reflection model could be implemented directly by the PTM renderer. Alternatively, it is possible to whiten by stand-alone pre-processing of the PTM file. This approach was used here in order to avoid modification of available PTM rendering software, but also to allow distribution of already whitened PTM files. In this case, it is necessary to reformulate the Lambertian reflection model in terms of the luminosity biquadratic polynomial stored in the PTM file. The constant and first-order terms in (l_u, l_v) in the reflection model are directly translatable into terms in the PTM polynomial, but not the final square root term. A bivariate Taylor expansion around the origin gives

.

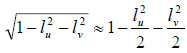To ensure zero luminosity for grazing light, we instead use simply

.

Collecting terms gives the final whitened PTM biquadratic luminosity model

.

Black Paint Effect

In the traditional whitening method, the surface is sometimes painted black prior to whitening. This procedure causes darkening of depressions where the ammonium chloride does not cover fully, increasing the three-dimensional contrast. Such an effect can be partly emulated in the PTM context because the estimated normal vectors give direct three-dimensional information. The topographic data can be used to reduce the RGB values for a darkening effect.

Although the surface elevation f is not known a priori, its gradient can be calculated from the normal vectors:

.

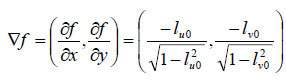Note again that this estimate does not require spatial differences, and therefore maintains the full camera resolution. The gradient can be integrated to produce an estimated elevation model (Hammer et al., 2002), but this is not required for the present purpose. Instead, we differentiate the gradient to produce a simple scalar measure of local curvature as given by the Laplacian

.

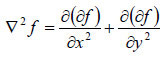The Laplacian is estimated by first-order differences on , i.e. for discrete pixel coordinates (i, j) and pixel size h we use

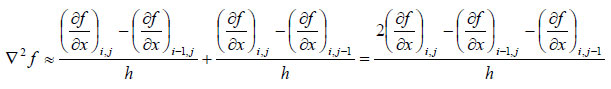
The RGB values are reduced linearly as a function of the Laplacian, considering that positive curvature represents a concave surface.

The high-pass spatial frequency response of the Laplacian gives highest sensitivity to smallest features, which may produce undesired noise. The Laplacian may therefore be smoothed by a simple blur operator, giving an overall bandpass response that can be tuned to the scale of interest.

A simple command.line program was written in C to read a PTM file, estimate the normal vectors and curvatures, and make a new whitened PTM file.

RESULTS AND DISCUSSION

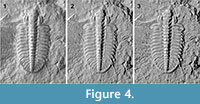
Examples of the virtual whitening procedure are shown in Figure 4,Figure 5,Figure 6, and Figure 7. The results are encouraging, and the method seems capable of competing with traditional whitening. Achieving such high resolution, limited only by the camera, would be expensive and time-consuming with photogrammetry or CT scanning, and impossible with a standard laser.

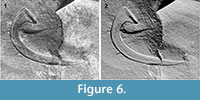Not shown are the poorer results from objects with much higher relief, such as very convex brachiopods. For such objects, self-shadowing during the PTM image acquisition leads to inaccuracies in the normal vector estimation. The whitening procedure seems very sensitive to these inaccuracies, possibly because the variation in RGB values, which otherwise partly mask the artefacts from inaccurate luminosity, are discarded. As implemented here, the whitening method seems best suited to objects with small topographic relief. However, as shown by Drew et al. (2009), robust regression methods may be used to detect shadows and specular highlights, with the potential to greatly improve normal vector estimation in the presence of self-shadowing. This approach may be included in our virtual whitening procedure in the future.

ACKNOWLEDGEMENTS

Thanks are due to two anonymous reviewers for useful comments on the initial manuscript. The trilobite specimen in Figure 4 was collected by N.J. Butterfield and J. Ortega-Hernandez. Thanks to K. Hryniewicz for assistance with the physical whitening and to our technical staff for temporarily disabling the fire alarm.

REFERENCES

Drew, M., Hajari, N., Hel-Or, Y, and Malzbender, T. 2009. Specularity and shadow interpolation via robust polynomial texture maps. Proceedings of the British Machine Vision Conference, 2009.

Earl, G., Martinez, K., and Malzbender, T. 2010. Archaeological applications of polynomial texture mapping: analysis, conservation and representation. Journal of Archaeological Science, 37:2040-2050.

Falkingham, P.L. 2012. Acquisition of high resolution three-dimensional models using free, open-source, photogrammetric software. Palaeontologia Electronica, 15(1):15pp
palaeo-electronica.org/content/issue-1-2012-technical-articles/92-3d-photogrammetry.

Feldmann, R.M. 1989. Whitening fossils for photographic purposes, p. 342-346. In Feldmann, R.M., Chapman, R.E., and Hannibal, J.T. (eds.), Paleotechniques. The Paleontological Society Special Publication, 4:342-346.

Görög, Á., Szinger, B., Tóth, E., and Viszkok, J. 2012. Methodology of the micro-computer tomography on foraminifera. Palaeontologia Electronica, 15(1):15 pp;
palaeo-electronica.org/content/issue-1-2012-technical-articles/121-methodology-of-ct-on-forams.

Green, O.R. 2001. A Manual of Practical Laboratory and Field Techniques in Palaeobiology. Kluwer Academic Publishers, Dordrecht, The Netherlands.

Hammer, Ø., Bengtson, S., Malzbender, T., and Gelb, D. 2002. Imaging fossils using reflectance transformation and interactive manipulation of virtual light sources. Palaeontologia Electronica, 5(4):9 pp, 639KB;
palaeo-electronica.org/2002_1/fossils/issue1_02.htm.

Malzbender, T., Gelb, D., and Wolters, H. 2001. Polynomial texture maps. Proceedings of ACM Siggraph, 2001:519-528.

Malzbender, T., Gelb, D., Wolters, H., and Zuckerman, B. 2000. Enhancement of shape perception by surface reflectance transformation. Hewlett-Packard Technical Report HPL-2000-38, March 2000.

Marsh, L.F. and Marsh, R.C. 1975. New techniques for coating paleontological specimens prior to photography. Journal of Paleontology, 49:565-566.

Mudge, M., Voutaz, J.P., Schroer, C., and Lum, M. 2005. Reflection transformation imaging and virtual representations of coins from the hospice of the grand St. Bernard, p. 29-39. In Mudge, M., Ryan, N., and Scopigno, R. (eds.), Proceedings of 6th International Symposium on Virtual Reality, Archaeology and Cultural Heritage (VAST2005). Eurographics Association.

Teichert, C. 1947. A simple device for coating fossils with ammonium chloride. Journal of Paleontology, 22:102-104.