RESULTS
Diversity
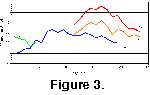 Diversity results for the three different data sources are shown in
Figure 3 and summarized in
Table 4. For Abelmann's data, two different curves are shown: a raw data curve (with higher diversity values) and a second, 'corrected' curve. This latter curve shows only data for taxa whose upper or lower ranges are not artificially truncated within the composite range chart by the lack of primary observational information in one or more sites. This correction was judged to be necessary as the observed diversity changes would otherwise be partially controlled by the arbitrary cutoff of ranges at the upper or lower boundaries of individual site sample sets used in Abelmann's study. This, of course, eliminates significant numbers of taxa from the author's data sets, but at least provides a method for recording and analyzing data that is consistent between different authors' data sets.
Diversity results for the three different data sources are shown in
Figure 3 and summarized in
Table 4. For Abelmann's data, two different curves are shown: a raw data curve (with higher diversity values) and a second, 'corrected' curve. This latter curve shows only data for taxa whose upper or lower ranges are not artificially truncated within the composite range chart by the lack of primary observational information in one or more sites. This correction was judged to be necessary as the observed diversity changes would otherwise be partially controlled by the arbitrary cutoff of ranges at the upper or lower boundaries of individual site sample sets used in Abelmann's study. This, of course, eliminates significant numbers of taxa from the author's data sets, but at least provides a method for recording and analyzing data that is consistent between different authors' data sets.
In all three authors' data sets, reported diversity declines near the beginning and end of their study intervals. Diversity, in both versions of Abelmann's curve and in Lazarus' data, increases gradually in the early Miocene and falls significantly near the early - middle Miocene boundary (ca., 15 Ma), although some of the drop in diversity at this time is due to the differences in overall diversity reported between the two authors. Diversity within Lazarus' data set rises from the middle Miocene into the late Miocene and falls significantly into the early Pliocene. Low diversity is also recorded in the early Pliocene by Caulet. Diversity recovers in the late Pliocene and Pleistocene within Caulet's data set but does not reach the levels seen by either Lazarus or Abelmann in earlier Miocene intervals. .
FOs, LOs and Total Turnover
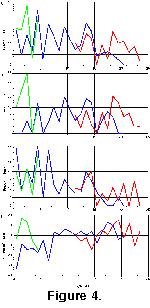 First occurrences (FOs), last occurrences (LOs) and total turnover (the sum of FOs and LOs) per 1 m.y. interval are shown for all three data sets in
Figure 4A-C and are summarized in
Table 4. Total turnover, which summarizes the relative intensity of faunal change, is given in
Figure 4A. The overall pattern shows a trend from lower rates of change (ca. 20% turnover per m.y.) in the early Miocene to very high rates of change (as much as 50% turnover per m.y.) in the Plio-Pleistocene. The trend is far from monotonic, however, with major changes at a ca. 2-3 m.y. scale in the mid to early late Miocene, and at ca. 1 m.y. scales in the latest Miocene to Recent. As 1 m.y. is the sampling scale , the true scale of variability in the latter interval may even be shorter.
First occurrences (FOs), last occurrences (LOs) and total turnover (the sum of FOs and LOs) per 1 m.y. interval are shown for all three data sets in
Figure 4A-C and are summarized in
Table 4. Total turnover, which summarizes the relative intensity of faunal change, is given in
Figure 4A. The overall pattern shows a trend from lower rates of change (ca. 20% turnover per m.y.) in the early Miocene to very high rates of change (as much as 50% turnover per m.y.) in the Plio-Pleistocene. The trend is far from monotonic, however, with major changes at a ca. 2-3 m.y. scale in the mid to early late Miocene, and at ca. 1 m.y. scales in the latest Miocene to Recent. As 1 m.y. is the sampling scale , the true scale of variability in the latter interval may even be shorter.
First and last occurrence data (Figure 4B-C)) reveal that two contrasting patterns contribute to the overall pattern of turnover. First occurrences vary substantially on short time scales, but over the entire interval studied show no discernible trend, although there are two broad intervals of low FO rates in the late middle Miocene and latest Miocene. Last occurrence rates, by contrast, are more clearly non-uniform, being low in the early Miocene, higher in the mid-Miocene to Recent, and with distinct peaks in between 15-13 Ma and near the Miocene-Pliocene boundary. These two differing faunal change characteristics are compared in
Figure 4D, which is the percent net change of the faunal data. This statistic, being a difference value and thus inherently more noisy than other measurements, nonetheless shows broadly positive net rates of change for the early Miocene and late Pliocene-Recent, with substantial net negative rates of change between 15-13 Ma and the near Miocene-Pliocene boundary.
Longevity Distributions
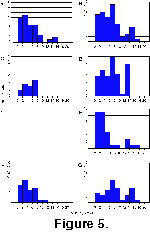 Given that the time intervals studied by the authors are similar to the average taxon longevity, truncation of ranges—and thus truncated longevities—are a major problem. Analyzing only non-truncated taxa is not in itself an adequate solution to this problem, as it preferentially excludes long ranging taxa. Including truncated ranges avoids this problem, although of course it adds artificially shortened ranges as well. Thus, the analysis was done for both truncated and non-truncated taxon ranges. The distribution of taxon longevities is given in
Figure 5A-G and
Table 1,
Table 2, and
Table 3, beginning with data from Lazarus (1992), the data set least affected by truncation problems. Non-truncated taxon longevities in this data set (Fig. 5A) show a noticeably non-Gaussian distribution, with both skew towards short longevities (mode at 2-4 m.y.) and a suggestion of bimodality with a gap at 10-12 m.y. This latter gap, however, is based on too few data to be convincing in itself. When truncated taxon ranges are included (Fig. 5B), the general pattern largely remains. The distribution is still non-Gaussian, with a clearly bimodal distribution of long ranging taxa (mode 14-16 m.y.), short ranging taxa (the mode at 6-8 m.y. now shifted towards larger values), and a distribution minimum at 10-12 m.y..
Given that the time intervals studied by the authors are similar to the average taxon longevity, truncation of ranges—and thus truncated longevities—are a major problem. Analyzing only non-truncated taxa is not in itself an adequate solution to this problem, as it preferentially excludes long ranging taxa. Including truncated ranges avoids this problem, although of course it adds artificially shortened ranges as well. Thus, the analysis was done for both truncated and non-truncated taxon ranges. The distribution of taxon longevities is given in
Figure 5A-G and
Table 1,
Table 2, and
Table 3, beginning with data from Lazarus (1992), the data set least affected by truncation problems. Non-truncated taxon longevities in this data set (Fig. 5A) show a noticeably non-Gaussian distribution, with both skew towards short longevities (mode at 2-4 m.y.) and a suggestion of bimodality with a gap at 10-12 m.y. This latter gap, however, is based on too few data to be convincing in itself. When truncated taxon ranges are included (Fig. 5B), the general pattern largely remains. The distribution is still non-Gaussian, with a clearly bimodal distribution of long ranging taxa (mode 14-16 m.y.), short ranging taxa (the mode at 6-8 m.y. now shifted towards larger values), and a distribution minimum at 10-12 m.y..
The data of Abelmann (1992a), covering only the older Miocene, also shows these patterns, although the numerous truncations in her data set, due to the lack of specific taxon data from some of her study sites, makes the analysis less robust. For her non-truncated ranges, the distribution of longevities (Fig. 5C) is similar to that for Lazarus with truncated ranges included, although the total number of taxa is very limited, and no longer ranging species were observed. When truncated range data are included (Fig. 5D) the longevity distribution matches that of Lazarus, although, due to the limited total time of her study interval, long-ranging species in the second distributional mode (>10-12 m.y.) are all recorded in a single—and thus artificially high-valued—bin at 12-14 m.y.
Too few non-truncated species ranges were available in
Caulet's (1991) data set to make a distributional analysis of non-truncated taxa ranges worthwhile. Given the very short time interval studied and the apparent presence of significant numbers of much longer-ranging species, Caulet's data on truncated species ranges was supplemented by locating in Lazarus' data the FO for as many of his taxa as possible that range below the base of his study interval. Given the taxonomic differences between the authors, this approach (as noted in the introduction) is risky, and only a few taxa could be matched with some degree of confidence in the uniformity of taxonomic concept. The result is shown in
Figure 5E, which very closely resembles that of
Lazarus' (1992) for untruncated ranges.
Lastly, longevity distributions were summarized for taxa originating in two different time intervals within Lazarus' data (including truncated range taxa): prior to, and after, 13 Ma.
Figure 5F shows the data for species originating prior to 13 Ma. Here the distribution is very bimodal, and, barring the absence of an upper value limit effect, is very similar to the pattern seen in Abelmann's data. The longevity distribution for species originating after 13 Ma is given in
Figure 5G. Here there is no indication of bimodality, and the distribution is skewed towards short-ranging taxa (mode at 2-4 m.y.)
Taxonomic Group Effects
Radiolarians are a diverse group of organisms with a wide range of ecologic preferences and preferred habitats, which is presumed to be reflected in their taxonomic structure. Basic data on the longevity of taxa are given for different time intervals in
Table 5, where the longevities (drawn from the Lazarus data set) are presented not only for radiolarians as a whole, but also for each of the two major taxonomic subgroups within them—the Nassellaria and Spumellaria. Although at first glance there seems to be no major difference between these two groups (average longevity for both Nassellaria and Spumellaria over the entire Neogene interval studied is 4.8 m.y. for those taxa whose ranges are not truncated), more detailed comparisons reveal substantial differences in the longevity characteristics for the two groups. Spumellarians tend to be longer lived than nassellarians in the older part of the study interval (mean longevities of 7.28 vs. 5.95 m.y., untruncated ranges only), and are relatively more important as a fraction of the total diversity (42% of the taxa in >13 Ma sediments, vs. only 31% in <13 Ma sediments). There is also a clear difference between older and younger intervals which affects both nassellarians and spumellarians - younger taxa in both groups are shorter ranging than they are in the same taxonomic group in older intervals (3.79 vs. 5.95 for Nassellaria, 3.42 vs. 7.28 for Spumellaria). In fact, in <13 Ma sediments the average longevity of the two groups is very similar, or possibly even reversed, with nassellarians being (albeit only slightly) more long lived than spumellarians (3.79 vs. 3.42 m.y.).
 Diversity results for the three different data sources are shown in
Figure 3 and summarized in
Table 4. For Abelmann's data, two different curves are shown: a raw data curve (with higher diversity values) and a second, 'corrected' curve. This latter curve shows only data for taxa whose upper or lower ranges are not artificially truncated within the composite range chart by the lack of primary observational information in one or more sites. This correction was judged to be necessary as the observed diversity changes would otherwise be partially controlled by the arbitrary cutoff of ranges at the upper or lower boundaries of individual site sample sets used in Abelmann's study. This, of course, eliminates significant numbers of taxa from the author's data sets, but at least provides a method for recording and analyzing data that is consistent between different authors' data sets.
Diversity results for the three different data sources are shown in
Figure 3 and summarized in
Table 4. For Abelmann's data, two different curves are shown: a raw data curve (with higher diversity values) and a second, 'corrected' curve. This latter curve shows only data for taxa whose upper or lower ranges are not artificially truncated within the composite range chart by the lack of primary observational information in one or more sites. This correction was judged to be necessary as the observed diversity changes would otherwise be partially controlled by the arbitrary cutoff of ranges at the upper or lower boundaries of individual site sample sets used in Abelmann's study. This, of course, eliminates significant numbers of taxa from the author's data sets, but at least provides a method for recording and analyzing data that is consistent between different authors' data sets.

