| |
TREE SEARCH ALGORITHM
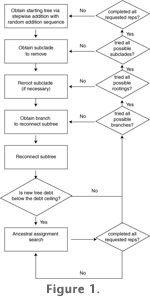 A more detailed description follows, but, in general, the tree search algorithm in StrataPhy consists of first constructing a starting tree, then rearranging it and simultaneously searching for optimal assignments of taxa as ancestors to find more optimal trees (Figure 1). After each rearrangement and assignment of ancestors, StrataPhy compares the debt of the new tree to the total debt of the optimal tree for the analysis so far. If the new tree has the same (optimal) debt it is saved for future swapping; if it has a lower debt, it is saved, and the old trees are deleted. StrataPhy then begins rearranging this new optimal tree. The search concludes when all rearrangements of all optimal trees have been made, without finding a more optimal one. A more detailed description follows, but, in general, the tree search algorithm in StrataPhy consists of first constructing a starting tree, then rearranging it and simultaneously searching for optimal assignments of taxa as ancestors to find more optimal trees (Figure 1). After each rearrangement and assignment of ancestors, StrataPhy compares the debt of the new tree to the total debt of the optimal tree for the analysis so far. If the new tree has the same (optimal) debt it is saved for future swapping; if it has a lower debt, it is saved, and the old trees are deleted. StrataPhy then begins rearranging this new optimal tree. The search concludes when all rearrangements of all optimal trees have been made, without finding a more optimal one.
The tree search algorithm of StrataPhy is essentially a tree bisection and reconnection (TBR) branch swapping routine (see
Swofford et al. 1996;
Felsenstein 2004 for a more detailed description), with modifications to include searches for the optimal assignment of taxa as ancestors. StrataPhy constructs the initial starting tree using a random stepwise taxon addition sequence (Swofford et al. 1996;
Felsenstein 2004), sequentially adding randomly selected taxa in the optimal (most parsimonious, considering morphologic and stratigraphic debt) location on the growing tree, until all taxa are added (Figure 2.1). The starting tree is rearranged using TBR branch swapping, which begins by breaking the initial tree into two subtrees (Figure 2.2 and
2.3). One of the subtrees is then attached systematically to each possible branch of the other subtree (Figure 2.4). Each time the subtree is reattached, a new topology is created, and the search for the optimal assignment of ancestors begins (described below;
Figure 2.5), and the debt of the new tree is compared to the debt of the current optimal tree. When one subtree has been reattached to all possible branches of the other, the former is rerooted iteratively (Figure 2.6), and then tried on all branches on the latter subtree again.
 As mentioned above, once the starting tree has been rearranged via TBR, StrataPhy then searches for optimal assignments of taxa as ancestral to others. StrataPhy offers two types of ancestral assignment searches: exhaustive and heuristic. The exhaustive search tries every possible combination of taxa fixed as ancestors or as terminal taxa. This requires 2n combinations for each branch swap, where n is the number of taxa in the tree. It is therefore computationally intensive and very time consuming, but guaranteed to yield all optimal assignments of ancestral taxa. The heuristic ancestral assignment search is computationally faster because it excludes many possible combinations that are necessarily less optimal (i.e., increase debt). In this heuristic ancestor search algorithm, the lengths of the tree with a given taxon fixed as an ancestor and as a terminal taxon are compared. If the assignment as an ancestor increases the total debt, then no further combinations are attempted with that taxon fixed as an ancestor on that topology; the taxon is left as a terminal taxon, and the next taxon is tested. If it decreases total debt, the taxon is fixed as an ancestor, and the next taxon is evaluated; the combinations in which such taxa are not designated as ancestors are disregarded. It is possible that the assignment of a taxon as an ancestor incurs no additional total debt, either because the stratigraphic debt savings and the morphologic debt incurred are equal, or because they are both zero. In either event, the search continues on two separate trees with and without the taxon assigned as an ancestor. As mentioned above, once the starting tree has been rearranged via TBR, StrataPhy then searches for optimal assignments of taxa as ancestral to others. StrataPhy offers two types of ancestral assignment searches: exhaustive and heuristic. The exhaustive search tries every possible combination of taxa fixed as ancestors or as terminal taxa. This requires 2n combinations for each branch swap, where n is the number of taxa in the tree. It is therefore computationally intensive and very time consuming, but guaranteed to yield all optimal assignments of ancestral taxa. The heuristic ancestral assignment search is computationally faster because it excludes many possible combinations that are necessarily less optimal (i.e., increase debt). In this heuristic ancestor search algorithm, the lengths of the tree with a given taxon fixed as an ancestor and as a terminal taxon are compared. If the assignment as an ancestor increases the total debt, then no further combinations are attempted with that taxon fixed as an ancestor on that topology; the taxon is left as a terminal taxon, and the next taxon is tested. If it decreases total debt, the taxon is fixed as an ancestor, and the next taxon is evaluated; the combinations in which such taxa are not designated as ancestors are disregarded. It is possible that the assignment of a taxon as an ancestor incurs no additional total debt, either because the stratigraphic debt savings and the morphologic debt incurred are equal, or because they are both zero. In either event, the search continues on two separate trees with and without the taxon assigned as an ancestor.
In practice, the difference in debt when a taxon is fixed as an ancestor or as a terminal taxon is dependent on the ancestral status of taxa at surrounding nodes. The order in which taxa are tested as ancestors can change the effect the assignment has on total debt. To account for this, StrataPhy includes a user option that allows multiple random taxon addition sequences for testing taxa in ancestral positions, in a similar manner as when constructing the initial stepwise addition tree. In other words, for a single tree, several separate replicate attempts at fixing all taxa as ancestors can be performed, each with a different and random order in which taxa are evaluated. Multiple replicates increase the chances of the optimal assignment of ancestors being encountered, although, as in any heuristic algorithm, do not guarantee the optimal solution will be found.
Although faster than the exhaustive ancestral assignment search, the heuristic search is still computationally intensive. StrataPhy therefore employs a debt ceiling (Fisher 1992) to minimize the number of cladograms that are searched for optimal ancestors in this manner. When a single TBR search produces a new candidate topology that could be searched for optimal assignment of ancestors, StrataPhy determines the maximum stratigraphic debt savings possible for that candidate topology. If the difference between the total debt of the candidate topology (without fixed ancestors) and that of the globally optimal tree for the current search replicate is greater than the maximum possible stratigraphic savings, then the candidate topology cannot possibly be shorter than the optimal tree. In other words, the maximum debt savings possible by assigning taxa as ancestors could not possibly reduce the debt lower than the current optimal debt. At this point, StrataPhy abandons the ancestral assignment routine, and this topology is discarded. StrataPhy empirically determines the maximum possible stratigraphic savings with an algorithm that sequentially fixes as ancestors all taxa that save stratigraphic debt, without regard to morphologic debt incurred.
At the conclusion of each ancestral assignment search, the length of the current tree is compared to that of the best found over the entire search. As in other phylogenetic inference programs, if it is less than or equal to the best, it is saved, and a new round of TBR branch swapping begins on this new optimal tree. This amounts to a "hill-climbing" routine that swaps optimal trees until no better arrangements are found, discarding suboptimal ones along the way. The routine ends when the optimal trees cannot be rearranged to make more optimal ones. It is possible that single searches can become trapped on suboptimal "islands" (Maddison 1991), so StrataPhy includes the option for multiple replicate searches to better sample the tree space. As with heuristic cladistic searches, more replicates increase the chance that optimal trees will be found.
The stratigraphic data are inherently linearly ordered and irreversible, which is to say young ancestors cannot give rise to older descendants during the evolution of actual clades, although a given empirical data set with an incomplete fossil record might yield such hypotheses as most parsimonious. The
ordered and irreversible nature of the stratigraphic character means that when a stratigraphic character is included, StrataPhy must search rooted rather than unrooted networks. Searching rooted trees results in many more trees that must be considered, and therefore, even without searching for optimal ancestors, stratocladistic tree searching is considerably slower in StrataPhy than the cladistic searches in other available parsimony-based programs. When no stratigraphic character is included, trees are arbitrarily rooted on the first taxon in the matrix. If a stratigraphic character is included, the designation of an outgroup can significantly reduce the number of trees to be searched and correspondingly the analysis time. When outgroup taxa are specified, StrataPhy assumes that the optimal stratocladistic trees will be rooted on at least one of those taxa; StrataPhy will not consider trees in which ingroup taxa root the tree, no matter what their total debt. When no outgroup is specified, which is permissible within the logical framework of the stratocladistic optimality criteria, StrataPhy is forced to search all possible rootings of any candidate tree. Given that there are n-1 possible rootings of an unrooted tree with n taxa, each of which must be searched for optimal ancestor assignment in the absence of an outgroup, specifying an outgroup considerably reduces the possible analysis time. Specifying a single OTU as an outgroup saves time by allowing StrataPhy to skip the step of trying multiple rerootings of candidate trees produced during branch-swapping and therefore represents the fastest possible stratocladistic tree search.
The result of a phylogenetic analysis in StrataPhy is a NEXUS formatted text file containing the optimal trees. This tree file is most easily viewed using MacClade, because MacClade is currently the only program that graphically represents ancestral taxa. This tree file can therefore be used as the template for further studies of character evolution for which MacClade is intended (Maddison and Maddison 2005).
|