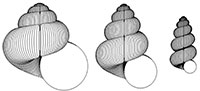
Heterochrony in helicoid spiral cones: a computer model for demonstrating heterochronic evolution
Article number: 18.1.2T
https://doi.org/10.26879/510
Copyright Palaeontological Association, April 2015
Author biography
Plain-language and multi-lingual abstracts
PDF version
Submission: 5 September 2014. Acceptance: 11 March 2015
{flike id=1120}
ABSTRACT
A modification of Raup’s classic helicoid logarithmic spiral cone model allows the incorporation of parameters for ontogenetic change in the main geometrical parameter values. The resulting allometric structures can be modified by simulated heterochronic increments so that the effects of neoteny, acceleration, progenesis and hypermorphosis can be produced. Experiments with the model, named HETEROSIM, produce suites of forms that are consistent with those that occur within Families of the Class Gastropoda, and hence heterochrony is a plausible hypothesis for evolution in those taxa. In addition to applications in evolutionary research, the model is a valuable pedagogic tool in teaching advanced palaeontology and evolution.
Andrew Robert Henry Swan. School of Geography, Geology and the Environment, Faculty of Science, Engineering and Computing, Kingston University, Penrhyn Road, Kingston upon Thames, Surrey KT1 2EE, United Kingdom swan@kingston.ac.uk
Keywords: Heterochrony; computer model; morphospace; gastropods
Final citation: Swan, Andrew Robert Henry. 2015. Heterochrony in helicoid spiral cones: a computer model for demonstrating heterochronic evolution. Palaeontologia Electronica 18.1.2T: 1-11. https://doi.org/10.26879/510
palaeo-electronica.org/content/2015/1120-gastropod-heterochrony-model
INTRODUCTION
In heterochronic evolution, ancestor and descendent differ in the rate and/or timing of ontogenetic change (Gould, 1977; Alberch et al., 1979). This mode of evolution has been postulated as important in all groups of organisms, with case studies based on palaeontological evidence involving trilobites, gastropods, ammonites, plants, rodents and primates (see, for example, McKinney, 1988). This paper focusses on molluscan shell shapes, which have often been the subject of heterochronic interpretations: for example work by Gould (1969), Tissot (1988), Allman (1994) and Seuss et al. (2012) makes it clear that heterochrony is significant in gastropod evolution; and papers by Swan (1988), Hammer and Bucher (2005) and Gerber (2011) demonstrate heterochrony in shelled cephalopods. However, modelling of molluscan shells has been dominated by the helicoid logarithmic spiral cone model of David Raup (1966). Raup’s simulations, as a consequence of the logarithmic model, are isometric: there is no change in the shape parameters during ontogeny. Consequently, heterochrony applied to such forms cannot result in evolutionary change in shape. This paper demonstrates the effect of heterochronic modes on an allometric model in which the parameters of a helicoid spiral cone vary through ontogeny. Experiments with the computer model, named HETEROSIM, show that a range of forms, especially of terrestrial gastropods, are consistent with a heterochronic origin, and the model can be used as a pedagogic tool to demonstrate heterochronic modes.
HETEROCHRONIC MODES
Alberch et al. (1979) rationalised the terminology of heterochronic modes as follows:
Paedomorphosis. The adult form of the descendant resembles the juvenile form of the ancestor. This can result from neoteny, where the rate of ontogenetic morphological change is slower in the descendant, or by progenesis, where ontogenetic change terminates early (often accompanied by early attainment of sexual maturity and short life spans).
Peramorphosis. The juvenile form of the descendant resembles the adult form of the ancestor, and the adult form of the descendant results from extrapolation of ontogenetic trends. This can result from acceleration, where the rate of ontogenetic morphological change is faster in the descendant, or by hypermorphosis, where ontogenetic change continues for a longer time.
Proportioned dwarfism and gigantism. Here the ontogenetic shape change is unaffected by evolution; ancestor and descendant differ in terms of size only. These modes can be modelled by scale change alone; this is mundane and is not further considered here. However, note that size change accompanying shape change is a common consequence of paedomorphic and peramorphic evolution.
MODELLING MOLLUSCAN SHELLS
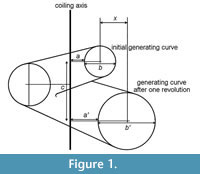The discovery that shells such as those of Nautilus can be modelled by logarithmic spirals dates back at least to the eighteenth century. Although measurement and analysis were used subsequently to demonstrate logarithmic spirals in a variety of molluscs, it was Raup’s (1966) work that allowed the wider recognition of many molluscan (and brachiopod) shells as helicoid logarithmic spiral cones. Raup isolated four parameters that defined such structures (refer to Figure 1):
W : Whorl expansion rate (ratio of whorl diameters separated by one rotation about the coiling axis):
W = b'/b 1
D: Diameter of umbilicus (as a proportion of total diameter):
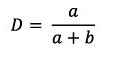2
S : Whorl shape (elliptical ratio: diameter parallel to coiling axis divided by diameter perpendicular to coiling axis).
T : Whorl translation (distance centre of whorl translates parallel to coiling axis in one rotation, divided by increase in distance of centre of whorl from coiling axis):
T = c/x 3
In the current study, a modification of the “whorl translation” parameter is used; this will be symbolised by T’:
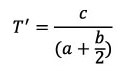4
(distance centre of whorl translates parallel to coiling axis in one rotation, divided by distance of whorl centre from coiling axis).
Raup’s T has the attractive property that all shapes with the same T have the same apical angle, regardless of the value of W. However, this is achieved by connecting the two parameters, as x is dependent on W. In heterochronic studies, it is useful to treat separate attributes as independent, or dissociated, from each other, at least in principle. So, we can regard the two attributes here as “expansion” and “translation”, rather than, effectively, “expansion” and “apical angle” in Raup’s formulation. As we will see in the experiments documented below, the use of T ’ rather than T allows the modelling of forms that occur in nature in which whorl expansion ceases through ontogeny, while translation continues.
The four “Raupian” parameters define a parameter space (“morphospace”) in which can be recognised separate (or partially overlapping) regions of occupancy by members of molluscan classes Cephalopoda, Gastropoda and Bivalvia, and members of phylum Brachiopoda. This model has been found to be applicable, at least approximately, to many extant and fossil molluscan and brachiopod shells (Swan, 1999, 2001), and has been the basis of models that add further parameters, for example aperture orientation (Noshita et al., 2012). “Raupian” shapes are isometric, and hence shells fitting this model do not change shape with growth. Although this might seem to be a reasonable pattern of growth, reflecting perhaps an unchanging mode of life through ontogeny, it is in fact surprising, as animals typically do change their mode of life in ontogeny (e.g., they may occupy different niches and exploit different food sources), and even a consistent mode of life might demand allometric changes in response to physical effects of inevitable area:volume ratio changes.
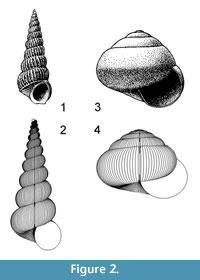
A property of “Raupian” shapes that assists in their recognition is that, in a profile view (perpendicular to the coiling axis), a straight line can be found that is tangential to all whorls (Figure 2.1-2).
Allometric growth in molluscs has been recognised by analysis of ammonites (e.g., Kant and Kullman, 1978) and is easy to observe in many gastropods, especially terrestrial forms (Figure 2.3-4). Allometric computer models have consequently been developed by several authors. Okamoto (1988a) used Frenet moving frame analysis, which allows an elliptical frame to move and expand freely in three dimensional (3D) space, with parameters for expansion, torsion and curvature that have values that can change continuously. Any arbitrarily curved tube or cone can be modelled. Okamoto (1988b) used this approach to great advantage in hydrostatic modelling of heteromorph ammonites, as the method facilitates calculation of centres of buoyancy and gravity. A difficulty of the method is the intricacy involved in finding the complete ontogenetic series of parameters that best represents an actually occurring form. Rice (1998) and Hammer and Bucher (2005) introduced models where movement of the generating curve is determined by vectors on its perimeter; these are also models with high-dimensional parameter space. Rice (1998) demonstrated that change in rate of shell production (which could be heterochronic) could explain substantial evolutionary change in gastropod morphology. Hammer and Bucher (2005) were able to demonstrate allometric changes in ammonite apertures that could be subject to heterochronic change.
The allometric model used here is relatively simple (with low parameter dimensionality) and is based on Raup’s model, but with four parameters (W, D, S and T’) permitted to change linearly. For the purposes of the present paper, only W and T’ are subject to ontogenetic change. The additional parameters are ΔW and ΔT’. W and T’ therefore function merely as the initial values; they will be distinguished as W0 and T’0. If the radius of the i th whorl is bi, then in Raup’s model:
bi= Wbi -1 5
whilst in the current model:
bi = (W0 + i ΔW) bi-1 6
Similarly, in an isometric model the amount of translation in one rotation ci is given by:
7
whilst in the current model:
8
There is no intention here to justify this model as a valid model of growth of molluscan shells. It remains uncertain how the genetics that control molluscan growth correlate with the form of the final adult shell, or how variation in shell geometry relates to genetic variation (this has been discussed by Rice [1998] and Urdy and Chirat [2006]). The organism will probably not have suites of alleles that correlate with such geometrical parameters. Indeed, although the coiling axis of gastropod shells seems to be a fundamental feature (it is readily locatable and is straight with remarkable consistency), molluscs presumably aren’t “aware” of, and don’t refer to, the coiling axis when growing and secreting shells. Rather, the model is intended here to quantify in an approximate way ontogenetic change similar to that observed in real organisms, and then to experiment with simulated heterochrony, making predictions of morphologies that may result.
MODELLING HETEROCHRONIC EVOLUTION
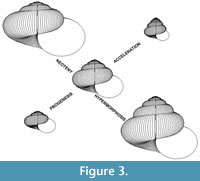Using the above model, “descendants” can be derived from “ancestors” through simulated heterochronic modes as follows:
Progenesis. Reduce the number of revolutions about the coiling axis. The default reduction offered by the computer program is one revolution.
Neoteny. Slow the rate of ontogenetic shape change by reducing ΔW and ΔT’. The default change offered by the computer program is x 3/4.
Hypermorphosis. Increase the number of revolutions about the coiling axis. The default increase offered by the computer program is one revolution.
Acceleration. Increase the rate of ontogenetic shape change by increasing ΔW and ΔT’. The default change offered by the computer program is x 4/3.
Figure 3 shows the range of “descendants” that are simulated from an example allometric “ancestor” by one increment of each of the above modes.
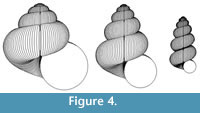
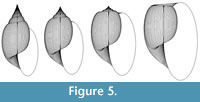
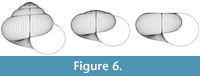
The scope for experimentation with the model is infinite, and different parameters of the “ancestor” yield a variety of often surprising heterochronic “descendants”. Figure 4, Figure 5, and Figure 6 show some illustrative examples.
 |
 |
 |
DISCUSSION
Hypotheses for Heterochronic Evolution
The pattern of diversity among allometric gastropods, especially Pulmonata, is generally consistent with the range of forms that can be simulated by heterochronic change applied to typical shell shapes. For example, Figure 4 shows that the curious narrowing of the final whorls in fusiform and pupaeform gastropods can be predicted on the basis of evolutionary acceleration of negative ontogenetic change in whorl expansion and positive ontogenetic change in whorl translation (these ontogenetic trends being typical of “conservative” Pulmonata). However, this evolutionary change is certainly not thereby proved, because: 1) no attempt is made here to demonstrate these trends in actual phylogenies; and 2) many actual gastropods have more complex ontogenetic changes than are rendered by the model described here. It should also be noted that Rice (1998) derived pupaeform geometries by reducing the rate of aperture expansion relative to shell production rate. A definitive analysis would involve the comparison of carefully measured empirical ontogenies between known ancestors and descendants. Nevertheless, modelling experiments such as those described here are useful in developing ideas and formulating hypotheses that could then be tested with empirical data.
The demonstration of the wide range of forms that can be derived by increments of various heterochronic modes raises an important question: if real gastropods have evolved such shapes by heterochrony, are the morphologies an incidental outcome of selection for the heterochronic mode, or is heterochrony the means by which a species “finds” a favourable morphology? It is clear that alleles for earlier or delayed sexual maturity may be selected under certain circumstances, and, in allometric forms, these will produce progenetic or hypermorphic descendants, respectively. Gould (1977) argued for “ecological correlates” of heterochronic modes, and, for example, connected progenesis with exploitation of ephemeral resources. If this is the principal “driving force” of evolution for a particular species at a particular time, then the adult morphology of the resulting descendant will be determined only by the ontogeny of the ancestor, and not by the performance of that morphology in the environment. To take the case of Melo in Figure 5, the shape might be an inadvertent consequence of selection for large size, effected via selection on alleles for faster rate of ontogenetic development. Alternatively, it could be that selection on the adult morphology is paramount, and this is attained, perhaps parsimoniously, by heterochronic exploitation of ontogenetic trends; hence, in Melo, acceleration might merely be the means by which a functionally favourable shape has evolved (with perhaps a low drag coefficient suitable for high-energy environments). It is certainly the case that ontogenetic allometry affords species the opportunity of the latter evolutionary route.
Pedagogic Applications
The demonstration of heterochrony is problematic in teaching palaeontology and evolution. Putative case studies are valuable but are not always convincing, because: 1) students need to observe and compare the ontogeny of ancestors and descendants, and clear illustrations are seldom available: and 2) theoretical models of what heterochrony would be predicted to produce are usually missing. Textbooks typically use illustrations of abstract morphologies in which arbitrary features join the ontogenetic sequence (the earliest being figure 7 in Gould, 1977). The current model can be used as a heuristic demonstration of the theoretical potential of heterochronic change, and students can compare simulations with real organisms as a first stage in assessing the validity of the heterochronic hypothesis. The author has used the model (in the form of the program HETEROSIM - available for download) in practical sessions in modules on palaeontology and evolution, and has supervised project work in which the program has been a key tool. Student feedback has been positive. Suggestions and advice on using the program are presented in Appendix 1, and a “screenshot” of the HETEROSIM program is presented in Appendix 2.
ACKNOWLEDGEMENTS
The author is grateful for constructive criticism from the anonymous reviewers, which has resulted in significant improvements to this paper.
REFERENCES
Alberch, P., Gould, S.J., Oster, G.F., and Wake, D.B. 1979. Size and shape in ontogeny and phylogeny. Paleobiology, 5:296-317.
Allman, W.D. 1994. Patterns and processes of heterochrony in Lower Tertiary turritelline gastropods, U.S. Gulf and Atlantic coastal plains. Journal of Paleontology, 68:80-95.
Anon. 1975. British Caenozoic Fossils. Natural History Museum, London.
Gerber, S. 2011. Comparing the differential filling of morphospace and allometric space through time: the morphological and developmental dynamics of Early Jurassic ammonoids. Paleobiology, 37:369-382.
Gould, S.J. 1969. An evolutionary microcosm: Pleistocene and Recent history of the land snail Poecilozonites in Bermuda. Bulletin of the Museum of Comparative Zoology, 138:407-532.
Gould, S.J. 1977. Ontogeny and Phylogeny. Harvard University Press, Cambridge, Massachusetts.
Hammer, O. and Bucher, H. 2005. Models for the morphogenesis of the molluscan shell. Lethaia, 38:111-122.
Kant, R. and Kullman, J. 1978. Gehause-Allometrie bei Cephalopoden. Neues Jahrbuch für Geologie und Paläontologie, 157:98-103.
McKinney M.L. (ed.) 1988. Heterochrony in Evolution: A Multidisciplinary Approach. Springer, New York.
Noshita, K., Asami, T., and Ubukata, T. 2012. Functional constraints on coiling geometry and aperture inclination in gastropods. Paleobiology, 38:322-334.
Okamoto, T. 1988a. Analysis of heteromorph ammonoids by differential geometry. Palaeontology, 31:35-52.
Okamoto, T. 1988b. Changes in life orientation during the ontogeny of some heteromorph ammonoids. Palaeontology, 31:281-294.
Raup, D.M. 1966. Geometric analysis of shell coiling: some general problems. Journal ofPaleontology, 40:1178-1190.
Rice, S.H. 1998. The bio-geometry of mollusc shells. Paleobiology, 24:133-149.
Seuss, B., Nützel, A., Scholz, H., and Frýda, J. 2012. The Palaeozoic evolution of the gastropod larval shell: larval armour and tight coiling as a result of predation-driven heterochronic character displacement. Evolution and Development, 14:212-228.
Swan, A.R.H. 1988. Heterochronic trends in Namurian ammonoid evolution. Palaeontology, 31: 1033-1052.
Swan, A.R.H. 1999. Computer models of invertebrate morphology, p. 157-179. In Harper, D.A.T. (ed.), Numerical Palaeobiology. Wiley, Chichester.
Swan, A.R.H. 2001. The occupation of morphospace, p. 157-161. In Briggs, D.E.G. and Crowther, P.R. (eds.), Palaeobiology II. Blackwell Science, Oxford.
Tissot, B.N. 1988. Geographical variation and heterochrony in two species of cowries (Genus Cypraea). Evolution, 42:103-117.
Urdy, S. and Chirat, R. 2006. Snail shell coiling (re-)evolution and the evo-devo revolution. Journal of Zoological Systematics and Evolutionary Research, 44:1-7.
