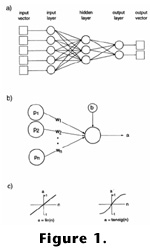Among
the several ANN learning algorithms available, BP is the most popular (Figure
1A). The BP network consists of an interconnected series of layers, each
containing a number of processing units called `neurons' (Figure
1B). The basic steps in our application of the BP network are: (1) training
of the network on the basis of a number of training sets, and (2) assessment of
the performance of the network by computations of the error rates in the test
sets (details are given below).
The main steps in the neural network procedure are as follows: the input signals (e.g., nannoplankton relative abundances), enter the network via the input layer; each neuron in the network processes the input data, with the resulting values steadily seeping through the network layer by layer, until a result is generated in the output layer. The output of the network is then compared with the actual output value. This results in an error value, representing the sum-squared difference between the actual and predicted input. In order to minimize this error value all the weights at each connection of the network are gradually adjusted in the direction of the steepest descent with respect to the error (the steepest-descent algorithm). This process involves working backwards from the output layer, through the hidden layer, and back to the input layer, until the specified error limit is reached. Fine-tuning the weights in this way has the effect of `teaching' the network how to produce the `desired' output for a particular input. In this way the network `learns'.
The last three steps described above usually have to be repeated a number of times until the error value is minimized (in the ideal case this error is zero). These steps may potentially involve many thousand training passes. This iterative process is the kernel of the back propagation algorithm. Finally, when the network has converged (meaning, reached a preset error limit), it will ideally be able to produce the correct output for each input. Once the network has been trained, it can be used to predict the output signals used in the training phase from new input signals.
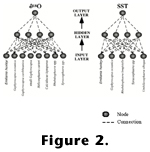In
the analysis of the dataset from the California Bight, we used five neurons in
the input layer (corresponding to the five species of nannoplankton used as
input variables). In the Mediterranean dataset, we used eight neurons in the
input layer. In both cases, the number of neurons in the output layer is one
(corresponding to the SST and oxygen isotope data to be predicted; Figure
2). The software used was the NeuroGenetic Optimizer (NGO), version 2.6,
from BioComp Systems,
Inc.
This program automatically attempts either one or two hidden layers to find the optimum network. The program also allows the number of network cycles to be specified prior to the start of the data processing. Each of these cycles utilizes a different network configuration. The cycles are divided into populations and generations that can both be varied. In addition, the program searches the best solution by varying the different number of neurons in each of the different layers. The NeuroGenetic Optimizer attempts different types of transfer functions within single neurons (linear, logarithmic and hyperbolic tangent) when performing genetic searches.
