A biplanar X-ray method for three-dimensional analysis of track formation
Article number: 16.1.1T
https://doi.org/10.26879/324
Copyright Palaeontological Association, January 2013
Author biographies
Plain-language and multi-lingual abstracts
PDF version
Submission: 14 April 2012. Acceptance: 4 January 2013
{flike id=371}
ABSTRACT
Tracks arise through a complex interplay between animal and substrate. Studying this dynamic process is challenging because most foot-sediment and sediment-sediment interactions are rapid and hidden from view. Herein, we describe a new method for visualizing and quantifying three-dimensional movements of both a morphologically accurate indenter and realistic sediment during track formation. Our method uses biplanar X-ray imaging and an animation-based workflow to reconstruct the trajectories of metal beads seeded throughout the sediment volume. X-rays allow sub-surface motion normally concealed by the foot and opaque matrix to be analyzed at 30 frames per second with sub-millimeter resolution. Results from two case studies of tridactyl tracks in semi-liquid mud provide novel, animated visualizations, examples of ensemble and particle-specific data, as well as measures of precision and accuracy. This methodology has the potential to mechanistically link specific track morphologies to foot movement, clarify undertrack formation, validate computational models, and set a new standard for evidence-based reconstruction of locomotion from fossil footprints.
Richard G. Ellis. Department of Ecology and Evolutionary Biology, Brown University, Providence, Rhode Island, USA
and
Structure and Motion Lab, The Royal Veterinary College, Hawkshead Lane, North Mymms, Hatfield, Hertfordshire, AL9 7TA, United Kingdom
Stephen M. Gatesy (correspondence author).Department of Ecology and Evolutionary Biology, Brown University, Providence, Rhode Island, USA
Keywords: track formation; three-dimensional motion analysis; experimental methods; X-ray; foot kinematics
Final citation: Ellis, Richard G. and Gatesy, Stephen M. 2013. A biplanar X-ray method for three-dimensional analysis of track formation, Palaeontologia Electronica Vol. 16, Issue 1; 1T, 16p. https://doi.org/10.26879/324
palaeo-electronica.org/content/2013/371-x-ray-track-analysis
INTRODUCTION
Many tetrapod tracks form as the foot plunges into, moves through, and withdraws from the substrate. Track morphology can be further altered by subsequent settlement, compression, and erosion. Given that the ichnological record preserves only a final snapshot of this entire process, reconstructing details of foot kinematics from fossil tracks remains a complex problem. Such difficulty is amplified for deep tracks, as the relationship between foot movement and sub-surface track morphology is still poorly understood.
We seek to explore a fundamental question in ichnology: how do sedimentary particles move from their starting locations in untrod ground to their ultimate resting places? Our goal is to develop a method to follow the three-dimensional trajectory of individual particles within a substrate volume during track formation. A technique that can relate sediment displacement, both spatially and temporally, to the moving foot throughout a step would help reveal the origin, modification, and interaction of specific track features, as well as their usefulness for motion reconstruction.
Experimental studies using layered clay, sand, cement, and plaster have revealed basic patterns of sub-surface deformation created by simple punches (Allen, 1989, 1997), more realistic foot models (Manning, 2004; Jackson et al., 2009, 2010), and severed feet (Milàn and Bromley, 2006, 2008). Such approaches are well suited for documenting the distortion of interfaces between layers, but are unable to discern the displacement of sediment within each layer (Gatesy, 2003). Indented arrays of square Plasticine prisms have provided additional detail (Allen, 1997), but spatial resolution remains limited. All of these methods involve opaque materials that require destructive sectioning or splitting, which precludes dynamic analysis of the sequence of track formation.
Herein, we describe the novel application of biplanar X-ray video to study footprints. Hardware and software tools originally created for capturing three-dimensional skeletal motion (Brainerd et al., 2010; Gatesy et al., 2010) are applied to reconstruct both foot movement and particle trajectories during track development. We present results from two case studies using artificial mud laced with metal beads, which serve as markers. In the first, a rigid cast model mounted on a linear actuator was repeatedly plunged down and forward into the sediment. In the second series, a cadaver turkey foot was manipulated to emulate a more realistic stepping motion. We report the X-ray system's accuracy and precision for tracing three-dimensional kinematics, present examples of the novel data that can be acquired, and discuss the strengths and weaknesses of the method.
METHODS
Overview
Our general approach involves animating the three-dimensional trajectory of radio-dense beads seeded in a volume of sediment using two (biplanar) X-ray beams oriented approximately 90° apart. Following distortion correction and calibration, "virtual cameras" are created with the three-dimensional animation software Maya 2010 (Autodesk, Inc.) so that paired video frames can be viewed from the perspectives of the real X-ray sources. Digital bead models are aligned to their corresponding images in each frame and used to reconstruct three-dimensional trajectories of sediment markers as well as the position and orientation of the indenter. Such animations serve as accurate visualizations of track formation and provide the raw data for quantitative analysis.
X-ray Hardware, Settings, Distortion Correction, and Calibration
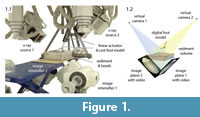Video recordings were made in the W.M. Keck Foundation XROMM Facility, a custom-built biplanar X-ray room at Brown University (Figure 1.1). The facility contains two X-ray generation and recording systems, each of which consists of an EMD Technologies model EPS 45-80 pulsed X-ray generator, a Varian model G-1086 X-ray tube suspended from the ceiling on a telescoping crane, a Dunlee model TH9447QXH590 image intensifier (40.64 cm diameter) mounted on a mobile-arm base, and a Phantom v9.1 high-speed digital video camera. The imaging chain achieves an overall resolution of approximately 2.3 line pairs/mm.
Two X-ray beams were oriented downward at approximately +45° and -45° from vertical to intersect at the sediment volume. Source to image distances were 96 cm and 105 cm. A 30 Hz pulsed beam (5 ms duration) of 110 kV and 320 mA produced images that were recorded at 1808x1800 pixel resolution and 30 fps with an exposure time of 700 μs. These X-ray energies were higher than those used in traditional skeletal recordings, but were required to penetrate the dense sediment mixture. All trials were also recorded from above using a high definition video camera (Sony Handycam HDR-FX1; 30 fps) to document the exposed indenter and sediment surface.
We employed a workflow created for three-dimensional skeletal motion analysis (marker-based X-ray Reconstruction of Moving Morphology or XROMM, described in Brainerd et al., 2010 and at xromm.org) for initial processing steps, which we describe here briefly. First, X-ray hardware and video camera distortion was corrected based on images of a standardized metal grid. Second, the volume of X-ray overlap was calibrated using an acrylic cube bearing 64 steel beads (3 mm diameter). Using the 2-D bead coordinates in each undistorted image and the cube's known geometry we calculated the relative position and orientation of each X-ray source by direct linear transformation (Hedrick, 2008). We next imported X-ray source coordinates and rotations into Maya software to create two "virtual cameras" and two image planes, which display sequences of undistorted video frames as animated textures (Figure 1.2). When viewed through each reconstructed camera, a user has the same perspectives as the X-ray beams, as if viewing the scene with X-ray vision.
Sediment and Marker Beads
A dry mix of silica flour (56 wt%, grain size <120 μm), sand (40 wt%, <1 mm), and ball clay (4 wt%) was hydrated with 24 ml of water per 100 g to form a wet, sloppy mud. We chose this specific mixture to approximate the consistency of sediment preserving deeply impressed Late Triassic theropod footprints from Greenland (Jenkins et al., 1994; Gatesy et al., 1999; Gatesy, 2003). Six cm of sediment was filled into a 47x27 cm, radio-translucent, flat-bottomed plastic tray, which was suspended in the X-ray field between two hydraulic scissor lifts (Figure 1.1).
Metal beads (2 mm diameter lead chilled shot; Ames Metal Products, Corp., Chicago, IL, USA) were introduced at the surface beneath the indenter and served to trace sediment displacement. The beads gradually became distributed throughout the volume by indenter action during each trial and by sediment mixing and smoothing between trials. The number of beads visible in both cameras varied across trials (see below). A triad of larger, 3 mm diameter beads from the same manufacturer was taped to the bottom of the tray to provide a fixed lower reference that could be easily distinguished from the free sediment beads.
Indenters
As a proof of concept for the biplanar X-ray approach, we sought a biologically realistic indenter that would resemble the foot of Mesozoic theropods responsible for deep tracks in Greenland (Jenkins et al., 1994; Gatesy et al., 1999) and the Connecticut Valley (Hitchcock, 1858, Rainforth, 2005). Rather than sculpting a model based on fossil material, we used the severed right foot of a male turkey, in accordance with previous emu experiments (Milàn and Bromley, 2006, 2008).
Case Study 1: Repeatable Plunge Trials
For our first series of recordings, we created a rigid cast turkey model to simplify foot kinematics as much as possible. To more closely approximate the inferred primitive theropod condition (Gatesy et al., 1999; Padian, 2003), we wired the severed turkey foot to a foam block with the tarsometarsus raised 30° above the plane of the toes and the hallux pointed anteromedially. The foot was then frozen, molded in silicon putty (Knead-A-Mold, A2Z Solutions), and cast with polyurethane (Por-A-Kast Mark 2; Synair Corp.). To calculate rigid body kinematics, we marked the plastic foot cast with four lead beads (3 mm diameter) secured with cyanoacrylate adhesive into drilled pits in the dorsal surface near the base of tarsometatarsus, midway along digit II, and on the claws of digits III and IV. We further modified the cast by removing the metatarsal spur and trimming the interdigital webbing. We created a digital copy using a MicroScan3D laser sensor system mounted to a MicroScribe MLX articulated arm (RSI, Oberursel, Germany) to collect a point cloud and form a polygonal model. In Maya software, we hand fit sphere models to the locations of the polygonal foot mesh representing each implanted bead.
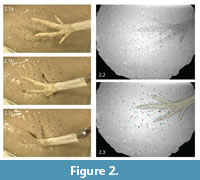
We plunged the foot model into the sediment at 39° below horizontal to within 1.5 cm of the bottom using an electric linear actuator (20.3 cm travel; McMaster-Carr) mounted on a rigid metal frame (Figure 1.1, Figure 2.1). Approximately 50 beads (2 mm diameter) were placed on the mud's surface in the first trial. We conducted a total of 14 trials, adding beads between sequences to reach a maximum of approximately 190 markers, not all of which appeared in both X-ray videos.
Case Study 2: Full Motion Trials
For our second series of recordings, the intact foot was manipulated through the sediment with a more realistic motion pattern. To increase X-ray visibility in the dense substrate, we implanted 3 mm markers in the proximal/distal tarsometatarsus, spur, and ungual of each digit, as well 2 mm diameter beads along the length of digits II-IV. We recorded two artificial tracks by simulating both foot entry and withdrawal using the thawed cadaver turkey foot. A long wooden dowel firmly fastened to the tarsometatarsus allowed us to manipulate the foot by hand from a safe distance above the X-ray field. We manually spread the toes, plunged the foot down and forward into the sediment, and rotated the tarsometatarsus prior to withdrawal. We mimicked stance flexion and toe convergence during liftoff by applying tension to the flexor digitorum longus tendon with a stiff, braided string and surgical hemostat (Gatesy et al., 1999).
Bead and Foot Animation
Calibration of the three-dimensional space allows the creation of virtual cameras in Maya animation software that match the relative positions and orientations of the X-ray beams in the real world. By viewing undistorted pairs of video frames from these perspectives, we reconstructed each bead's three-dimensional position by rotoscoping. Rotoscoping entails simultaneously aligning or registering a digital sphere model to its two X-ray shadows (Figure 2.2, 2.3; as described in Gatesy et al., 2010). We saved or "keyed" each model's XYZ coordinates for multiple frames. Maya software automatically interpolates between these keyframes to form a continuous animation. Not every frame required registration; keyframes could be widely spaced in periods of bead stasis.
We animated the cast foot using the coordinates of its four embedded beads, which were exported to calculate the rigid body kinematics of the bead cluster. Three translations and three rotations computed by singular value decomposition (Söderkvist and Wedin, 1993) were applied to the digital foot model (Brainerd et al., 2010). For the repeatable series, the consistent motion of the linear actuator permitted us to combine data from the 14 plunges. We temporally aligned each trial and then imported all foot and bead animations into a single animation that summarized the plunge results. For the full step trials, we animated the 11 foot markers and linked them together with cylinders to create a simplified stick representation.
RESULTS
Field of View, Precision, and Accuracy
In our specific configuration, the two conical X-ray beams (Figure 1) intersected to form a biplanar volume totaling ~18000 cm3 (Beyer et al., 1987). Of this, sediment filled a roughly rectangular region 22 cm long, 27 cm wide, and 6 cm deep, resulting in ~3600 cm3 of sediment imaged by both cameras for three-dimensional analysis.
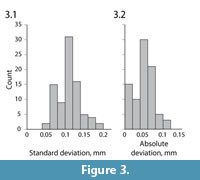
To validate the biplanar X-ray approach to particle analysis, we used four different metrics to ensure that reconstructed bead positions through time reflect true three-dimensional motion. As a whole, the distributed sediment markers do not have a fixed or know geometry, but the spatial relationship among the four beads embedded in the cast foot remained constant in repeatable trials. We therefore calculated six inter-bead distances at each of the first 65 frames of the 14 repeatable plunge trials. Within each trial, the standard deviation in distance between any two foot beads averaged only 0.11 mm (Figure 3.1). Moreover, across all 14 trials the average inter-bead distance from each trial was within 0.12 mm of the group mean (Figure 3.2). Together, these suggest that inter- and intra-trial variability were less than ~0.12 mm for our setup and analysis method under dynamic conditions. These findings are consistent with those of Miranda et al. (2011) for this hardware system.
To test that the X-ray method did not introduce a systematic bias, we measured inter-bead distances among the model foot beads 10 times with standard electronic calipers. We compared these measurements to the average distance between any two markers across our 14 trials average (Table 1). Although inter-bead distances ranged from ~35 mm to ~91 mm, the two measurement techniques yielded results within 0.3 mm in all cases, which is comparable to our caliper resolution (± 0.29 mm). Finally, we evaluated overall system accuracy using images of the calibration cube. Under ideal conditions, the specified three-dimensional coordinates of the actual cube beads should correspond exactly to those of our X-ray reconstruction. Any difference represents compound errors associated with imperfect distortion removal, camera calibration, model registration, and cube fabrication. We found that the mean three-dimensional offset between real and animated cube positions was 0.13 mm.
Case Study 1: Repeatable Plunge Trials
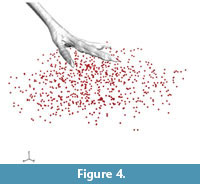In this series, a linear actuator drove the rigid cast foot model into the sediment along a fixed, diagonal path (Figure 1.2, Figure 2.1). Sediment markers from all 14 trials combined to a total of 810 animated beads (Figure 4) at an aggregate density of one per ~4.4 cm3 within the biplanar sediment volume. Our addition of new beads to the surface directly beneath the foot cast increased the resolution within this 660 cm3 sub-volume of interest to an average density of one per ~1.9 cm3.
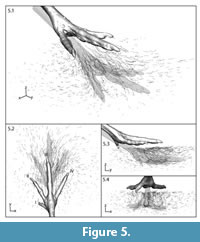For an overall picture, we depict the reconstructed three-dimensional paths of all 810 bead models as an ensemble displacement field (Figure 5). From their starting positions prior to foot contact, bead locations are shown every 33.3 ms for the 1.43 s interval sediment was in motion. Markers directly in the indenter's path exhibited the longest and most complex displacements; those far from the foot model (Figure 5.2) or very deep (Figure 5.3, 5.4) had limited movement. Markers beneath the foot were driven forward and down, while those in front moved forward and up (Figure 5.3). Only 242 of the 810 beads (~30%) showed net downward motion.
We next explore subsets of the complete dataset to address specific spatial and temporal aspects of track formation.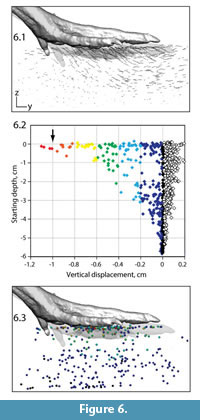
Figure 6 shows bead motion during the period in which the model's three main toes descend through the top 1 cm of sediment. In lateral view, bead paths showed a dramatic drop-off in length with starting depth (Figure 6.1). We can also quantify specific dimension during this interval. For example, plotting vertical displacement versus starting depth shows the steep gradient in maximum descent (Figure 6.2). Only a few shallow beads moved down as much as the indenter (arrow). Beads starting 3 cm below the surface mostly moved anteriorly, with maximum descent decaying to less than 3 mm. Markers near the bottom demonstrated almost no vertical change. We can also view this spatial pattern through differential coloring of beads in their positions prior to foot contact (Figure 6.3).
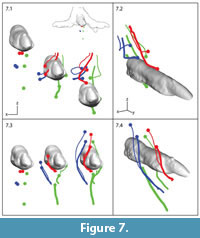Our method provides high resolution data, allowing us to examine the trajectories of specific particles of interest with respect to the indenter. Figure 7 shows anterior and perspective views of the distal end of digit III and seven markers that fall within its path, starting at the frame of sediment contact (Figure 7, leftmost). Beads began at the surface, ~9 mm deep and ~20 mm deep. Red and blue pairs started adjacent to each other horizontally, whereas green markers were vertically aligned at different depths.
Both initial depth and transverse position relative to the midline of digit III determined bead behavior. The descending foot cast drove all seven beads downward (Figure 7.1, 7.2), but only the deepest green bead remained below the model. Others were first pushed apart (Figure 7.1, left to middle) and then converged back above the digital midline (Figure 7.1, middle to right) along looping paths (Figure 4, Figure 5). Red and blue beads passed lateral to digit III (left in anterior perspective), whereas the two shallower green beads passed medially. Markers initially at the same depth but with different transverse positions ended up stacked almost vertically, with midline beads being driven deepest.
Local sediment deformation can also be visualized and interpreted in different reference frames. Figure 7.3 and 7.4 shows bead displacement in model space. Markers flowed along arcing trajectories up, around, and over the toe as if in a flume. More midline beads (thick red and blue paths) took longer to pass around the toe. Markers affected by the model's side toes (digits II and IV) showed a similar pattern to that observed in Figure 7, although the offset of each toe and penetration angle of the whole model resulted in a more diagonal plowing through the sediment.
Case Study 2: Full Motion Trials
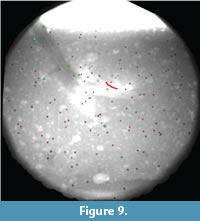We simulated a more complete step by manipulating an articulated turkey foot through both sediment entry and withdrawal (Figure 8). In the two trials, 96 and 108 beads were animated, resulting in densities of one per ~37 cm3 and ~33 cm3, respectively. Figure 9 presents results from the first of these trials.
We divide track creation into four phases based on foot and sediment movement: penetration, mid-stance, withdrawal, and collapse. During penetration, the foot entered the sediment and descended with toes spread (Figure 8a-b). Reconstructed motion reveals that the foot moved slower (4.47 cm/s) than during the repeatable trials, but at approximately the same angle (38° below horizontal).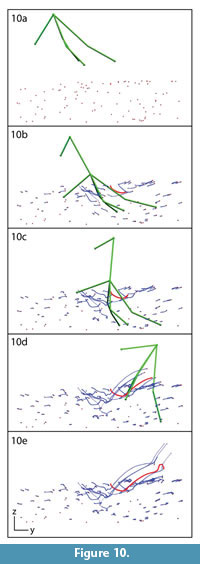 
Bead paths in this phase were also similar to those observed during the repeatable trials; beads near the foot were forced down and forward while more anterior beads shifted forward and upward (Figure 10a-b). Distant beads moved little. During mid-stance (Figure 8b-c), bead motion was quite limited; paths show little change from the end of penetration (compare Figure 10c with 10b).
During withdrawal (Figure 8c-d), sediment trapped above and between digits II-IV was lifted and dragged as the toes emerged. Several of the shallower beads were moved extremely long distances as they followed the rising foot (Figure 10c-d). Sediment and three markers remained stuck to the foot and were lifted away (Figure 8d, Figure 10e). The remainder collapsed back down as the track settled into its ultimate configuration (Figure 8e, Figure 9, and Figure 10e).
The bead highlighted in Figure 9 and Figure 10 exemplifies the most disturbed region of sediment. Figure 11.1 shows the complexity of its excursion in lateral view. 
This marker started ~3 mm below the surface and moved down, forward, and medially around digit III in the penetration phase. Little movement occurred during mid-stance, but as the foot was withdrawn the bead was lifted forward before collapsing to finish ~1.5 cm above the initial sediment surface. A plot of this bead's displacement through time shows major events within track formation (Figure 11.2). The bead traveled a total of 11.2 cm along a circuitous path, ending up 7.8 cm from its starting point.
DISCUSSION
We describe a novel method for studying foot-sediment and sediment-sediment interactions during track formation. Our immediate goal was to quantify how the substrate deforms during footfall at the level of sedimentary particles. Accurate animations integrating indenter and marker movement offer a unique perspective on the spatial and temporal nature of particle displacement throughout the genesis of a track. Ultimately, we wish to better understand deep, penetrative track morphologies (e.g., Hitchcock, 1858) and to use them to reconstruct foot movement during locomotion (Avanzini, 1998; Gatesy et al., 1999; Gatesy, 2003; Romero-Molina et al., 2003; Boutakiout et al., 2006; Perez-Lorente and Herrero Gascón, 2007; Ischigaki, 2010; Avanzini et al., 2011; Huerta et al., 2012).
Implications
As a preface, it is worth asking if a bead's displacement reasonably represents motion of the surrounding sediment. Lead has a much higher density than silica, yet we found no evidence of differential sinking. Newly added beads remained visible on the surface unless affected by the model. At a diameter of 2 mm, the marker beads were larger than the sand used in our matrix, but well within the grain size range for sediments in which tracks are recorded. At a very fine scale, beads may not have interacted with their neighbors or the indenter exactly like other particles. However, we believe that lead beads are suitable indicators of sediment motion for exploring track creation at a macroscopic level as done here.
Although, the aim of this study was to test and validate a new method of experimental track analysis, these preliminary results provide insight into general footprint formation mechanisms. For example, the transmission of undertracks to deeper bedding planes is central to understanding fossil specimens both in the field and in museum collections. In order to interpret a transmitted undertrack, we need to know not only how far its bedding plane was below the original tracking surface, but also how far it was below the maximum penetration of the foot. Our method makes it possible to quantify the foot's ability to influence distant particles. In our semi-liquid test sediment, maximum displacement decayed rapidly beyond ~1 cm below the model (Figure 6). Testing different sediment compositions and hydrations will reveal how transmission distance varies with rheology.
In especially deep tracks, such as many from the Late Triassic of Greenland (Jenkins et al., 1994; Gatesy et al., 1999; Gatesy, 2003) and Early Jurassic of the Connecticut Valley (Hitchcock, 1858; Rainforth, 2005), penetration is likely more important than transmission to undertrack formation. In both series of experiments, beads nearest the foot flowed around and over the penetrating digits before re-approximating to form sealed slits (Figure 2.1, Figure 5). Particles closer to the digital midline were dragged deeper (Figure 7), shearing the originally adjacent beads into a vertically offset arrangement. Although greater sampling is needed, such evidence clarifies the formation dynamics of the nested, V-shaped laminae characteristic of penetrative tracks (Olsen, 2002; Gatesy, 2003; Rainforth, 2005).
The more complete tracks made with the articulated turkey foot leave us optimistic about reconstructing motion from deep fossil tracks (Gatesy et al., 1999; Gatesy, 2003; Romero-Molina et al., 2003; Boutakiout et al., 2006; Perez-Lorente and Herrero Gascón, 2007; Ischigaki, 2010; Avanzini et al., 2011; Huerta et al., 2012). Foot withdrawal left obvious exit traces (Figure 8) similar to those seen in live birds and described from Greenland (Gatesy et al., 1999). In Figure 11 we emphasize the complex journey of one bead, but not all underwent such large movements. Many beads displaced during penetration were relatively unaffected by withdrawal (Figure 10), suggesting that evidence of all phases of ground contact can survive to enter the fossil record.
Advantages of a Biplanar X-ray Approach
The primary benefit of our method is the ability to study the three-dimensional dynamics of sub-surface phenomena normally concealed within an opaque matrix. In this we follow previous workers that used X-rays to image burrowing invertebrates (Howard, 1968; Charboneau et al., 1997; Gingras et al., 2008), fish (Gidmark et al., 2011), and lizards (Maladen et al., 2009). For footprints, however, our goal was to visualize and quantify motion of not only the organism, but also of the sediment itself. In both of our case studies, marker beads near the foot followed long and kinematically interesting paths that would not be accessible using traditional techniques. Knowing which sediment remains relatively undisturbed is equally important, as differential displacement is the essence of track formation.
Our animation-based approach also provides access to poorly understood temporal aspects of track formation dynamics. Destructive experimental studies provide only single snapshots of the creation process (Allen, 1989, 1997; Manning, 2004; Milàn and Bromley, 2006, 2008; Jackson et al., 2009, 2010). A layered substrate can be used once before being sectioned or disassembled, so a series of trials must be aborted at different stages to reconstruct a sequence (e.g., Allen, 1997). The X-ray method provides as much temporal resolution as desired. We recorded at 30 fps, but the video cameras connected to the image intensifiers are capable of rates as fast as 1000 fps if needed.
Biplanar X-ray studies also offer an unprecedented opportunity to validate computer simulations. As models of foot-sediment and sediment-sediment interactions become more and more sophisticated (e.g., Falkingham et al., 2009; Maladen et al., 2011), the need to ground-truth synthetic footprints becomes essential. Actual three-dimensional trajectories of sub-surface markers offer rich new data for evaluating simulated sediment displacements.
Caveats and Possible Solutions
Thorough characterization of sediment motion requires reconstruction of many, many bead trajectories. A major weakness of the method described here is the limited number of particles that can be traced simultaneously. For example, even our aggregate repeatable trials provide only a partial view of total sediment behavior. We believe that tracing a few hundred beads in one trial is possible, but analyzing higher numbers would likely remain problematic.
The primary limitation on bead number is visual interference during rotoscoping. In order to accurately animate a bead model in three-dimension, we need to be able to identify its X-ray shadow in both videos. At higher densities, ambiguity often arises when uncertain geometric relationships result in multiple possible pairings. Identification of peripheral beads that undergo very little motion is particularly difficult. In some cases we resolved conflicts by excluding erroneous reconstructions that would locate a bead outside the known sediment volume. We also mitigated this issue by recording the entire tray of matrix undergoing a small rotation, which introduces parallax that differentiates static beads. Another alternative is to use beads of different diameter or shape to help in the identification process.
Combining data from multiple trials raises marker density, but is only justified if the motion is highly reproducible as in the linear actuator series. Our total of 810 beads could easily be increased by doing more trials and having more beads per trial, thereby filling in areas left sparsely sampled (Figures 4, 5). Although simple, such repetitive movements may prove sufficient for many questions, particularly because the morphology and kinematics of the indenter can be as realistic as desired.
A second limitation is a lack of automation. For this study we rotoscoped each three-dimensional bead model by hand to pairs of video images for multiple frames. Although our animation speed increased with experience, this approach required a significant time investment. Solutions for automating bead identification and bead tracking that would assist, if not fully replace, a human animator in three-dimension reconstruction would be extremely valuable.
A third limitation is the size of the test volume. Image intensifiers set a limit on the maximum X-ray cone diameter for a single recording, which is ~40 cm in the W.M. Keck XROMM Facility. When an overlap zone is required for three-dimensional analysis, this volume shrinks down to about the size of a standard basketball. A system's X-ray energy also limits the maximum sediment depth. Because our 6 cm deep sample was imaged diagonally at close to 45°, the beams were passing through at least 8.5 cm. Creating sediment from less radio-dense components would allow deeper samples and lower energies, assuming that the desired rheology could be achieved.
Finally, the need for specialized hardware could render this technique inaccessible to many researchers. Pairs of refurbished hospital C-arm systems now cost ca. $140,000 US (Brainerd et al., 2010). We are aware of about a dozen systems primarily for zoological research and at least nine dedicated to human biomechanics; more are being installed and planned. Interested ichnologists could consider collaboration with colleagues in biomechanics/orthopaedics or zoology/paleontology to gain access to existing facilities and expertise.
Future Directions
Based on our two case studies, we believe that biplanar X-ray has great potential for unlocking previously hidden elements of track formation. One goal is to move beyond individual particle trajectories to fully characterize the entire volume. We have begun applying methods of three-dimensional interpolation to fill in the gaps between randomly distributed data points. Continuous functions will permit sampling of virtual undertracks at any depth, as well as slices in any other dimension during the genesis of a track.
We look forward to analyzing footprints made by live animals moving over and through an imaged sediment volume. In conjunction with existing methods for reconstructing skeletal movement (Brainerd et al., 2010; Gatesy et al., 2010), particle trajectories will document the link between foot kinematics and real track morphology. Live animals cannot be expected to make reproducible steps, so bead number will likely be limited. To achieve a denser sampling, articulated robotic feet could be used to generate consistent kinematic output for summation of separate trials. We also foresee improved documentation of the sediment surface through photogrammetry (e.g., Matthews et al., 2006; Falkingham, 2012). By generating a series of surface models during track formation, the trajectories of sub-surface particles can be visualized and analyzed within a more robust three-dimensional context.
Testing different rheologies and varying rheology with depth will provide quantitative data for understanding substrate effects on track morphology. However, our current approach is not amenable to surveying wide ranges of consistency, foot morphology, and foot motion. We believe that the greatest strength of biplanar X-ray imaging lies in its ability to ground-truth computer simulations. Once well-validated, the digital environment will be the better place to explore the many combinations of parameters involved in track formation.
Ultimately, we believe motion analysis using biplanar X-rays fosters a unique, particle-based perspective that has much to offer. Horizontal bedding typically limits ichnologists to studying surfaces at layer interfaces. Yet changes in layer thickness, depth, and shape only come about through the more fundamental spatial reconfiguration of their affiliated particles. Our approach records motion within each layer in all dimensions, not just depth, during track formation.
CONCLUSIONS
We describe a biplanar X-ray method for studying footprint formation dynamics using an animation-based workflow. Ensemble bead paths provide unprecedented visualization of the changing displacement field. The system's high accuracy and precision permits detailed, quantitative analysis of local, regional, and global sediment reconfiguration relative to the foot. By unlocking previously inaccessible dimensions of sediment motion, a particle-based approach generates crucial data for model validation, promotes a truly three-dimensional perspective of track formation, and provides novel insight into the genesis of track morphology.
ACKNOWLEDGEMENTS
We thank J. Whiteside and B. Brainerd for their advice and support, P. Falkingham for fruitful discussions, and two reviewers for critical comments. M. Dawson assisted throughout the X-ray procedures and K. Wellspring provided help with specimens in the Beneski Museum of Natural History, Amherst College. Supported by National Science Foundation grants IOS- 0925077 and DBI-0552051, the W.M. Keck Foundation, the Bushnell Family Research and Education Fund, and Autodesk, Inc.
REFERENCES
Allen, J.R.L. 1989. Fossil vertebrate tracks and indenter mechanics. Journal of the Geological Society London, 146:600–602.
Allen, J.R.L. 1997. Subfossil mammalian tracks (Flandrian) in the Severn Estuary, S.W. Britain: mechanics of formation, preservation and distribution. Philosophical Transcript of the Royal Society of London, 352:481–518.
Avanzini, M. 1998. Anatomy of a footprint: bioturbation as a key to understanding dinosaur walk dynamics. Ichnos 6:129–139.
Avanzini, M., Piñuela, L., and Garcia-Ramos, J.C. 2011. Late Jurassic footprints reveal walking kinematics of theropod dinosaurs. Lethaia 45:238–252.
Beyer, W.A., Fawcett, L.R., Mauldin, R.D., and Swartz, B.K. 1987. The volume common to two congruent circular cones whose axes intersect symmetrically. Journal of Symbolic Computation, 4:381–390.
Boutakiout, M., Hadri, M., Naouri, J., Caro, S., and Pérez-Lorente, F. 2006. The syngenetic structure suite of dinosaur footprints in finely laminated sandstones: site n°1 of Bin el Ouidane (1BO; Central Atlas, Morocco). Ichnos 13:69–79.
Brainerd, E.L., Baier, D.B., Gatesy, S.M., Hedrick, T.L., Metzger, K.A., Gilbert, S.L., and Crisco, J.J. 2010. X-ray reconstruction of moving morphology (XROMM): precision, accuracy and applications in comparative biomechanics research. Journal of Experimental Zoology, 313A:262–279.
Charbonneau, P., Hare, L., and Carignan, R. 1997. Use of X-ray images and a contrasting agent to study the behavior of animals in soft sediments. Limnology and Oceanography, 42:1823–1828.
Falkingham, P.L. 2012. Acquisition of high resolution 3D models using free, open-source, photogrammetric software. Palaeontologia Electronica, 15(1):15p.
Falkingham, P.L., Margetts, L., Smith, I.M., and Manning, P.L. 2009. Reinterpretation of palmate and semi-palmate (webbed) fossil tracks; insights from finite element modeling. Palaeogeography, Paleoclimatology, Palaeoecology, 271:69–76.
Gatesy, S.M. 2003. Direct and indirect track features: what sediment did a dinosaur touch? Ichnos, 10:91–98.
Gatesy, S.M., Baier, D.B., Jenkins, F.A. Jr., and Dial, K.P. 2010. Scientific rotoscoping: a morphology-based method of 3-D motion analysis and visualization. Journal of Experimental Zoology, 313A:244–261.
Gatesy, S.M., Middleton, K.M., Jenkins, F.A., Jr., and Shubin, N.H. 1999. Three dimensional preservation of foot movements in Triassic theropod dinosaurs. Nature, 399:141–144.
Gidmark, N.J., Strother, J.A., Horton, J.M, Summers, A.P., and Brainerd, E.L. 2011. Locomotory transition from water to sand and its effects on undulatory kinematics in sand lances (Ammodytidae). Journal of Experimental Biology, 214:657–664.
Gingras, M.K., Pemberton, S.G., Dashtgard, S., and Dafoe, L. 2008. How fast do marine invertebrates burrow? Palaeogeography, Palaeoclimatology, Palaeoecology, 270:280–286.
Hedrick, T.L. 2008. Software techniques for two- and three-dimensional kinematic measurements of biological and biomimetic systems. Bioinspiration & Biomimetics, 3:6p.
Hitchcock, E. 1858. Ichnology of New England: a report on the sandstone of the Connecticut Valley, especially its fossil footmarks, made to the government of the Commonwealth of Massachusetts, W. White, 220 p.
Howard, J.D. 1968. X-ray radiography for examination of burrowing in sediments by marine invertebrate organisms. Sedimentology, 11:249–258.
Huerta, P., Torcida Fernández-Baldor, F., Farlow, J.O., and Montero, D. 2012. Exceptional preservation processes of 3D dinosaur footprint casts in Costalomo (Lower Cretaceous, Cameros Basin, Spain). Terra Nova 00:1–6.
Ishigaki, S. 2010. Theropod trampled bedding plane with laboring trackways from the Upper Cretaceous Abdrant Nuru fossil site, Mongolia. Hayashibara Museum of Natural Sciences Research Bulletin 3:133–141.
Jackson, S.J., Whyte, M.A., and Romano, M. 2009. Laboratory-controlled simulations of dinosaur footprints in sand: a key to understanding vertebrate track formation and preservation. Palaios, 24:222–238.
Jackson, S.J., Whyte, M.A., and Romano, M. 2010. Range of experimental dinosaur (Hypsilophodon foxii) footprints due to variation in sand consistency: how wet was the track? Ichnos, 17:197–214.
Jenkins, F.A., Jr., Shubin, N.H., Amaral, W.W., Gatesy, S.M., Schaff, C.R., Clemmensen, L.B., Downs, W.R., Davidson, A.R., Bonde, N., and Osbaeck, F. 1994. Late Triassic continental vertebrates and depositional environments of the Fleming Fjord Formation, Jameson Land, East Greenland. Meddelelser om Grønland, Geoscience, 32:1–25.
Maladen, R.D., Ding, Y., Li, C., and Goldman, D.I. 2009. Undulatory swimming in sand: subsurface locomotion of the sandfish lizard. Science, 325:314–318.
Maladen, R.D., Ding, Y., Umbanhowar, P.B., Kamor, A., and Goldman, D.I. 2011. Mechanical models of sandfish locomotion reaveal principles of high performance subsurface sand-swimming. Journal of the Royal Society Interface, 8:1332–1345.
Manning, P.L. 2004. A new approach to the analysis and interpretation of tracks: examples from the dinosauria. The Application of Ichnology to Paleoenvironmental and Stratigraphic Analysis. Geological Scoiety of London Special Publications, 228:93–123.
Matthews, N.A., Noble, T.A., and Breithaupt, B.H. 2006. The application of photogrammetry, remote sensing and geographic information systems (GIS) to fossil resource management. Bulletin New Mexico Museum of Natural History and Science, 34:119–131.
Milàn, J. and Bromley, R.G. 2006. True tracks, undertracks and eroded tracks, experimental work with tetrapod tracks in laboratory and field. Palaeogeography, Palaeoclimatology, Palaeoecology, 231:253–264.
Milàn, J. and Bromely, R.G. 2008. The impact of sediment consistency on track and undertrack morphology: experiments with emu tracks in layered cement. Ichnos, 15:19–27.
Miranda, D.L., Schwartz, J.B., Loomis, A.C., Brainerd, E.L., Fleming, B.C., and Crisco, J.J. 2011. Static and dynamic error of a biplanar videoradiography system using marker-based and markerless tracking techniques. Journal of Biomechanical Engineering, 133:8p.
Olsen, P.E. 2002. Field guide for non-marine boundary events in the Newark Basin (New Jersey, Pennsylvania, and Connecticut), Eastern United States and their litho-, chrono- and biostratigraphic context. Guidebooks for Field Workshops of the International Geological Correlation Programme, 458:181p.
Padian, K.P. 2003. Pterosaur stance and gait and the interpretation of trackways. Ichnos, 10:115–126.
Pérez-Lorente, F. and Herrero Gascón, J. 2007. El movimiento de un dinosaurio deducido de una rastrillada terópoda con estructuras de inmersión de los pies en barro y de arrastre de cola (Formación Villar Del Arzobispo. Galve, Teruel, España). Revista Española de Paleontología 22:157–174.
Rainforth, E.C. 2005. Ichnotaxonomy of the fossil footprints of the Connecticut Valley (Early Jurassic, Newark Supergroup, Connecticut and Massachusetts). PhD dissertation, Columbia University, 1302p.
Romero-Molina, M.M., Sargeant, W.A.S., Pérez-Lorente, F., López, A., and Requeta, E. 2003. Orientation and characteristics of theropod trackways from the Las Losas palaeoichnological site. Ichnos 10:241–254.
Söderkvist, R. and Wedin, P. 1993. Determining the movements of the skeleton using well-configured markers. Journal of Biomechanics, 26:1473–1477.
Thulborn, R.A. 1990. Dinosaur Tracks. London: Chapman & Hall.
