Visualizing the fluid flow through the complex skeletonized respiratory structures of a blastoid echinoderm
Article number: 18.1.14A
https://doi.org/10.26879/492
Copyright Paleontological Society, March 2015
Author biographies
Plain-language and multi-lingual abstracts
PDF version
Submission: 13 May 2014. Acceptance: 8 February 2014
{flike id=1078}
ABSTRACT
Spiraculate blastoids have extraordinary internal skeletonized respiratory structures, the hydrospires. However, the detailed pattern of seawater flow within them is unknown, making it difficult to assess their respiratory effectiveness. Using a scaled-up (72x) 3D printed physical model to visualize the flow of water through the most distal (aboral) part of the hydrospire of Pentremites rusticus, we show that flow was consistent with effective respiratory exchange in the hydrospire folds - the flow continued horizontally within the hydrospire folds after passing through the hydrospire pore canals and only developed an adoral component to its velocity once it had entered the hydrospire canals. The observed orderly laminar flow is consistent with the Reynolds numbers we estimate for a living blastoid (Re = 0.0008-0.05). While most functional analyses of spiraculate hydrospires focus on their respiratory function, it is also possible that they played a role in feeding, helping to draw water past the brachioles, which is a hypothesis that is amenable to future testing.
Tony L. Huynh. Department of Integrative Biology, University of California, Berkeley, Berkeley, California 94720-3140 USA. huynhtony@berkeley.edu
Dennis Evangelista. Department of Biology, University of North Carolina at Chapel Hill, Chapel Hill, North Carolina 27599-3280 USA. devangel@live.unc.edu
Charles R. Marshall. University of California Museum of Paleontology and Department of Integrative Biology University of California, Berkeley, Berkeley, California, 94720-4780 USA. crmarshall@berkeley.edu *Author for correspondence
Keywords: Blastoidea; Echinodermata; Functional morphology; Fluid flow; Hydrospire; Three dimensional printed model
Huynh, Tony L., Evangelista, Dennis, and Marshall, Charles R. 2015. Visualizing the fluid flow through the complex skeletonized respiratory structures of a blastoid echinoderm. Palaeontologia Electronica 18.1.14A: 1-17. https://doi.org/10.26879/492
palaeo-electronica.org/content/2015/1073-blastoid-hydrospire-fluid-flow
INTRODUCTION
Spiraculate blastoids are a polyphyletic group of beautiful (Haeckel, 1904) stalked echinoderms found in Ordovician through Permian rocks (Beaver et al., 1967; Clarkson, 2009), with feeding appendages (the brachioles) attached to the ambulacra, which in turn formed part of their calyx (Sprinkle, 1973). Here we examine the function of their most notable feature, the extraordinary internal skeletonized respiratory structures, the hydrospires (Macurda, 1965, 1980; Beaver et al., 1967; Sprinkle, 1973; Katz and Sprinkle, 1976; Beaver, 1996; Schmidtling and Marshall, 2010).
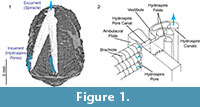
Functional analysis of the skeletonized respiratory structures of non-blastoid blastozoans (e.g., Paul, 1972; Paul and Bockelie, 1983) has been aided by the fact that these simpler structures consisted of straight, constant diameter, tubes or channels with no branching, so there is no ambiguity in how water flowed through them. This made it possible for Paul (1972), for example, to compute the relative effectiveness of five basic types of non-blastoid respiratory pore-structures he identified at that time. In contrast, the hydrospires of the spiraculate blastoids (Figure 1.1) exhibit changes in diameter, branching, anastomosis, and a geometrically complex system of pores and folds making it difficult to infer from visual inspection exactly how water flowed within them. However, it is generally agreed (Beaver et al., 1967) that seawater was taken into the hydrospires via the large number of hydrospire pores running down the edges of the ambulacra, passed through the connecting pore canals into a vestibule, and thence into one of several sub-parallel folds, each of which terminates in a canal (Figure 1.2). The folds and canals run most of the length of the ambulacra and unite at, or close to, the excurrent orifice, the spiracle (Figure 1.1). In some taxa, for example, Pentremites rusticus analyzed here, the hydrospires are paired, each pair sharing a single excurrent spiracle.
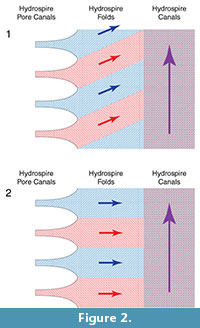
To help determine whether the narrow folds served as oxygen exchange surfaces, we need to know how water flowed over them. One possibility (Hypothesis 1) is that the water flow in the hydrospire folds had an adoral component to it (Figure 2.1). Such a flow component represents respiratory leakage: as water flows adorally, successively more of the water passing through the folds is “spent”; as it passed over more adoral portions of the folds, it would already have been stripped of oxygen. Alternatively, it would seem more effective if new, oxygen-rich, water taken in through the pores did not mix with previously spent water, i.e., if the water flowed horizontally through the folds, only developing an adoral component to its velocity once it had entered the canals (Hypothesis 2) (Figure 2.2). This second hypothesis was suggested by Schmidtling and Marshall (2010), and implies that the hydrospire canals functioned exclusively as excurrent conduits. Hypothesis 1 implies a less effective hydrospire than Hypothesis 2, but the hydrospires have a large surface area, which may have been able to compensate for a low effectiveness, in the same way that some non-blastoid blastozoans with less effective respiratory pore-structures appear to have compensated for this fact by having a large number of the structures (Paul, 1972). Hypothesis 2 suggests a more effective oxygen exchange, with the large surface area of the hydrospires either enabling high oxygen use, and/or, allowing enhanced survival with low oxygen availability.
EXPERIMENTAL APPROACH
Given that visual inspection of the fossil morphology does not provide a direct way to test between Hypotheses 1 and 2, and the lack of close living relatives or analogues for the blastoids, we applied another approach for probing the details of hydrospire function, through use of principles and techniques from engineering fluid mechanics. As an example of this approach, the principle of continuity establishes that in systems without leaks, what goes in must come out (reviewed in Kundu and Cohen, 2004). Thus, in piping systems with changing diameters it can be used to infer overall flow speeds, for example, in vertebrate circulatory systems and in marine invertebrates respiratory and feeding structures (reviewed in LaBarbera, 1990; Vogel, 1994). For a system with constant volume flow rate, the flow speed and cross sectional area perpendicular to the flow direction are inversely proportional, as might be seen in blood vessels and capillaries, or in the feeding apparatus of sponges.
In the context of blastoids, Schmidtling and Marshall (2010) used serial sectioning of Pentremites rusticus and the principle of continuity to examine flow along the length of the hydrospire. They found that the hydrospire canals widened as flow moved adorally, at a rate that kept pace with additional water taken in through the progressively more adoral incurrent hydrospire pores. This would have maintained flow within the hydrospire canals at a constant speed (Schmidtling and Marshall, 2010). But with a complex internal anatomy, use of the principle of continuity has its limitations. For example, Schmidtling and Marshall (2010) assumed that there was no adoral flow within the folds, so that the area of hydrospire folds need not be considered. However, if there was an adoral component to the flow within the folds, then Schmidtling and Marshall’s (2010) measurements are inappropriate - under Hypothesis 1 (Figure 2.1) the flow in the folds represents a leak with respect to the flow in the canals. Thus, while the principle of continuity provides clues as to the overall flow into and out of the animal, further tests of respiratory effectiveness, to decide between Hypotheses 1 and 2, requires a more detailed knowledge of the flow, specifically, the local patterns of velocity within the folds.
Thus, we had to find a more powerful way of determining the flow within the hydrospires. The approach we used was direct flow visualization (Smits and Lim, 2003) in a geometrically similar physical model.
METHODS AND MATERIALS
The limits in resolution of the 3D printers available for making geometrically similar physical models coupled with the small size of the hydrospires meant that we needed to make an enlarged model of the hydrospires. The scale factor used was 72 times real size (see below), to ensure that the internal plumbing was intact in the model so that we could run water through it. However, this scale put limits on how much of the hydrospire could be printed (see below). Thus, we performed flow visualization in a 72x scale model of just the distal (aboral) portion of a hydrospire, encompassing the first (most aboral) 10 hydrospire pores. While other quantitative methods exist, e.g., particle image velocimetry (PIV), dye visualization was sufficient for answering our research questions, as well as being inexpensive and easy to use.
Reynolds Number and Flow Regime for Living Pentremites rusticus
To conduct meaningful flow visualization, we needed to establish that the model would be in the same flow regime as the actual organism. A parameter which establishes this equivalence is the Reynolds number (Re), a dimensionless number that reflects the relative importance of inertial versus viscous forces in fluid flow (Vogel, 1994; Blevins, 2003; Kundu and Cohen, 2004):
Re = U Dh/ν (1)
where U is the flow velocity, Dh is the hydraulic diameter of the space the fluid flows through, and ν is the kinematic viscosity (Vogel, 1994).
Similar Re numbers translate into similar flow conditions, and thus models are typically tested at or near the Reynolds number of the original organism (reviewed in Vogel, 1994). Using scaled-up models provides a convenient platform from which to conduct flow studies, especially where the size of organisms or their organs are inconveniently small (Chamberlain, 1969, 1976; LaBarbera, 1990; Santhanakrishnan et al., 2009; Munk, 2011; Waldrop, 2012; Zeng, 2013), as is the case with blastoid hydrospires. While under certain conditions it is critical to match the Reynolds number (e.g., when examining creeping flow for external flow around appendages ([Koehl and Strickler, 1981; Koehl, 2001; Waldrop, 2013), or when examining transitional Reynolds numbers in the range 100 to 500 in external flows [Munk, 2011]), under other conditions the relevant fluid mechanics are partially scale-independent. For example, in internal, ciliary-driven, steady, non-pulsatile flow in pipes and between parallel plates, as is the case here, flows below Re~2000 are laminar (Avallone and Baumeister, 1996; Blevins, 2003; Kundu and Cohen, 2004). However, for internal flows with Re numbers in the range of 10 to 1000, it is possible for the fluid to remain laminar while experiencing regions of recirculation around cavities or discontinuities in geometry, which complicates inferences of the exact path of fluid flow. In computational fluid dynamic (CFD) simulations and physical model tests of embryonic zebrafish hearts, tests below Re = 10 were found not to exhibit these complications, even when minor geometric discontinuities were present (Santhanakrishnan et al., 2009). Thus, at low Re < 1, and perhaps as high as Re = 10, such patterns are expected to be absent. In this regime, viscosity dominates the flow, and it is difficult to cause any mixing within the flow (Vogel, 1994).
So, what was the Re of fluid flow inside the hydrospires of a living blastoid (specifically, within the folds, where respiratory exchange is presumed to have occurred)? To compute the Reynolds number we required an estimate of the flow velocity, the hydraulic diameter of the folds, and the kinematic viscosity (see equation [1]).
Paul (1978), using data from living echinoderms, estimated ciliary driven flow velocities in non-blastoid blastozoans of 0.6 x 10-3 m/s, the value we used here. However, cilia are not preserved in fossil echinoderms, so we don't know where they were situated within the hydrospires. If they were located in the hydrospire folds, the estimated flow velocity in the folds is simply 0.6 x 10-3 m/s. However, if the cilia were in the pore canals, which is perhaps less likely given that they may have choked the canals (C.R.C. Paul, personal commun., 2012), the flow velocity in the folds would have been lower due to the larger cross sectional area of the folds compared with the pore canals (Figure 1.2). This velocity can be estimated. According to the principle of continuity:
Apore Upore = Afolds Ufold (2)
where A and U designate the cross sectional areas and water velocities respectively. The pores were circular and had an average diameter (d) of 25.4 mm (over the first eight pores), and in the hydrospire we modeled each pore was connected to three folds, each with rectangular cross sectional area normal to the orientation of the pore canals (A folds) of 265 x 43 (h x w) mm 2 (the pore spacing and therefore the height of the folds between adjacent pores was 260-270 mm, or 7-10 times the pore diameter; Schmidtling and Marshall, 2010). Applying continuity, we can estimate the velocity in the folds:
π(d/2)2Ucilia = 3 h w Ufold (3)
Thus, the area available for flow to expand into in the folds was 67 times the area of the pore, thus the velocity in the folds would have decreased 67 times, from 0.6 x 10-3 m/s in the pore canal to 0.09 x 10-4 m/s in the folds.
With these two estimates of the velocity in the folds, calculation of the Re proceeded. For fluid flow between two parallel plates, the hydraulic diameter is approximately twice the distance between the plates (Fox et al., 2004), thus Dh = 85 mm. The kinematic viscosity for seawater (at a salinity of 35 psu) ranges from 1.834 x 10-6 m 2 /s at 0°C to 0.944 x 10-6 m 2 /s at 25°C (Lide, 2006). The highest estimated Re number is if the cilia were in the folds, in relatively warm seawater, at 25°C (Re = 0.051). The lowest estimate was if the cilia were in the pore canals, in cold water (Re = 0.0004). Both estimates are much less than Re = 1. Thus, the water flow within the hydrospires was in a regime where flow is laminar and recirculation and mixing should be absent. Table 1 presents the data used in the calculations; full calculations are in Supplementary Material, Table S1, Table S2, and Table S3.
Construction of the Physical Model
Schmidtling and Marshall (2010) used destructive serial sectioning to examine the 3D hydrospire structure of one of three specimens of Pentremites rusticus (Hambach, 1903) purchased at the Tucson Gem and Mineral Show (the other two specimens can be found in UCMP [UCMP 123100, UCMP 123101]) - this provided the basic 3D structure for modeling. Unfortunately, the original raw image files created some 20 years ago are lost (pointing to the importance of proper archiving of digital resources). However, these images had too low a resolution to print a 3D model directly: the original images provided 20 μm resolution for 75% of the calyx, 40 μm resolution for 10% of the calyx, and 200 μm resolution for 15% of the calyx, and thus were unable to resolve the narrowest parts of the hydrospire system, the smallest pore canals leading into the hydrospire (24 μm diameter). Thus, we used Figure 3 from Schmidtling and Marshall (2010) to make a digital model (Figure 3.1) to serve as the template for the 3D printer.
The digital model of the distal end of the hydrospire (UCMP 123102) was developed in a freely available 3D solid modeling program (Blender 2.69, The Blender Foundation, Amsterdam, Netherlands; www.blender.org) (Figure 3). The supplementary stereo lithography [STL] file is available for download in a zipped file with all the supplemental material. Blender was used for ease in modeling curved biological shapes (Munk, 2011; Evangelista, 2013; Zeng, 2013; Evangelista et al., 2014).
The narrowest passages within the respiratory system are the most distal (aboral) hydrospire canals, 25.9 mm in diameter averaged over the 10 most aboral pores (Schmidtling and Marshall, 2010). We estimated that these would need to be scaled up to about 1 to 2 mm in diameter to ensure that water would run through the model; limitations of the 3D printer meant that holes below this size might not be complete in the final print. Thus, the model was printed at a scale factor of ~72x (72 x 25.9 μm = ~1.86 mm for the diameter of the printed pores). This scale factor meant that only part of the hydrospire could be printed, and thus the model was restricted to approximately the first (aboral) quarter of the hydrospire. The scale model was printed on a 3D printer (ProJet HD3000, 3D Systems, Rock Hill, SC) using a translucent ABS polymer (Figure 3.2). Use of a scaled up model permitted easy visualization of the fluid flow through the hydrospires, something that would have proven difficult if we printed a 1:1 scale model.
Following removal of the support wax from the 3D print, a viewing window was milled down the entire height of the model to a high surface finish using an end mill, then polished further by hand, to provide clear viewing of flow within the folds. The overall dimensions of the final model were 17.0 x 8.7 x 6.9 cm (h x l x w), with a pore diameter of ~1.86 mm, a spacing between the pores of 15.3 mm, and a distance between the walls of the hydrospire folds an average of 3.1 mm.
Test Conditions and Flow Visualization Using Dye
To match the Re in the scale model operating in freshwater (ν = 1 x 10-6 m2/s at 25°C) would have required a pore velocity of 0.6 x 10-3 m/s, which would have been prohibitively small; testing in mineral oil ( ν = 30 x 10-6 m2/s) would have permitted a pore velocity of 18 x 10-3 m/s but was cost-prohibitive. We opted instead to test with fresh water at higher speed (pore velocity 3.2 x 10-3 m/s; fold velocity of 61 x 10-6 m/s), or Re ~0.376, about seven times the largest estimated Re for blastoids in life, but still within the range for which the steady, fully-developed internal flow in a pipe is in the laminar regime, that is at Re <1 (full calculations in Supplementary Material, Table S1). Thus, if laminar flow is observed in the scaled-up model, i.e., if no mixing is seen, then it can be assumed that it was also laminar in living Pentremites rusticus .
The completed model was placed in a 10-gallon aquarium and connected to an inlet header (Figure 3.2) made of standard Tygon R-3603 PVC laboratory tubing (inside diameter 1/8-inch [3.175 mm]). Flow was driven by a laboratory faucet throttled to provide very low flow. Total volumetric flow rate (6.9 x 10-8 m3/s) was measured directly by observing the rate of level change in the tank (Supplementary Material, Table S1, Table S2, and Table S3). To determine whether there was mixing of water in the folds, and whether or not there was an adoral flow component within the hydrospires, we injected 20 ml of red or blue water-soluble food coloring (Safeway, Pleasanton, CA) into each of two inlet header tubes that lay down stream of the primary header tube. Inlet header tubes were arranged so that the water flowing into adjacent pores was of different color (Figure 4). The tubing was connected to the model via standard 1 ml pipette tips, which had their tapered ends inserted into the hydrospires pores (Figure 3.2).
The resulting flow was filmed through the polished window in the model using a Nikon D300S DSLR (Nikon Inc., Tokyo, Japan), operated in high definition (HD) mode at 30 fps. Video was taken over the entire 24-minute course of the experiment to capture steady-state flow.
RESULTS
Figure 4 shows a still image of the flow pattern nine minutes into the experiment. The flow maintained horizontal bands of distinct color through out the course of the experiment, matching the flow pattern expected under Hypothesis 2 (Figure 2.2). A movie of one of the experimental runs (sped up 16 times) is available in the online Supplementary Material.
DISCUSSION
Study Limitations
In Table 1 we provide relatively precise estimates of the Re of the fluid flow through the hydrospire folds of a blastoid hydrospire. Nonetheless, the estimates vary by approximately two orders of magnitude (from 0.0004 to 0.05). Most of this variation, 50-fold, stems from our uncertainty in the location of the cilia that drove seawater flow in the hydrospires. The other source of variation stems from the approximately two-fold difference in the kinematic viscosity of seawater from 0°C to 25°C. We do not know how to determine where the cilia were distributed within the hydrospires. On the other hand, the fossil locality provides some clue regarding water temperature - the specimen modeled was found in Oklahoma in the Morrowan (Schmidtling and Marshall, 2010), which was equatorial in the Lower Pennsylvanian (the Morrowan is approximately equivalent to the Bashkirian). While we have no secure estimates of the seawater temperature at the time, it appears the Earth’s climatic system was broadly similar to that of today, with evidence of polar ice at the time and roughly comparable CO2 levels (Fielding et al., 2008). Thus, the equatorial ocean temperature of the shallow marine was probably much closer to 25°C than 0°C at the time, and so the Re was probably between 0.0008 and 0.05.
There are several other sources of uncertainty - for example we do not know the velocity at which the cilia drove the seawater flow, although it seems unlikely that we are in error by more than a factor of two. We also don’t know how much of the volume was occupied by the cilia, nor do we know the thickness of the epithelium that lined the hydrospires. If the epithelium occupied 10% the space between the hydrospire folds, the Re would increase by a factor of ~2. Further, the estimates provided in Table 1 are based on just one specimen of one species (Pentremites rusticus). One would expect different Re numbers in different individuals, at different ontogenetic stages (Waldrop, 2013; see also Dexter et al., 2009 for an analysis of the relationship between hydrospire allometry and respiration), and certainly between different species. Moreover, even within an individual, there is variation within a given hydrospire, with changes in the diameter of the hydrospire pores and the number of folds (from three to five then back to four) as one moves adorally, as well as between hydrospires, particularly between the anal and the four non-anal hydrospires (Beaver et al., 1967; Schmidtling and Marshall, 2010).
It is difficult to quantify all of these uncertainties, but as discussed above, orderly laminar flow is found when Re < 1 (Santhanakrishnan et al., 2009), and only when Re > 10 is recirculation at channel discontinuities sometimes found. Consistent with these results, in our physical model, orderly laminar flow was observed at Re = 0.4. Thus, it would seem that even our highest estimates of the Re in the living blastoid are at least 20-fold and probably 200-fold lower than the Re where orderly laminar flow might start to break down.
Flow and Physiology
With the study limitations in mind, our results support Hypothesis 2 - Figure 4 shows that water does not mix within the hydrospire fold portion of the hydrospire structure in the scaled-up physical model. There are clear horizontal flow-bands within the folds themselves, indicating the lack of a vertical (adoral) component to flow within the hydrospire folds. Incurrent water flows into the structure at the hydrospire pores and remains in horizontal bands until it reaches the excurrent canals. Water from a specific pore (red) only mixes with water from adjacent pores (blue) after it reaches the excurrent canal (shown in purple in Figure 2); in the canal, the mixed water flows vertically/adorally towards the excurrent spiracle. Since testing at higher Re overestimates the amount of mixing, we feel justified in extrapolating results down to lower Re in the once-living blastoid.
The observed pattern supports the predictions of (Schmidtling and Marshall, 2010) and Hypothesis 2 (Figure 2). The significance of this flow pattern is that the hydrospires in Pentremites potentially represent an effective gas exchange surface in which all the fold surface area is provided with “fresh” flow from the hydrospires pores distributed along much of the length of the animal, while the hydrospire canals would primarily have functioned as excurrent conduits.
We note that the specific flow pattern observed does require any control on behalf of the blastoid, apart from propelling the water flow; had we observed some other flow pattern, we would have been faced with the possibility that the distribution of cilia within the hydrospires might have been used to direct the water flow in a different path than observed. We cannot see how one would determine if cilia were used to divert fluid flow from the “cilia-free” path.
Relative Efficiency of the Spiraculate Blastoid and Non-Blastoid Blastozoan Respiration
Many Paleozoic echinoderms, particularly from the lower Paleozoic, had remarkable skeletonized respiratory structures (Ubaghs, 1975). Paul (1968, 1972, 1978) and Paul and Bockelie (1983) in their classic functional studies of non-blastoid blastozoan respiration, have shown for the taxa that they studied that between 25% and 75% of their thecal surface area was devoted to specialized respiratory structures. Paul (1972) also showed that exothecal respiratory structures (those where the oxygen exchange surfaces lay outside the calyx) had about half the efficiency (defined as the respiratory rate achievable per unit length) compared with endothecal respiratory structures (where oxygen exchange is inferred to have occurred within the calyx), in part because exothecal structures could not take advantage of the coelomic counter currents needed to maximize extraction of oxygen from the water that flowed through the structures.
For the spiraculate blastoids, the respiratory structures (the internal hydrospires) were bathed in coelomic fluid, and it seems likely that cilia were present that enabled the coelomic fluid to flow past the hydrospire folds counter to the direction of the water flow within the hydrospires, thus maximizing the extraction of oxygen.
The hydrospires of Pentremites rusticus are especially well developed, and we wondered how large its respiratory surface area was compared with the surface area of its calyx. To make this estimate we used the data from Schmidtling and Marshall (2010). The total respiratory surface area = the average hydrospire fold length (~0.1 the diameter of the calyx; 1 mm), multiplied by the average number of folds per hydrospire (~4.3), multiplied by 2 sides per fold, multiplied by the number of hydrospires (10), multiplied by the total length of hydrospire folds within the calyx (~10.9 mm). This yields a total surface area of ~937 mm2. The specimen was 21 mm tall, with a maximum diameter of 10 mm, and thus had an external surface area of ~560 mm2 (ignoring the area of the spiracles and the attachment of the stalk, and the fact that the calyx is not exactly an ellipsoid). Thus, the respiratory surface area is ~168% the total external surface area.
The first-order calculation made above indicates that the blastoid Pentremites rusticus had a larger relative respiratory exchange area than the non-blastoid blastozoans studied by Paul (1972), by a factor of two to seven. Given that the non-blastoid blastozoans with the larger relative respiratory surface areas studied by Paul (1972) were unable to make use of coelomic counter currents to aid in respiration, the realized respiratory capacity of the blastoid examined here was probably toward the upper end of this range if blastoids employed coelomic counter currents. It would be interesting to compute the relative respiratory surface areas for taxa that have been described since Paul’s (1972) study, for example, the impressive glyptocystitid rhombiferan Hadrocystis pauli (Sprinkle, 1974), as well as Late Ordovician hemicosmitoids, Ordovician parablastoids, as well as non-blastozoans, for example mitrates and the crinoids that evolved endothecal respiration. Furthermore, we know virtually nothing about the respiratory functional morphology of the open hydrospires of the fissiculate blastoids, a group that was more diverse, longer-lived, and geographically wider spread than the spiraculate blastoids, or for that matter other spiraculate blastoids.
A Relationship Between Spiraculate Hydrospire Organization and Feeding?
It is tempting to conclude that this impressive respiratory capacity was at least partially responsible for the evolutionary success of the spiraculate blastoids. However, selection can gain purchase on subtle differences in functional capacity, and so while a large respiratory capacity might have played a role in their evolutionary success, there are many other possibilities (and it is important to recognize that we selected Pentremites rusticus in part because of its unusually well developed hydrospires - most other spiraculate blastoids did not have as many hydrospire folds as exhibited by this species). For example, it is possible that the organization of the hydrospires in the spiraculate blastoids might have aided in feeding - the incurrent hydrospire pores lay at the base of the feeding brachioles, and if the cilia were located in the folds, they would have generated current velocities of 4 cm s-1 at the base of the brachioles (67 x the cilial flow velocity of 0.6 mm s-1 in the folds [see above]). As is always the case in paleontology, and even in neontological studies, it is very difficult to determine the balance of selective versus stochastic reasons for long-term evolutionary access, and when selection is implicated (for example, when it acts on only parts of the realized morphospace, which does not appear to be the case in blastoids [Foote, 1991]), it difficult to determine which selective factors were decisive. Nonetheless, further functional work, for example, testing whether the water flow into the hydrospires pores aided in feeding, or the extent to which the spiraculate blastoids were able to take advantage of feeding currents to aid the flow of water through the hydrospires, could be tested with physical models.
ACKNOWLEDGMENTS
We thank the Berkeley Center for Integrative Biomechanics Education and Research (CIBER), especially T. Libby, for use of their 3D printer, warming oven, and sonicator, D. Erwin for providing access to the UCMP facilities needed for shaping the 3D printed model, D. Lee and M. Chen (UC Berkeley Mechanical Engineering Student Machine Shop) for access to machine tools. We thank the UCMP community for feedback, advice, and assistance, especially L. Chang, J. Lim, L. Miller, T. Pincin, G. Rapacciuolo, and C. Souto. We thank A. Shabel for the invaluable use of his time, camera equipment, feedback, and photography skills. Finally we thank two anonymous reviewers for thorough and helpful reviews. This is University of California Museum of Paleontology publication number 2062.
REFERENCES
Avallone, E. and Baumeister, T. 1996. Mark's Standard Handbook for Mechanical Engineers. McGraw-Hill, New York.
Beaver, H.H. 1996. Hydrospire meshwork of the Carboniferous blastoid Pentremites Say. Journal of Paleontology, 70:333-335.
Beaver, H.H., Fay, R.O., Macurda, D.B., Moore, R.C., and Wanner, J. 1967. Blastoids, p. S297-S455. In Moore, R.C. (ed.), Treatise on Invertebrate Paleontology, Part S, Echinodermata 1, v.2. Geological Society of America and University of Kansas Press, Meriden, Connecticut, New York, New York, and Lawrence, Kansas, 1-650.
Blevins, R.D. 2003. Applied Fluid Dynamics Handbook.Krieger, Malabar, FL.
Chamberlain, J.A. 1969. Technique for scale modelling of cephalopod shells. Palaeontology , 12:48-55.
Chamberlain, J.A. 1976. Flow patterns and drag coefficients of cephalopod shells. Palaeontology, 19:539-563.
Clarkson, E.N.K. 2009. Invertebrate Palaeontology and Evolution. Wiley-Blackwell, Hoboken, New Jersey.
Dexter, T.A., Sumrall, C.D., and McKinney, M.L. 2009. Allometric strategies for increasing respiratory surface area in the Mississippian blastoid Pentremites . Lethaia, 42:127-137.
Evangelista, D.J. 2013. Aerial righting, directed aerial descent, and maneuvering in the evolution of flight in birds. Unpublished PhD Thesis, University of California, Berkeley, California, USA.
Evangelista, D., Cam, S., Huynh, T., Kwong, A., Mehrabani, H., Tse, K., and Dudley, R. 2014. Shifts in stability and control effectiveness during evolution of Paraves support aerial maneuvering hypotheses for flight origins. PeerJ, 2:e632.
Fielding, C.R., Frank, T.D., and Isbell, J.L. (eds.). 2008. Resolving the late Paleozoic ice age in time and space. Geological Society of America Special Paper, 441:1-354.
Foote, M. 1991. Morphological and taxonomic diversity in a clade's history: the blastoid record and stochastic simulations. Contributions from the Museum of Paleontology, University of Michigan, 28:101-140.
Fox, R.W., McDonald, A.T., and Pritchard, P. 2004. Introduction to Fluid Mechanics (sixth edition). John Wiley and Sons, Hoboken, New Jersey.
Haeckel, E. 1904. Kunstformen der Natur.Verlag des Bibliographlichen Instituts, Leipzig und Wien.
Hambach, G. 1903. Revision of the Blastoideae, with a proposed new classification and description of new species. Transactions of the Academy of Science of Saint Louis, 13:1-67.
Katz, S.G. and Sprinkle, J. 1976. Fossilized eggs in a Pennsylvanian blastoid. Science, 192(4244):1137-1139.
Koehl, M. 2001. Transitions in function at low Reynolds number: hair-bearing animal appendages. Mathematical Models in the Applied Sciences, 24:1523-1532.
Koehl, M. and Strickler, J.R. 1981. Copepod feeding currents: food capture at low Reynolds number. Limnology and Oceanography. 26:1062-1073.
Kundu, P. and Cohen, I. 2004. Fluid Mechanics (third edition). Academic Press, Waltham, MA.
LaBarbera, M. 1990. Principles of design of fluid transport systems in zoology. Science, 249:992-1000.
Lide, D.R. (ed.). 2006. CRC Handbook of Chemistry and Physics. Taylor and Francis, Oxford and New York City.
Macurda, D.B. 1965. Hydrodynamics of the Mississippian blastoid genus Globoblastus. Journal of Paleontology, 39:1209-1217.
Macurda, D.B. 1980. Abnormalities of the Carboniferous blastoid Pentremites . Journal of Paleontology, 54:1155-1162.
Munk, J.D. 2011. The descent of ant. Unpublished PhD Thesis, University of California, Berkeley, California, USA.
Paul, C.R.C. 1968. Morphology and function of dichoporite pore-structures in cystoids. Palaeontology, 11:697-730.
Paul, C.R.C. 1972. Morphology and function of exothecal pore-structures in cystoids. Palaeontology, 15:1-28.
Paul, C.R.C. 1978. Respiration rates in primitive (fossil) echinoderms. Thalassia Jugoslavica, 12:277-286.
Paul, C.R.C. and Bockelie, J. 1983. Evolution and functional morphology of the cystoid Spaeronites in Britain and Scandinavia. Palaeontology 26:687-734.
Santhanakrishnan, A., Nguyen, N., Cox, J., and Miller, L. 2009. Flow within models of the vertebrate embryonic heart. Journal of Theoretical Biology, 259:449-461.
Schmidtling, R.C. and Marshall, C.R. 2010. Three-dimensional structure and fluid flow through the hydrospires of the blastoid echinoderm, Pentremites rusticus . Journal of Paleontology, 84:109-117.
Smits, A.J. and Lim, T. 2003. Flow Visualization: Techniques and Examples. Imperial College Press, London.
Sprinkle, J. 1973. Morphology and Evolution of Blastozoan Echinoderms. The Museum of Comparative Zoology, Harvard University, Cambridge, Massachusetts.
Sprinkle, J. 1974. New rhombiferan cystoids from the Middle Ordovician of Nevada. Journal of Paleontology, 48:1174-1201.
Ubaghs, G. 1975. Early paleozoic echinoderms. Annual Review of Earth and Planetary Sciences, 3:1-20.
Vogel, S. 1994. Life in Moving Fluids: the Physical Biology of Flow. Princeton University Press, Princeton, New Jersey.
Waldrop, L. D. 2012. The fluid dynamics of odor capture by crabs. Unpublished PhD Thesis, University of California, Berkeley, California, USA.
Waldrop LD (2013) Ontogenetic scaling of the olfactory antennae and flicking behavior of the shore crab, Hemigrapsus oregonensis.Chemical Senses 38(6): 541-550.
Chemical Senses paper: doi: 10.1093/chemse/bjt024 Preprint [PDF, 1.4 MB]
Zeng, Y. 2013. Aerial righting, directed aerial descent, and maneuvering in stick insects. Unpublished PhD Thesis, University of California, Berkeley, California, USA.
