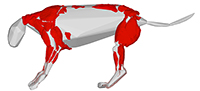
Reconstruction of the musculoskeletal system in an extinct lion
Article number: 20.2.23A
https://doi.org/10.26879/688
Copyright Palaeontological Association, May 2017
Author biographies
Plain-language and multi-lingual abstracts
PDF version
Submission: 3 June 2016. Acceptance: 1 May 2017
{flike id=1857}
ABSTRACT
Panthera atrox is an extinct lion from the Pleistocene of North America that is one of the largest felids that has ever existed. Previous reconstructions have always relied on composite specimens, and there are no known specimens that preserve soft tissues. Here we present a reconstruction of the most complete P. atrox specimen discovered to date, from which we calculate key biological parameters including body mass. Using previously published scaling equations we estimate the size of the musculature of the limbs and vertebral column. Muscles from a modern lion were scaled to the expected sizes and placed on the skeleton. The body and the limbs were digitally reconstructed (using a convex hulling method) from the skeleton before this method was repeated with the muscled limb segments. Our results from repeating this approach for a modern lion show that the combined muscle and bone convex hull reconstructions are the most accurate for reproducing the limb dimensions, including centres of mass, of large felids. From the reconstructions it is also possible to estimate the body composition of P. atrox, which allows for the most complete soft tissue reconstruction of this extinct species, including biomechanical properties of the limbs.
Andrew R. Cuff. Department of Genetics, Evolution and Environment, University College London, Darwin Building, Gower Street, London, WC1E 6BT, United Kingdom; Structure and Motion Lab, Department of Comparative Biomedical Sciences, The Royal Veterinary College, Hawkshead Lane, North Mymms, Hatfield, Herts, AL9 7TA, United Kingdom. acuff@rvc.ac.uk
Anjali Goswami. Department of Genetics, Evolution and Environment, University College London, Darwin Building, Gower Street, London, WC1E 6BT, United Kingdom. a.goswami@ucl.ac.uk
John R. Hutchinson. Structure and Motion Lab, Department of Comparative Biomedical Sciences, The Royal Veterinary College, Hawkshead Lane, North Mymms, Hatfield, Herts, AL9 7TA, United Kingdom; Department of Genetics, Evolution and Environment, University College London, Darwin Building, Gower Street, London, WC1E 6BT, United Kingdom. jhutchinson@rvc.ac.uk
Keywords: fossil reconstruction; muscles; Felidae; Panthera atrox; scaling
Final submission: Cuff, Andrew R., Goswami, Anjali, and Hutchinson, John R. 2017. Reconstruction of the musculoskeletal system in an extinct lion. Palaeontologia Electronica 20.2.23A: 1-25. https://doi.org/10.26879/688
palaeo-electronica.org/content/2017/1857-reconstructing-a-fossil-lion
INTRODUCTION
Soft tissues seldom are preserved during the fossilisation process, and, as such, most reconstructions of fossil taxa must be based, in terms of direct evidence, solely upon the skeletal remains. Those remains can be incredibly useful for reconstructing myology as the muscles often leave scars on the bone where they attach (Witmer, 1995). However, not all muscles are sufficiently large to produce muscle scars, or they may share similar or obscure attachment sites that can make them difficult to locate (Bryant and Seymour, 1990). For these ambiguous muscles, it may be possible to reconstruct soft tissues based on their presence/absence and qualitative or relative positions using the extant phylogenetic bracket (EPB) approach (Witmer, 1995). However, this method cannot calculate how large the muscles may be in the extinct species, or accurately estimate other quantifiable aspects of their anatomy. Various methods may be used to constrain muscle sizes, e.g., using the bony margins of their attachments and their pathways relative to other muscles (Hutchinson et al., 2011; Allen et al., 2013; Lautenschlager 2013; Persons IV et al., 2013; Cuff and Rayfield, 2015). However, it becomes more difficult to estimate muscle boundaries when there is no outer limit on the size of the muscles. Using convex hulls (e.g., Basu et al., 2016) or non-uniform rational b-splines (NURBs) (e.g., Bates et al., 2009) it is possible to estimate muscle volumes, but doing so incurs additional uncertainties from assumptions of the volume reconstruction methods. Thus advances in the area of soft tissue reconstruction, especially quantitative methods that can also address uncertainties, are important.
Panthera atrox (Leidy, 1853), the “American lion,” was a large felid that lived in North America during the Pleistocene epoch before going extinct at the end of the last ice age, approximately 11ka. Panthera atrox was derived from a Beringian population of P. spelaea (cave lion) evolving around 337ka (Barnett et al., 2009), with both species splitting from P. leo around 1.89Ma (Barnett et al., 2016). P. atrox has gained much attention over the last few decades due to the size of some of the specimens, with body mass estimates from the largest specimens ranging from 350 kg-420 kg (Sorkin, 2008), making the species one of the largest felids ever to have lived. However, due to the limited number of articulated or associated specimens, reconstructions have been based on composite specimens.
Here we outline a simple method for virtually reconstructing entire postcrania from CT scans using a well-preserved Panthera atrox specimen. Using muscle scaling equations from Cuff et al. (2016a, 2016b) for extant felids, we were able to estimate muscle and tendon masses and lengths for the individual. Digital representations of actual muscles from an Asian lion were then scaled so that the dimensions of the locomotor musculature of the limbs and vertebral column were reconstructed and could be placed in the appropriate positions as determined from dissections of living relatives via the EPB method. We also check how well our muscled restorations match the results of different convex hull methods applied to regions of the body.
METHODS
Page Museum specimen LACMP23-555 is a remarkably well-preserved skull and postcranial skeleton of Panthera atrox from the La Brea Tar Pits (Project 23-1), dating to approximately 35 ka (Fuller et al., 2014). The remains consist of a complete skull, complete limbs (minus manus and pes), girdles (although scapulae and pelvis are damaged), and a relatively complete vertebral column up to the caudal vertebrae (minus thoracic vertebrate T1, T5, T7, and T10). All of the bones were microCT scanned at The Aerospace Corporation (El Segundo, California, USA), with a GE Phoenix c/tome/x scanner (all scans 200 kV, 80 mA, voxel size = 0.24x0.24x0.24 mm). For the reconstruction, primarily the bones of the left side and axial skeleton (Appendix 1 for complete list) were segmented from the scans in Mimics 16.0 software (Materialise NV, Leuven, Belgium), to export .stl files representing each bone. In the case of multiple scans for individual bones (the skull and all long bones), multiple .stl files were exported, which were then merged in Meshlab 1.3.3 software (Visual Computing Lab, ISTI - CNR, Pisa, Italy) using the “Align” function. Where bones from the right side were used, these were mirrored to the left side in Meshlab to produce a complete left side of the skeleton.
The missing thoracic vertebrae T1, T5, and T7 were copied from the adjacent T2, T4, and T6 bones, respectively, as these were determined to be most similar in other felids (Randau et al., 2016). Vertebra number T10 is not present in the specimen, so this vertebra was replaced with the T10 of another specimen (LACMP 2458-19) of comparable size. The remainder of the bones from the left hand side (manus, pes, sternum, ribs, caudal vertebrae) were segmented from an Asian lion (Panthera leo persica) that had been scanned at the Royal Veterinary College using a Lightspeed Pro 16 CT scanner (GE Medical Systems) to obtain helical scans for the individual limbs and vertebral column (120 kV, 100 mA; resolution of 0.96x0.96x1.25 mm), and scaled isometrically from the 133 kg Asian lion to the estimated 207 kg body mass for this specimen of P. atrox (average from condylobasal length of 0.326 m (Mazák et al., 2011) and femoral length of 0.404 m - from the all-carnivoran equation (Anyonge, 1993), estimates of 195 kg and 219 kg, respectively). These methods were chosen rather than using bone circumferences as it has been noted that P. atrox has relatively robust bones for their length (Sorkin 2008), and using the felid-specific equations from Anyonge (1993) lead to estimates of maximal P. atrox masses potentially exceeding 600 kg. Recent works produce much lower maximal body mass estimates for P. atrox (Sorkin, 2008 - 420 kg; Christiansen and Harris, 2009 - 351 kg). Whilst there are issues with averaging two bivariate regressions (for an in depth discussion Smith, 2002 and references contained therein), we do not know which of the regressions is more reliable so we used the average of the two regressions as a guide. Those regressions’ estimates of 195 kg and 219 kg body mass differ by about 12%, which we viewed as plausibly close enough to warrant averaging them, given other potential sources of biological variation and methodological errors.
The finished .stl files for all of the bones were imported into Meshmixer 10.9.332 software (Autodesk, Inc.) where they were all manually aligned into a biologically plausible position based on the approximate standing posture of extant felids. The complete limbs were mirrored to create the right side and then aligned to the skeleton.
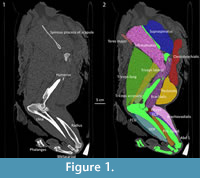The Asian lion (National Museums of Scotland specimen NMS.Z.2015.128) was CT scanned with the muscles intact, and, despite having no contrast staining with Lugol’s iodine (Kelly, 1961; Jeffery et al., 2011), we were able to segment all of the muscles from the left limbs (Figure 1). We were not able to segment the individual muscles of the vertebral column, so a gross segmentation of the cervical, thoracic, and lumbar regions of muscles was conducted. Using the scaling equations (inserting the 207 kg body mass estimate) from Cuff et al. (2016a, 2016b), the muscle belly length (i.e., length of the main striated muscle portion of the muscle-tendon unit, along its line of action) for each of the muscles was estimated for Panthera atrox. The expected muscle masses were also calculated from the Cuff et al. (2016a, 2016b) non-phylogenetic scaling equations (Appendix 2, Appendix 3, Appendix 4, Appendix 5, Appendix 6, Appendix 7, Appendix 8, Appendix 9, Appendix 10, Appendix 11, Appendix 12, and Appendix 13). The dataset from Cuff et al. (2016a, 2016b) has no large non-pantherine species and as such using the phylogenetic correction would likely reduce any real allometric signals; this could be particularly problematic due to P. atrox being a very large felid. Regardless, most muscle lengths and masses across the postcrania of felids scale (indistinguishable from) isometrically - whether or not phylogeny is accounted for - so the results are unlikely to differ greatly depending on which equation is chosen. The segmented muscles were individually scaled to match the predicted muscle length. Because the mass for each muscle and the corresponding .stl file was known from dissection of the P. leo specimen, and mass is proportional to volume (assuming density is the same for both muscles), after the length was scaled the two remaining dimensions were then scaled identically so the mass of each muscle matched that predicted from the scaling equations:
Eq 1: Mass P. atrox = Mass P. leo x length scale factor x width scale factor 2
This method was repeated for any tendons, where possible. However, the soft tissue contrast in the microCT scan images was often insufficient to separate tissues in the distal limbs, particularly for the long and relatively thin tendons. Thus most of the distal muscles lacked complete tendons in the resulting .stl files. For those distal muscles for which there were no easily segmented tendons, the tendons were recreated by extending a section of the muscle belly so that the length and mass of each tendon matched the mean lengths and masses expected from the scaling equations of Cuff et al. (2016a, 2016b). All of the scaled muscles and tendons were then placed on the left side of the P. atrox reconstructed skeleton in the appropriate positions using any evident muscle scarring patterns on the bones and the origins and insertions observed during dissections of extant species, before mirroring to the right side (as with the bones) in Meshlab.
We attempted to compare the body and segment mass estimates from convex hull models based on the reconstructions using just the skeleton and using the fully-fleshed model. This was done by using the “convex hull” filter within Meshlab for the skeletal elements from each of the body segments (e.g., Basu et al., 2016). Body mass estimates were calculated from the sum of all masses from the complete set of convex hulls using a range of densities from 893.36 kg m −3 multiplied by 1.091 to 1.322 (i.e., 974.7 kg m −3 to 1181 kg m −3 - a correction factor due to the underestimation of limb masses) (Sellers et al., 2012). In addition to total body mass estimations, convex hull estimates were made of the individual limb segments and compared to the values from the reconstructions. Finally estimations of segment masses were carried out using the same convex hull methods, but applied to the fully fleshed model for the limb segments rather than to the isolated bones. These data were validated by repeating the methods for a modern lion’s left limbs, with the total volumes for each limb segment being isolated from CT scan data, and multiplied by a density of 1060kg m -3.
RESULTS AND DISCUSSION
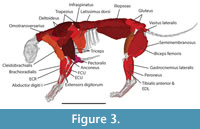
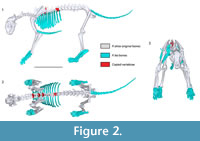Although the resulting skeletal reconstruction was, necessarily, a composite using some elements from either another Panthera atrox individuals or the cadaver of P. leo, it is the most complete scientific reconstruction of a single P. atrox specimen to date (Figure 2). Combined with the skeletal reconstruction, dissections of related species, and recent analyses of felid muscle scaling, the muscles could be reconstructed (Table 1, Table 2, and Table 3) and placed onto the skeleton (Figure 3). As somewhat of a “best case” scenario for reconstructing an extinct animal’s morphology, we used the musculature of a modern lion (phylogenetically the closest relative of P. atrox among extant felids, with less than 1.89 Ma separating them) and scaled the muscles to the predicted size using the scaling equations. These muscles, when scaled, generally matched the osteology very well (e.g., the scapular muscles of the m. infraspinatus and m. supraspinatus tightly bound by spinous process of the scapula, or the limb muscles closely wrapping the bones without intersecting each other or the bones). This good fit of the muscles to the skeleton might not be the case if the reconstructions were carried out on more distantly related taxa such as Smilodon, which is separated from all extant felids by >20 Ma. Nonetheless, this whole-body reconstruction allowed presumably improved estimates of body segment dimensions (e.g., masses, centres of mass, moments of inertia) for this individual, and could also be applied to related species in the future.
The muscle reconstructions were derived in part from body mass, so they will be sensitive to which method is used to estimate body mass. The 207 kg body mass used here was derived from equations that give mass estimates from 195-219 kg - a range of 24 kg (around 12% of body mass). Using the two estimates for body mass, the calculated estimates for muscle and tendon length differed by around 4%, and the muscle and tendon masses varied by around 12%. However, the source of greater uncertainty in the muscle and tendon estimates was the scaling equations, which for some metrics had particularly large error margins (linked to the small number of individuals sampled by Cuff et al., 2016a, 2016b). For those muscles, unrealistic predictions may occur (Appendix 2, Appendix 3, Appendix 4, Appendix 5, Appendix 6, Appendix 7, Appendix 8, Appendix 9, Appendix 10, Appendix 11, Appendix 12, and Appendix 13 for 95% confidence intervals for all muscles and tendons). Post hoc adjustments were made for those muscles by using the origin and insertion points to obtain lengths that matched the skeleton best. In particular, the m. brachioradialis muscle’s belly length was predicted to be 2.41 m long (Table 1), but from insertion and origination points was actually reconstructed at 0.275 m long, and the m. rectus femoris tendon length was predicted to be 0.65 m long, but was reconstructed as 0.060 m. This is also the case with some of the vertebral muscles (e.g., the estimated length of m. semispinalis capitis biventer was almost double the length of the entire Panthera atrox skeletal reconstruction), but the individual vertebral muscles could not be individually segmented from the CT scans.
Our method developed here for whole-body reconstruction of Panthera atrox is based on the usage of scaling equations that relate bone dimensions and body mass, permitting estimation of the latter. These equations have been shown to be very good (r2 > 0.95) at estimating body masses for extant Panthera species (Anyonge, 1993; Mazák et al., 2011) and by using them we also produced a reasonable estimation for body composition (Table 4) compared to modern P. leo. The musculature of extant lions accounts for (on average) 57.1% of total body mass, then the remainder of body mass is 11.5% skin, 12.4% skeleton, 11.8% organs, about 4.6% blood and waste, and 2.7% fat (Davis, 1962). For P. atrox, the muscles and their respective tendons reconstructed from the scaling equations of Cuff et al. (2016a, 2016b) correspond to 84.4 kg in mass (40.8% of total body mass calculated from the bone regression). Of course, other muscles (e.g., abdominal, intercostal, hyomandibular, and various intrinsic muscles of the manus, pes, and skull) would add to the muscle mass further. However, it would be surprising if there was another 16.3% of body mass in this remaining musculature as this musculature only corresponds to approximately 2-3% of total mass in domestic cats (Grand, 1977). This discrepancy may be due to the different methods of preparation between Cuff et al. (2016a, 2016b), where individual muscles were dissected, and Davis (1962), which does not appear to have removed extraneous connective tissues and intermuscular adipose tissues. This suggestion is somewhat supported by the relatively low body fat content of lions (2.7%) estimated by Davis (1962), relative to those reported for other felid species for which data are available (domestic cat: 20.9% (Lauten et al., 2000) - 24.4% (Munday et al., 1994); Lynx spp. 15 - 16% (Pitts and Bullard, 1968)).
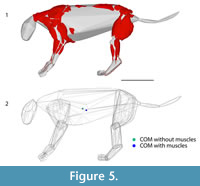
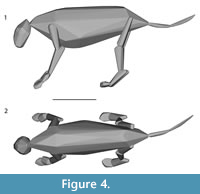Convex hull models have been used recently to reconstruct body segmental shapes and estimate body masses for skeletons with no preserved soft tissues (e.g., Sellers et al., 2012; Basu et al., 2016; Bates et al., 2016; Brassey et al., 2016). The convex hull model for the entire skeleton of P. atrox produced a volume of 0.185 m3 (Figure 4). Using the range of potential densities (Sellers et al., 2012), the body mass estimates varied from 180 kg to 219 kg. The mid-point of these two extreme ranges is 200 kg, only a few kilograms away from the ~207 kg estimate obtained from the bones, which is unsurprising as the composite bones were scaled to the 207 kg estimate. However, as convex hulls tend to underestimate total volumes, methods for estimating masses from them are heavily reliant on the density values used (e.g., a density of 1359 kg m −3 from Brassey and Sellers (2014), which they calculated to be the apparent density for convex hull models for non-primate mammals, would produce a very different estimate of 251 kg for the uncorrected convex hull of this Panthera atrox specimen). Whilst convex hull models can produce realistic estimates for total mass, they will produce regional variability, with the limb masses generally underestimated, and the core body overestimated (Sellers et al., 2012; Brassey and Sellers, 2014). The muscled reconstruction of P. atrox showed how much variability was obtained for the limb morphology (Figure 5).
On the modern lion, convex hull-based models of the bones produced segmental estimates that were up to 3.7 times and 5.23 times smaller than the masses of the muscles and bones in the proximal sections of the fore- and hindlimbs, respectively (Table 5). However, using reconstructed muscles and bones together still underestimated total limb mass by a factor of 1.3-1.8 (Table 5) due to the lack of connective tissues, blood vessels, nerves, adipose tissue, and skin. This discrepancy could be compensated for by producing a convex hull model of the limb over the muscled reconstructions, which produced mass estimates that were within 8% of the actual fleshed limb segments (Table 5), rather than producing the original ~30-80% underestimates.
For any biomechanical model of a species it is important to understand more than just the masses of the segments, but also the segmental centres of mass and moments of inertia, all of which determine how the segments might have moved (Allen et al., 2009, 2013). The convex hull models of the muscled limb segments for Panthera leo produced centre of mass (COM) estimates that were very close to those from CT scan segmentation in terms of absolute distances, and percentages of segment length (Table 6), suggesting this method of reconstructing limb segments is comparable to the original fleshed limb.
From our reconstructions of the limb segments for Panthera atrox, the mass estimates from the convex hulls over the bones relative to the muscle and bone masses are comparable to those of P. leo (Table 5 and Table 7). This result supports the conclusion that the convex hulls over the reconstructed muscles will also be similarly accurate for P. atrox as they were for P. leo. For the hindlimbs, the percentage of the total mass for each segment was very similar to those of domestic cats, but the forelimb segments in P. atrox were almost double the typical mass measured in domestic cats (Grand, 1977). As the muscle masses appear to scale isometrically in the forelimbs of felids (Cuff et al., 2016a) and there is only a few percentage points difference (in terms of total body mass) between the forelimb muscles of P. atrox and domestic cats, this increase in mass is probably linked to an increase in robustness of the bones (Sorkin, 2008; Doube et al., 2009) and may be correlated with the importance of the forelimbs to tackle prey in larger felids (Meachen-Samuels and Van Valkenburgh, 2009). Considering the close concordance of centres of mass between the segmental convex hull reconstructions of P. leo and its CT scan segmentation (Table 6), we can confidently reconstruct the limb segment COMs of P. atrox (Table 8), as well as the moments of inertia (Table 9). Additionally, we seemed to be able to more accurately estimate whole body COM, which is more posteroventrally located (5.2 cm posteriorly, 3.1 cm ventrally) in the muscled convex hull models than in models using just the skeleton (Figure 5). By using empirical data from extant lions and other felids to reconstruct the muscles (and thus body segments) quantitatively, we were better able to reconstruct this fossil taxon in detail that was previously unobtainable.
CONCLUSIONS
Our microCT scan data from one very complete skeletal specimen enabled a new reconstruction of Panthera atrox in more complete detail than before, although where there were incomplete data we had to use portions of closely related taxa, and thus our reconstruction is still a composite. Using data derived from dissections of extant felids spanning a range of body masses, it was possible to use regressions to estimate the size of the locomotor musculature of this specimen of P. atrox. These reconstructions allowed for more accurate estimates of limb masses (and the centre of masses of individual segments) from convex hull modelling than previous methods using just the bones. We supported this presumption by conducting validation tests on a modern lion’s body segments, using multiple methods. By doing the reconstructions of the skeleton, segmental inertial properties, and in combination with the musculature data, it was possible to create a full musculoskeletal reconstruction. In addition, our reconstructions of the musculature allow for body composition estimates for P. atrox for the first time. Whilst the reconstruction here was carried out mainly in freely available software (e.g., Meshlab) with licensed software used only for the CT scan segmentation, it is entirely possible to carry out future reconstructions only in open source software (e.g., SPIERS; Sutton et al., 2012), expanding the accessibility of this methodology to researchers worldwide.
ACKNOWLEDGEMENTS
This work was funded by Leverhulme Trust grant RPG 2013-124 to A. Goswami (UCL) and J.R. Hutchinson (RVC). We thank M. Randau (UCL) for preliminary assessment of the specimen, A. Farrell from The George C. Page Museum, and G. Takeuchi and L. Chiappe from the NHMLA for allowing access to this specimen and facilitating its loan for scanning, and N. Ives and G. Stupian from The Aerospace Corporation for scanning this specimen. We finally thank two anonymous reviewers for their comments that improved this paper.
REFERENCES
Allen, V., Bates, K.T., Li, Z., and Hutchinson, J.R. 2013. Linking the evolution of body shape and locomotor biomechanics in bird-line archosaurs. Nature, 497:104-107. doi:10.1038/nature12059
Allen, V., Paxton, H., and Hutchinson, J.R. 2009. Variation in center of mass estimates for extant sauropsids and its importance for reconstructing inertial properties of extinct archosaurs. The Anatomical Record, 292:1442-1461.
doi:10.1002/ar.20973
Anyonge, W. 1993. Body mass in large extant and extinct carnivores. Journal of Zoology, 231:339-350. doi:10.1111/j.1469-7998.1993.tb01922.x
Barnett,R., Mendoza, M.L.Z., Soares, A.E.R., Ho, S.Y.W., Zazula, G., Yamaguchi, N., Shapiro, B., Kirillova, I.V., Larson, G., and Gilbert, M.T.P. 2016. Mitogenomics of the extinct cave lion, Panthera spelaea (Goldfuss, 1810), resolve its position within the Panthera cats. Open Quaternary, 2.
doi:10.5334/oq.24
Barnett, R., Shapiro, B., Barnes, I., Ho, S.Y., Burger, J., Yamaguchi, N., Higham, T.F., Wheeler, H.T., Rosendahl, W., Sher, A.V., Sotnikova, M., Kuznetsova, T., Baryshnikov, G.F., Martin, L.D., Harington, C.R., Burns, J.A., and Cooper, A. 2009. Phylogeography of lions (Panthera leo ssp.) reveals three distinct taxa and a late Pleistocene reduction in genetic diversity. Molecular Ecology, 18:1668-1677.
doi:10.1111/j.1365-294X.2009.04134.x
Basu, C., Falkingham, P.L., and Hutchinson, J.R. 2016. The extinct, giant giraffid Sivatherium giganteum: skeletal reconstruction and body mass estimation. Biology Letters, 12.
doi:10.1098/rsbl.2015.0940
Bates, K.T., Mannion, P.D., Falkingham, P.L., Brusatte, S.L., Hutchinson, J.R., Otero, A., Sellers, W.I., Sullivan, C., Stevens, K.A., and Allen, V. 2016. Temporal and phylogenetic evolution of the sauropod dinosaur body plan. Royal Society Open Science, 3:150636.
Bates, K.T., Manning, P.L., Hodgetts, D., and Sellers, W.I. 2009. Estimating mass properties of dinosaurs using laser imaging and 3D computer modelling. PLoS ONE, 4:e4532. doi:10.1371/journal.pone.0004532
Brassey, C.A. and Sellers, W.I. 2014. Scaling of convex hull volume to body mass in modern primates, non-primate mammals and birds. PLoS ONE, 9:e91691. doi:10.1371/journal.pone.0091691
Brassey, C.A., O’Mahoney, T.G., Kitchener, A.C., Manning, P.L., and Sellers, W.I. 2016. Convex-hull mass estimates of the dodo (Raphus cucullatus): application of a CT-based mass estimation technique. PeerJ, 4:e1432.
Bryant, H.N. and Seymour, K.L. 1990. Observations and comments on the reliability of muscle reconstruction in fossil vertebrates. Journal of Morphology, 206:109-117. doi:10.1002/jmor.1052060111
Christiansen, P. and Harris, J. 2009. Craniomandibular morphology and phylogenetic affinities of Panthera atrox: implications for the evolution and paleobiology of the lion lineage. Journal of Vertebrate Paleontology, 29:934-945.
Cuff, A.R. and Rayfield, E.J. 2015. Retrodeformation and muscular reconstruction of ornithomimosaurian dinosaur crania. PeerJ, 3:e1093.
doi:10.7717/peerj.1093
Cuff, A.R., Sparkes, E.L., Randau, M., Pierce, S.E., Kitchener, A.C., Goswami, A., and Hutchinson, J.R. 2016a. The scaling of postcranial muscles in cats (Felidae) I: forelimb, cervical, and thoracic muscles. Journal of Anatomy.
doi:10.1111/joa.12477
Cuff, A.R., Sparkes, E.L., Randau, M., Pierce, S.E., Kitchener, A.C., Goswami, A., and Hutchinson, J.R. 2016b. The scaling of postcranial muscles in cats (Felidae) II: hindlimb and lumbosacral muscles. Journal of Anatomy.
doi:10.1111/joa.12474
Davis, D.D. 1962. Allometric relationships in lions vs. domestic cats. Evolution, 16:505-514.
Doube, M., Wiktorowicz Conroy, A., Christiansen, P., Hutchinson, J.R., and Shefelbine, S. 2009. Three-dimensional geometric analysis of felid limb bone allometry. PLoS One, 4(3):e1742.
Fuller, B.T., Fahrni, S.M., Harris, J.M., Farrell, A.B., Coltrain, J.B., Gerhart, L.M., Ward, J.K., Taylor, R.E., and Southon, J.R. 2014. Ultrafiltration for asphalt removal from bone collagen for radiocarbon dating and isotopic analysis of Pleistocene fauna at the tar pits of Rancho La Brea, Los Angeles, California. Quaternary Geochronology, 22:85-98.
doi:10.1016/j.quageo.2014.03.002
Grand, T.I. 1977. Body weight: its relation to tissue composition, segment distribution, and motor function. I. Interspecific comparisons. American Journal of Physical Anthropology, 47:211-240.
doi:10.1002/ajpa.1330470204
Hutchinson, J.R., Bates, K.T., Molnar, J., Allen, V., and Makovicky, P.J. 2011. A computational analysis of limb and body dimensions in Tyrannosaurusrex with implications for locomotion, ontogeny, and growth. PLoS ONE, 6:e26037.
doi:10.1371/journal.pone.0026037
Jeffery, N.S., Stephenson, R.S., Gallagher, J.A., Jarvis, J.C., and Cox, P.G. 2011. Micro-computed tomography with iodine staining resolves the arrangement of muscle fibres. Journal of Biomechanics, 44:189-192.
doi:10.1016/j.jbiomech.2010.08.027
Kelly, F.C. 1961. Iodine in medicine and pharmacy since its discovery-1811-1961. Proceedings of the Royal Society: Medicine, 54:831-836.
Lauten, S.D., Cox, N.R., Baker, G.H., Painter, D.J., Morrison, N.E., and Baker, H.J. 2000. Body composition of growing and adult cats as measured by use of dual energy X-ray absorptiometry. Comparative Medicine, 50:175-183.
Lautenschlager, S. 2013. Cranial myology and bite force performance of Erlikosaurus andrewsi: a novel approach for digital muscle reconstructions. Journal of Anatomy, 222:260-272.
doi:10.1111/joa.12000
Leidy, J. 1853. Description of an extinct species of American lion: Felis atrox. Transactions of the American Philosophical Society, 10:319-321.
Mazák, J.H., Christiansen, P., and Kitchener, A.C. 2011. Oldest known pantherine skull and evolution of the tiger. PLoS ONE, 6:e25483.
doi:10.1371/journal.pone.0025483
Meachen-Samuels, J. and Van Valkenburgh, B. 2009. Forelimb indicators of prey-size preference in the Felidae. Journal of Morphology, 270:729-744.
doi:10.1002/jmor.10712
Munday, H.S., Earle, K.E., and Anderson, P. 1994. Changes in the body composition of the domestic shorthaired cat during growth and development. Journal of Nutrition, 124:2622S-2623S.
Persons IV, W.S., Currie, P.J., and Norell, M.A. 2013. Oviraptorosaur tail forms and functions. Acta Palaeontologica Polonica, 59. doi:10.4202/app.2012.0093.
Pitts, G.C. and Bullard, T.R. 1968. Some interspecific aspects of body composition in mammals, p. 45-70. Body Composition in Animals and Man. National Academy of Science, Washington, D.C.
Randau, M., Goswami, A., Hutchinson, J.R., Cuff, A.R., and Pierce, S.E. 2016. Cryptic complexity in felid vertebral evolution: shape differentiation and allometry of the axial skeleton. Zoological Journal of the Linnean Society, 178:183-202.
doi:10.1111/zoj.12403
Sellers, W.I., Hepworth-Bell, J., Falkingham, P.L., Bates, K.T., Brassey, C.A., Egerton, V.M., and Manning, P.L. 2012. Minimum convex hull mass estimations of complete mounted skeletons. Biology Letters, 8:842-845.
doi:10.1098/rsbl.2012.0263
Smith, R.J. 2002. Estimation of body mass in palaeontology. Journal of Human Evolution, 43:271-287. doi:10.1006/jhev.2002.0573
Sorkin, B. 2008. A biomechanical constraint on body mass in terrestrial mammalian predators. Lethaia, 41:333-347.
doi:10.1111/j.1502-3931.2007.00091.x
Sutton, M.D., Garwood, R.J., Siveter, D.J., and Siveter, D.J. 2012. SPIERS and VAXML: A software toolkit for tomographic visualisation and a format for virtual specimen interchange. Palaeontologia electronica, 15.2.5T:1-14 palaeo-electronica.org/content/issue-2-2012-technical-articles/226-virtual-palaeontology-toolkit
Witmer, L.M. 1995. The extant phylogenetic bracket and the importance of reconstructing soft tissues in fossils, p. 19-33. In Thomason, J.J. (ed.), Functional morphology in vertebrate paleontology. Cambridge University Press, New York.
