|
|
|
MATERIALS AND METHODSFinite Element Models
We constructed several kinds of models for both pachycephalosaurs. As a control, to test whether stress distributions might differ simply because the animals varied greatly in size, we scaled the 2D sagittal sections to an identical length (see "forces" below). For a realistic model of the properly scaled Homalocephale, we used the extrude tool in Multiphysics® to expand its profile to the approximate width of the skull (about 6 cm). Two kinds of models were constructed for Pachycephalosaurus. We extruded the Homalocephale-length trace into a sagittal section the same width as the Homalocephale model. To construct a truly domed 3D model we rotated the trace about a line with identical y-coordinates near those of the trace's ventral base (parallel to the x-axis) and with endpoints at their respective x-coordinates. Another pachycephalosaurine model, based on a subadult (Museum of the Rockies MOR 453) sectioned by Goodwin and Horner (2004), was constructed as a materially realistic replication of Sues's (1978) Plexiglas tests. This model allowed us to check the effects of a zone of trabecular bone on compressive stress and strain. We tested the hypothesis that if trabeculae resisted compression, a region of cancellous bone would exhibit low strain magnitude. In an essentially 2D model of a section of its dome (set to 1 mm thickness), we embedded a subdomain corresponding to the cancellous Zone II (Fig. 3A in Goodwin and Horner [2004]), and assigned appropriate material properties to all three zones. This model is based on a midsagittal histological section that did not extend completely through the dome. We restored the posterior portion as roughly symmetrical to the sectioned anterior portion, which may have resulted in an anterioposteriorly compressed model. A refined model would give more realistic results for stress distribution, but would not change the effects of varied material properties on relative strain magnitude. At present we cannot characterize the morphology of keratinous integument covering the dome (Goodwin and Horner 2004; although in some specimens the pattern of vascular canals suggests supply to a mosaic of hexagonal scales). We therefore added keratinous zones of three different thicknesses to the model of the subadult pachycephalosaurine, to test the sensitivity of bone stress to inference of integumentary morphologies. The models were meshed at varying resolutions in COMSOL Multiphysics®, using the mesh parameters and "remesh" options. Unusually large, small, or otherwise problematic meshes can result in stress artifacts or even solution failure. We ran analyses iteratively until we achieved results with the highest resolution mesh possible without a significant drop in solution time or performance. For example, our Homalocephale model had 20736 elements, and the Pachycephalosaurus dome mesh had 13732; the latter experienced errors at higher element numbers. Solutions at equivalent node positions converged in meshes of 5000 elements or more, and we have no reason to doubt the accuracy at other positions for larger meshes. Material Properties
Measurements of bone material properties vary depending on the bone's histology and the measurement protocol. We therefore assigned elastic modulus (stress-strin relationship E=20 GPa), Poisson's ratio (transverse versus longitudinal strain
For the subadult pachycephalosaurine model we assigned the above properties of compact bone in the deep and superficial histological zones I and III (Goodwin and Horner 2004). For the cancellous zone II, we assigned an appropriate elastic modulus of E=8 GPa, a density
Impact Forces and Displacement Boundary ConditionsDuring an impact, each pachycephalosaur's kinetic energy would dissipate over a distance, yielding an impact force (Alexander 1989):
where m is the mass of the animal, v is the closing speed, and d is the deceleration distance. We used one fast and one slower closing speed for both species: 6.7 and 3 m/s, respectively. The former was considered a reasonable "maximum" collective closing speed for the pachycephalosaurs, given their likely hip heights and limb proportions. (It is also the highest observed speed of collisions that inspired this study, between American football players coached by the second author.) The mass for Homalocephale was set to 36 kg (a volumetric model estimate courtesy Paul, personal commun., 2006) and that of Pachycephalosaurus at 488 kg. For the latter mass, we scaled Gregory Paul's volumetric estimate (personal commun., 2006) for a smaller specimen (Russell 1995) to the size of the modeled AMNH specimen, by cubing the ratio of their skull lengths. (The smaller specimen is on display as a pair of cast skeletons [NSM PV 20423, 20424] at the National Science Museum, Tokyo, Japan.) Deceleration distances were more problematic to estimate. Flexion of the vertebral column would account for some of this distance, but the tongue-in-groove zygapophyseal articulations between vertebrae would moderate the displacement. In preserved sequentially paired vertebrae of Stegoceras validum (UALVP 2), the "tongue" of the postzygapophysis can shift 0.3-0.5 cm until it hits a stop facet in the groove of the succeeding prezygapophyses. For the similarly-sized Homalocephale colathoceros, we considered 0.12 m to be a reasonable value for d, but also applied half and double this value to equation 1 to derive a sensitivity range of forces. The longer distance may be especially realistic if a combatant absorbed some of the collision force with its hind limbs. Based on comparisons of skull length, we set the base deceleration distance in Pachycephalosaurus to 0.33 m and varied it around this value as with Homalocephale. Calculated force magnitudes are listed Table 1. We applied these magnitudes to the modeled cranial elements perpendicular to the impacted surfaces. Two different force distributions were applied to the Homalocephale model. One was a point load and the other an edge load applied to a region just above the orbits, assuming a widely-spread impact. Because the Homalocephae model sloped downwards anteriorly, we applied x and y vector components of the estimated resultant force. For Pachycephalosaurus we applied head-on forces to a point at the apex of the dome using a point force application. The resulting stress seemed low, so we applied the force as if focused onto one square centimeter (multiplied by 10,000). This method is not strictly correct, but we wished to cover potential underestimates in our procedures. For the Pachycephalosaurus side-impact test, we applied a high force (at 6.7 m/s and 0.33 m deceleration distance) perpendicular to a broad area of the dome's lateral surface, simulating an impact to an opponent's rib cage. The subadult pachycephalosaurine (MOR 453) model was based on a 2D sagittal section. Without a reliable mass estimate, we simply applied a compressive force of –1000 N (y-axis) to its dorsal-most edge. For all three specimens, we restricted the ventral boundaries of the models to an initial displacement of 0. Phylogenetic Analysis and Character Optimization for Pachycephalosauria
|
|
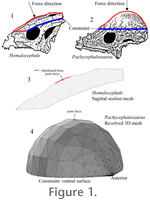 Figure 1
Figure 1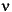 =0.4), and density (
=0.4), and density (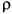 =2000 kg/m3) that fall within the range commonly reported for compact bone.
=2000 kg/m3) that fall within the range commonly reported for compact bone.
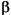 -keratin (E=2.5 GPa,
-keratin (E=2.5 GPa,