Volume density diagrams

Mining morphological evolution in microfossils using volume density diagrams

Michael W. Knappertsbusch and Yannick Mary

Article number: 15.3.7T
https://doi.org/10.26879/278
Copyright Paleontological Society, September 2012

Author biographies
Plain-language and multi-lingual abstracts
PDF version

Submission: 24 March 2011. Acceptance: 16 January 2012

{flike id=282}

ABSTRACT

A technique is explored to visualize series of bivariate morphometric measurements of microfossil shells through geological time with the help of 3D-animated volume-density distributions. Visualization tests were performed using two existing and published sets of morphometric data, i.e., the Neogene coccolithophorid group Calcidiscus leptoporus-Calcidiscus macintyrei and the planktonic foraminifera plexus of Globorotalia menardii. The technique converts series of downcore bivariate morphometric shell data into a continuous frequency distribution, which can be investigated with the help of a graphical data mining tool called Voxler from Golden Software. This tool allowed us to compose and animate complex subsurface structures raised from morphometric measurements of microfossils, and so provides an intuitive, comprehensive insight into the structure and dynamics of complicated evolutionary patterns. With upcoming future large morphometric data sets for oceanic microfossils, this instructive illustration method may hopefully serve to raise more interest in studying topics like morphological evolution, speciation and advances to achieve more universial species concepts needed so strongly in paleontology. An important conclusion from the experiments is that the structure of size frequency distribution through time shows a stronger differentiation into separate morphotype clusters in the coccolith example than in the case of the investigated planktonic foraminifers. The difference between the groups is explained by the differences in ontogenetic shell growth between the alga C. leptoporus and the foraminifer G. menardii. These differences have implications for morphotype classification and evolutionary research by means of morphometry with coccolithophorids and foraminifers.

Michael W. Knappertsbusch. Natural History Museum Basel, Augustinergasse 2, 4001-Basel, Switzerland. michael.knappertsbusch@unibas.ch 
Yannick Mary. Natural History Museum Basel, Augustinergasse 2, 4001-Basel, Switzerland. pelagos@hotmail.fr

KEY WORDS: microfossils; Calcidiscus leptoporus; Globorotalia menardii; morphological evolution; data mining; volume density plots

Final citation: Knappertsbusch, Michael W. and Mary, Yannick. 2012. Mining morphological evolution in microfossils using volume density diagrams. Palaeontologia Electronica Vol. 15, Issue 3;7T, 29p;
palaeo-electronica.org/content/issue-3-2012-technical-articles/282-volume-density-diagrams

INTRODUCTION

Detection of speciation in the sedimentary record is of great importance for the development of species concepts (Miller, 2001), for the recognition of heterochrony (Quillévéré et al., 2002), and for practical chronostratigraphic applications, see concepts discussed in Hottinger (1962), Kennett and Srinivasan (1983), and MacGowran (2005). The validation of species concepts requires heavy statistical bi- or multivariate morphometric analyses to understand the biogeography of speciation globally and over extended geological time. Just recently there was an urgent demand for morphometric analyses for the identification of representative exemplars when foraminiferal holotypes are to be assigned to specimens from an assemblage during description of new species (Scott, 2011). Among all fossil remains those of microfossils like planktonic foraminifera or calcareous nannoplankton are the most promising study objects, obviously because of their abundance and preservation, stratigraphical potential, significance for paleoenvironmental reconstruction and a high morphological variability. Morphometric statistics in foraminifera have existed for at least three quarters of a century (Schmid, 1934), but digital imaging techniques from the 1980s onwards have revolutionized the area because data collection and processing became more efficient. Examples of advanced automated image capturing and measurement techniques for microfossils include Hills (1988), Young et al. (1996), Bollmann et al. (2004) and Knappertsbusch et al. (2009). As a result numerous classical studies about the biogeographic and temporal variability of oceanic pelagic microfossils emerged in the micropaleontological literature, e.g., Kellog (1975), Lazarus (1986), Malmgren and Berggren (1987), Bollmann et al. (1998), Malmgren and Kennett (1982), Malmgren et al. (1983), Kucera and Malmgren (1996), Norris et al. (1996) and Schmidt et al. (2004) to name just a few. The majority of them are based on univariate measurements disregarding the multivariate nature of morphological variability. Results are traditionally illustrated as deviations from the sample means or as univariate histogram series in two-dimensional media. This kind of mediation makes it difficult to communicate complicated shell-variation on a sub-sample level, which, however, is necessary in order to distinguish between the subtle morphological trends of closely related taxa (see the discussion in Kucera and Malmgren (1998) on this argument). There exist many such morphometric time-series studies including more recent literature (Backmann and Hermelin, 1986; Young, 1990; Giraud et al., 2006; Tremolada et al., 2008; Yamasaki et al., 2008). If time-series were inspected on a sub-sample level and if bi- or multivariate data sets were applied more commonly, a more refined morphotype classification can eventually be obtained, which improves recognition of evolutionary patterns. The price for the application of advanced statistical techniques, however, is that communication to non-specialists becomes eventually challenging.

The Case of the Coccolithophorid Calcidiscus leptoporus and Its Descendents

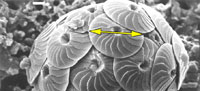
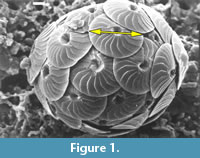Such difficulties were experienced in an extended morphological investigation about the coccolithophorid plexus Calcidiscus leptoporus-Calcidiscus macintyrei more than two decades ago (Figure 1, Knappertsbusch, 1990). This complex comprises at least three extant and several extinct morphotypes that can be distinguished on the basis of the coccolith morphology, namely measurements of coccolith size and number of elements in the distal shield. Recognition of biogeographic and stratigraphic morphovariants was greatly facilitated through the construction of contoured bivariate frequency distributions of coccolith diameter versus its number of elements in the distal shield.

History of Illustration of C. leptoporus Measurements

The strategy of using contour diagrams for the search of morphovariants proved to be promising, because in Holocene sediments modal shifts of coccoliths between samples could be interpreted as the mixing to a various degree of "end-members" across temperature gradients (Knappertsbusch et al., 1997). Particularly, in the living plankton and in Holocene surface sediment assemblages, three extant morphotypes "Small" (S), "Intermediate" (I) and "Large" (L) could be identified in the above study, of which morphotypes I and L were later discovered to represent two different species C. leptoporus and C. quadriperforatus, respectively, on the basis of combined evidence from coccolith morphology, life cycle observations, distribution, ecology and molecular genetics (Quinn et al., 2004; Saez et al., 2003; Geisen et al., 2002), while the specific status of morphotype S still remains unclear (Cortes, 2000; Quinn et al., 2003, Young et al., 2003).

For the downcore study of ancient morphotypes of C. leptoporus and closely related extinct C. macintyrei such biological evidence is not applicable, which renders the differentiation of morphotypes more complicated, especially when morphotypes showed morphological overlap at distant times. Such taxonomic problems could partially be resolved through a careful analysis of the frequency mode shifts from one time-level to the next resulting in a phylogenetic tree of morphotypes within the C. leptoporus-C. macintyrei plexus (Knappertsbusch, 2000). But also this approach was only partially satisfactory because it depends on an artificial, a priori classification of morphotypes. To circumvent a pre-defined classification and in order to better record cladogenetic splitting and phyletic divergence patterns, morphotypes were no longer characterized by their modal coordinates. Instead, a base-line contour was chosen per frequency mode, which encloses the majority of the measured specimens of a particular morphotype. The technique was applied downcore in a number of selected DSDP sites, which helped to construct an envelope of morphotype evolution of C. leptoporus and its descendents by animations (see figures 6 through 9 in Knappertsbusch, 2001), which was not possible during the late 1990s. At those early times computer graphical experiments and spinning scatter diagrams about a coordinate axis were created using MacSpin software, which today no longer exists. Although educational to the investigator, these experiments proved to be difficult to visually interprete to non-specialists and were technically impossible to publish. Knappertsbusch (2001) returned to that difficulty and could for the first time demonstrate the stunning complexity of morphological variability of coccoliths by on-line publishing gif-animated stacks of base contourlines of coccolith frequencies through time.

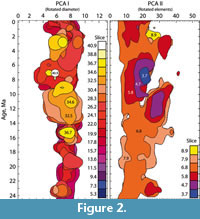By doing so, it was realized, that selection of an arbitrary base contourline might also be too selective for a general description of the full morphometric data body. An alternative was found, where local coccolith frequencies within the morphospace of coccolith diameter and number of elements were interpolated between neighboring samples along the geological time axis. This interpolation was done by discretizing the continuous axes of coccolith diameter and number of elements into classes Delta X and Delta Y, respectively, and coccolith frequencies were counted per grid-cell having a length of Delta X and a width of Delta Y. Interpolation of local frequencies along the time axis created volume elements (voxels), each of which spanned by Delta X, Delta Y and a time increment Delta Z. In this sense a voxel represents the local frequency of coccoliths per volume-element, leading to a spacial density distribution of all measured coccoliths in the morphospace of diameters, number of elements and geological age. For visualization of the model vertical slices parallel to the time axis were then constructed through the model revealing a clear divergence of extra-large coccoliths during the Late Miocene (Figure 2).

Although achieving independence from the previous artificial morphotype classification scheme the described method still remains difficult to digest for non-specialists. The above progress motivated to search for alternative data mining- and display techniques that allow better visualization of the internal structure of the three-dimensional coccolith density distribution.

The Case of menardiform globorotalids (planktonic foraminifera)

A similar morphometric investigation was more recently carried out with the Neogene planktonic foraminiferal plexus of menardiform globorotalids (Figure 3). Again, it was attempted to investigate evolutionary tendencies of present and ancient members of this group by means of quantitative morphometric characterization using the Caribbean DSDP Site 502 and the eastern equatorial Pacific DSDP Site 503 as testing areas (Knappertsbusch, 2007), and a global morphometric survey about modern menardiform globorotalids was realized by Brown (2007). In both investigations a similar bivariate approach was followed to recognize morphotypes as was done for C. leptoporus: Primary measurements consisted of the spiral height (delta x) versus the length of the shell in side view (delta y). These measurements were gridded to obtain bivariate frequency distributions. Modal trends were subsequently analysed by comparison of frequency plots in samples at successive stratigraphic core levels at or from different locations in the global Holocene sample collection.

The two abovementioned studies use fundamentally different groups of unicellular calcareous plankton: In the first case C. leptoporus is autotrophic, and numerous coccoliths were continuously produced during the individual's heterococcolithic life-cycle phase. In the second case G. menardii is heterotrophic, and discontinuous accretion of new chambers is building the shell as the individual maturates. While in C. leptoporus coccoliths cannot be used for unraveling life-history, ontogenetic growth is fully preserved in the foraminiferal test. This has implications for the interpretation of modal shifts in frequency distributions of coccolithophorids versus planktonic foraminifera. In order to also illustrate the differently structured models the abovementioned data of G. menardii will be portrayed in the following section using the same method as applied with C. leptoporus.

We were therefore seeking for methods to quantitatively recognize, analyze and document similarities and differences in morphological patterns, assuming that evolution is driven by common, superior biological processes. In this context an interesting graphical data mining tool called Voxler from Golden Software (www.goldensoftware.com) came to our attention. This software is usually applied in exploration for natural resources (for example in mapping subsurface metal concentrations), geophysics, oceanography, astronomy or in clinical applications (modeling of bone-density in x-ray computer tomography). Unfortunately, such tools are barely exploited by paleontologists or taxonomists to illustrate their observations. Voxler allows displaying rendered volume densities (voxels) of properties in multidimensional space, which can be animated on the computer monitor for visual inspection. This tool was found especially instructive for the visualization of the C. leptoporus-C. macintyrei and G. menardii data sets.

The present contribution is purely technically motivated and thus reports on the advantages of volume density analysis and illustration using the abovementioned, earlier published C. leptoporus- and G. menardii data sets as showcased for the method. A taxonomic review of the presented taxa, however, is beyond scope here, and the reader is referred with this respect to the cited original research.

METHODS

Basic Data Sets

In the following sections the transformation of the primary bivariate measurements that were collected for C. leptoporus and G. menardii into four-dimensional voxels is summarized. Recall, that a voxel represents the abundance (frequency F) of specimens in a local volume element, which is defined by intervals of two morphometric measurements (Delta X for coccolith diameter, Delta Y for number of elements in C. leptoporus; delta x for spiral height, delta y for axial length in G. menardii) and geological age (Z). For reasons of brevity the procedures for collection of the primary morphometric data are not repeated here, as they can be read from the cited publications. The necessary auxiliary programs to construct the data models and all derived results are delivered as archives that can be downloaded for further experimentation (see Appendix).

Calcidiscus leptoporus

Primary measurements of the plexus of C. leptoporus and C. macintyrei consisted of the diameter of the circular coccoliths (X) versus the number of the sinuoisal elements (Y) in their distal shields (Figure 1). They were collected by electron microscopy from Holocene surface sediments and a number of deep-sea drilling cores some extending back to 24 million years ago. Whenever possible, it was attempted to measure 200 coccoliths or more per sample to obtain a reasonable statistical basis. At that sample size morphotypes can be expected to be found with a probability of 95%, if their true relative abundance within the sediment assemblage was larger or equal to 2% (Hay, 1972; Knappertsbusch et al., 1997). The geographic provenance of the samples and core locations, their numerical age determinations, taxonomic concepts, morphometric procedures and measurements are all extensively documented in Knappertsbusch et al. (1997), Knappertsbusch (2000) and Knappertsbusch (2001).

Globorotalia menardii

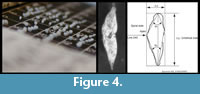Also in the study of G. menardii individuals were characterized using bivariate measurements, i.e., the spiral height (delta x) versus the axial length (delta y) of the shell in side view (Figure 4).

For the G. menardii study, samples were chosen at selected levels between 8 Ma through the Late Pleistocene from the two DSDP Sites 502 (Caribbean Sea) and 503 (eastern Equatorial Pacific). Morphometric measurements were collected by manually positioning and orienting the specimens that were mounted in keel-view in multi-cellular slides under a binocular microscope. The microscope was connected to a digital imaging system for capturing images, processing, extraction of outline coordinates and morphometric data extraction (see Knappertsbusch, 2007). The investigated number of specimens had to be reduced here because of the limited availability of foraminiferal shells in few samples. If possible the number of measured specimens was between 75 to over 100 per sample. A detailed description of the sample preparation-, image capture-, measurement- and analysis protocols is given in Knappertsbusch (2007) together with the numerical age estimates of the samples.

From Scatter-data to Volume Density Surfaces

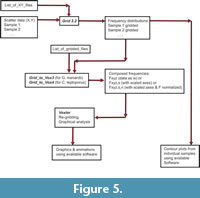Construction of Volume Density Surfaces for Calcidiscus leptoporus. This section explains the transformation from scattered data to density surfaces, for which the C. leptoporus data set is used, but the same procedure was applied to G. menardii as well. The scheme in Figure 5 summarizes the sequence of software applications to arrive at volume density diagrams developed in this and the following sections.

When plotting original values of X (coccolith diameter) against Y (number of elements) one single or several clusters appear from one sample to the next, which, in the case of C. leptoporus, were assigned to morphotypes (Knappertsbusch et al., 1997, Knappertsbusch, 2000). These clusters were identified with the help of contoured bivariate frequency distributions. This identification was achieved by first "gridding" the X,Y measurements. The scattered data were mathematically overlain by a mesh of rectangular grid-cells with the number of specimens counted per grid-cell per sample leading to bivariate frequency distributions. In C. leptoporus each grid-cell had a length of Delta X = 50 micrometers in X- direction and a width of Delta Y = 2 elements in Y-direction (Figure 6.1) (see also Table 1). In practice gridding was performed with an auxiliary program called Grid2.2 written in Fortran (see Appendix for a listing and an executable application). Grid2.2 allows to batch-process large series of input files, each of them containing the cartesian X,Y measurements per sample, i.e., one pair of X,Y measurements per specimen. The output from Grid2.2 is a 14 x 27 matrix for every sample containing the frequencies of coccoliths per grid-cell (coccolith diameters are sorted into 14 columns, and the number of elements are sorted to 27 rows). These "gridded files" were converted to contour diagrams using commercial software (such as Surface III+, Surfer, or Origin 8). Contour diagrams are ideal for the comparison of modal shifts within an assemblage (Figure 6.2) and has led to the numerical classification of morphotypes described in Knappertsbusch et al. (1997) and Knappertsbusch (2000). For improvement of visibility of the internal structures, the coordinate axes were scaled to attain values between 0 and 1 (Figure 6.3). Actually, this normalization was carried out while merging all samples together using a second auxiliary Fortran program called Grid_to_Vox4 (applicable to C. leptoporus; see more explanations about normalization in the sections further below). Gridding and normalization was done for every sample downcore leading to a stack of frequency distributions of the coccoliths (see a sketch of such stacked contour representations in Figure 6.4). In this manner evolutionary tendencies become visible through connecting mode centers or basal contour lines from one time level to the next (see Knappertsbusch, 2001). In order to investigate internal structures in more detail a continous data model was constructed from the series of gridded files from all cores and the modal dynamics through time shown as iso-surfaces of constant coccolith frequencies. This model was analyzed using Voxler software and by re-gridding the global set of normalized frequency distributions in X-, Y- and Z direction (to achieve spacial interpolation of frequencies at finer resolution), thus allowing the generation of series of iso-surfaces, which shows the internal geometry of this hyperspace defined by the morphological parameters, geological age and coccolith frequency. An example for the "outer skin" of this data model is illustrated in Figure 6.5. Experimentation with Voxler has confirmed that the so generated iso-surfaces follow the topology of the phylogenetic tree developed in Knappertsbusch (2000). Figure 6.6 shows an animated overlay of this phylogenetic tree with the rendered iso-surface of Figure 6.5.

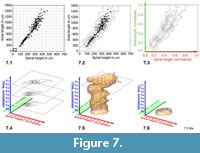Construction of Volume Density Surfaces for Globorotalia menardii . The construction of density isosurfaces of G. menardii was done in a similar manner. The expectation was that the G. menardii plexus would also disintegrate into several recognizable morphotype-clusters as was experienced with C. leptoporus. However, as Figure 7 (see also Table 2) shows for shell measurements from DSDP Site 502 (Caribbean Sea), the nature of the distribution is quite different (see sections further below for a brief discussion on this phenomenon). Similar to C. leptoporus the original data for G. menardii consisted also of bivariate measurements, i.e., spiral height (x) versus axial length (y) in profile view (Figure 4). The data shown is identical to the one presented in Knappertsbusch (2007). Bivariate frequency distributions were derived from scatter using auxiliary program Grid2.2 at grid-cell dimensions of delta x = 50 micrometers in x-direction and delta y = 100 micrometers in y-direction (Figure 7.1). These dimensions were found upon experimentation and on the basis of statistical rules discussed in Keating and Scott (1999), Hyndman (1995), and Jenkinson and Smith (2000). And, similar to C. leptoporus, contour diagrams were constructed for each sample (Figure 7.2) and axes normalized (Figure 7.3) while combining all gridded files into one data model with auxiliary Fortran program called Grid_to_Vox3 (version applicable for G. menardii, see Appendix). The sketch in Figure 7.4 shows a contour stack from normalized distributions at three subsequent stratigraphic levels. Again, the numerical stack was fed to Voxler, re-gridded, and then local frequencies of menardiform specimens were visualized using the iso-surfaces tool in Voxler. Figure 7.5-7.6 show the rapid expansion of the G. menardii hyperspace during the last quarter of the time, which coincides with the gradual closure of the Isthmus of Panama.

Preparation for Input to Voxler: Composing Bivariate Frequency Distributions. As can be seen from Figure 6 and Figure 7 Voxler allows displaying multidimensional datasets in three-dimentional form of rendered animated iso-surfaces on a computer monitor. This tool is extremely helpful for mining of subsurface data structures like evolutionary patterns. The input into Voxler is numerical data that can be prepared in spreadsheet format. In the present contribution the two auxiliary Fortran programs Grid_to_Vox3 (for G. menardii) and and Grid_to_Vox4 (for C. leptoporus) composed the data model from gridded files (see Figure 5) and formatted them into four columns, i.e., Delta X, Delta Y, Z, and F: Delta X (the bin-width of the frequency distribution in X-direction), Delta Y (the bin-width of the frequency distribution in y-direction) are arranged in ascending order. The value Z represents the age of the sample in million years and is sorted from young to old. In the last column, F is listed, which is the local frequency of specimens in a sample per grid-cell. A complete four-dimensional data model of Delta X, Delta Y, Z and F is composed from downcore series of gridded samples for G. menardii or C. leptoporus. Numerical ages for each sample were fed to the Grid_to_Vox programs via an external input file called list_of_file, which contains the names of all gridded sample files and their associated absolute ages. Gridded frequencies of specimens per sample were obtained using program Grid2.2 described in the previous section. Listings and executable applications for Grid_to_Vox3 and Grid_to_Vox4 on PC are also provided in the appendix.

A Comment about Normalization. A direct plot of the untreated data model would not produce any interpretable visualization of internal structures because of the different units involved. This is the reason why Delta X-, Delta Y-, Z-, and F values needed to be normalized. This procedure is performed within the two auxiliary programs Grid_to_Vox3 (for G. menardii) and Grid_to_Vox4 (for C. leptoporus). In these programs morphometric axes (X,Y) were normalized so that they attain values between 0 and 1: In the case of C. leptoporus the original axes of diameter (X) and the number of elements (Y) range from 0 through 14 micrometers and from 0 through 54 elements, respectively (see Figure 6.1). Because the length Delta X of the grid-cell was chosen at 1 micrometer, the center of the first grid-cell has an X-coordinate of 0.5 micrometer and the last grid-cell has an X-coordinate of 13.5 micrometers. Similarly, the centers of the lowest and uppermost grid-cells along the axis of number of elements have Y-coordinates at 1 element and 53 elements, respectively (Delta Y being 2). For this reason, X-values of the X, Y, Z and F-quadruple were divided by 13.5, and Y-values were divided by 53. This rescaling leads to ranges between 0 and 1 along both axes (see Figure 6.3). The Z values (time axis) were divided by -23.08, which is the age of oldest sample of the C. leptoporus sample set. This procedure yields scaled age ranges between 0 (present) and -1 (corresponding to an age of 23.08 Ma). Also the frequency F was subjected to normalization when gridded data were reformatted for Voxler input with the two versions of the Grid_to_Vox programs: F can be chosen to be in absolute or relative (in percentages) frequencies. Absolute frequencies are applicable if the number of specimens per sample remains constant throughout the entire data set. Otherwise, relative frequencies can be determined in order to maintain trans-sample comparability. In the examples presented here relative frequencies were calculated by division of the absolute frequencies per grid-cell per sample by the total number of specimens in that sample.

In G. menardii the normalization occurred analogously by division of values along the x- and y-axes through 675 micrometers and 1550 micrometers, respectively, again leading to ranges from 0 to 1 for both axes. Ages were divided by -8 my, because this is the oldest age of G. menardii described in Knappertsbusch (2007). In the visualizations for G. menardii the normalized ages thus range from -1 (corresponding to an age of 8 Ma) to 0 (Recent). Normalization of frequencies was realized in the same way as was done with C. leptoporus. The applied normalization is simple; more sophisticated methods of trans-sample normalization is feasible, for example through the construction of pareto density estimates, a technique developed by mathematicians for mining and visualization of density structures in higher dimensional data (Ultsch, 2003; Shoval et al. 2012), but this is beyond the scope of the present contribution.

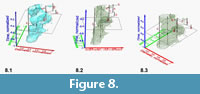Input to Voxler and Graphical Data Display. Once the data are gridded, composed, normalized and re-arranged to four columns in the above described way, they can be imported into Voxler. A single record line of Delta X, Delta Y, Z and F represents now a volume density value (Voxel), i.e., the frequency F (absolute or relative) of specimens in a volume spanned by units of Delta X and Delta Y, and the associated age. Note, that at this stage an "interval" of time from a particular sample represents still a time-plane, i.e., it has no real depth along the time axis. Using the "gridding" command in Voxler, frequencies are interpolated from sample to sample and in direction of the X- and Y-axes, which results in discrete volume densities. Using the graphical modules in Voxler three-dimensional iso-surfaces of equal frequencies of specimens through time or in sections with any plane are created. This method allows the exploration of the morphospace of a species' shell variability in an unprecedented manner: Parts of the data model, that in a two-dimensional representation would overlap suddenly appear as separate, branching density cloud when observing under various angles of view. Figure 8 illustrates such a speciation event for the plexus of C. leptoporus-C. macintyrei using a rotating isosurface captured at an arbitrarily chosen isovalue of 1.52, which was composed from measurements from all DSDP and ODP sites described in Knappertsbusch (2000) and Knappertsbusch (2001). Note the distinctive separation into an extinct branch ending in large morphotypes D and A (C. macintyrei) while the extant branch (C. leptoporus) ends in the morphotypes S, I and L. 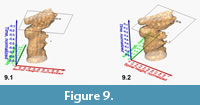The prominent restriction in the middle of the isosurface corresponds to the disappearance of extra-large Miocene morphotype D. The stratigraphically important extinction level of C. macintyrei appears as a small separate cloud in the upper part of the diagram.

Figure 9 shows a similar example for a spinning animation of the normalized, interpolated frequency isosurface for G. menardii from DSDP Site 502 (Caribbean Sea). In this case, the morphospace is spanned by the axes of spiral height and axial length, and the time extends over the past 8 million years. Morphometric measurements for this model were taken from Knappertsbusch (2007).

PLAYING WITH THE DENSITY SURFACES

Involved Density Surfaces

The Voxler software allows graphical comparison of involved isosurfaces that come from different locations, which is illustrated for G. menardii in Figure 10.1-3 from DSDP Site 502 (Caribbean Sea) and DSDP Site 503 (eastern equatorial Pacific).

Pulsating Volume Density Surfaces

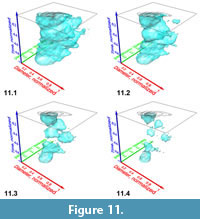
Iso-surfaces with a high iso-value enclose voxels with abundant specimens and so represent the most typical morphology of the assemblage.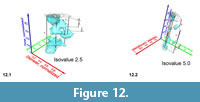 In contrast, low-level iso-surfaces enclose morphologies that occur rarely in the distribution, and they represent the morphological extremes of the investigated group through time. The analysis of intermediate, internal density structures is interesting if one is out to investigate patterns of morphological divergence through time. Figure 11 shows frequency iso-surfaces for C. leptoporus at four decreasing iso-values: At an iso-value of 0.5 (low frequency) a single surface envelopes the all coccoliths of C. leptoporus and C. macintyrei. 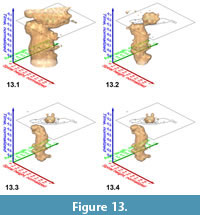As isovalues increase, the single surface disintegrates into an ancestral root and descendent separate clouds, which coincide with branches of the previously developed phylogenetic tree. Figure 12.1-2 shows such animated frequency iso-surfaces of C. leptoporus under different aspects of view.

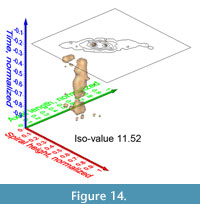Similar pulsating iso-surfaces were created to illustrate the internal frequency trends through time for G. menardii during the past 8 million years: Figure 13.1-4 shows changing density surfaces at four increasing isovalues at DSDP Site 502 (Caribbean Sea). The animation in Figure 14 demonstrates the remarkably stable ancestral portion of comparably small G. menardii until about 1.8 Ma (corresponding to a value of 0.23 on the normalized time axis). Thereafter, G. menardii started to strongly increase in size (compare also with Knappertsbusch, 2007, figure 10).

LIMITATIONS

The present study exploits morphometric data about C. leptoporus and G. menardii and evaluates volume density plots to explain patterns of evolution to a wider audience. A requirement for the construction of volume density plots is the availability of constant and statistically sufficiently high numbers of specimens at regularly spaced time intervals throughout the investigated timespan. In this context "constant" means that specimen numbers should ideally not vary from sample to sample in order to maintain distributions comparable from one time level to the next. On the requirement of "statistically sufficient" specimen numbers in quantitative analyses there is debate among authors: While Buzas (1979) recommended a minimum of 300 specimens per sample, Fatela and Taborda (2002) concluded that treatment of only 100 specimens provides satisfactory statistical reliability in a large number of paleoceanographic studies. Consulting the nomogram published in Hay (1972), which relies on a unimodal binomial distribution model, 300 specimens are allowed to detect morphotypes that occur at 1% in the assemblage with a probability of 95%. In case of multimodal distributions, different models need to be applied but following exemplified cases given in the recent literature sample sizes did not exceed 100 specimens per sample neither (Heslop et al., 2011). Often, the researcher is faced with uneven sampling, i.e., most of the available samples provided enough specimens while there are few samples, where this requirement is not met at a satisfactory level. A particular difficulty is that the presence of several morphotypes per sample calls for proportionally increasing numbers of specimens to be investigated, which increases the labour to be done in the course of a running project. Uneven sampling can, however, (partially) be overcome by normalization or rarefaction, or through "split-weighting," as was applied in Knappertsbusch (2007). The generation of frequency distributions relies on a reasonable choice of bin-widths, which itself influences the required minimum sample size, and which in our case was estimated following the formulae given in Keating and Scott (1999); Hyndman (1995) and Jenkinson and Smith (2000) and upon own experimentation. In summary, entering a compromise between Buzas (1979) and Fatela and Taborda (2002), sample sizes of 200 specimens in our C. leptoporus experiment and between 75 and 100 specimens per sample in our G. menardii case were considered a reasonable balance between efficiency of the study and the accuracy of the results.

CONCLUSIONS

Educational Potential of Volume Density Diagrams

While in two-dimensional media the true complexity of morphological patterns through time remains often obscured modern graphical techniques like volume density surface plots are capable to document evolutionary trends more intuitively than any sophisticated statistical package. Visualization difficulties with complex data recur commonly in natural science disciplines like medicine or astronomy and are currently a hot topic in software development labs (Reed, 2011; Service, 2011; Rowe and Frank, 2011). There is an extended scientific literature on data visualization methods (refer for example to the annotated bibliography of the Computer Vision Informatics Pages under http://www.visionbib.com/bibliography/stereo431.html), however, the cited sources often require profound background knowledge in mathematics and/or informatics to be immediately applicable to micropaleontological problems. On the other hand, traditional methods, such as displaying stacks of scattered data or plots of sample means published in most of the micropaleontological literature do not sufficiently provide the true nature of the sometimes surprisingly complex phylogenetic pattern. The illustrated experiments with Voxler using C. leptoporus-C. macintyrei data is in our opinion an impressive example for the outstanding educational potential of volume density analysis in morphometry and evolutionary research. It can thus be expected that three-dimentional analysis and visualization opens a new frontier in (micro)paleontology, not only for surface reconstructions of objects but also for extended data sets from downcore measurements.

Downcore frequency-mining through size classes clearly shows advantages. There is no better means to visualize evolutionary change within subsets of fossil populations that simultaneously include in their phylogenies components of stasis, directional change, increase of variance or divergence. Especially in C. leptoporus, where morphotypes can relatively easily be recognized by modal analysis morphological divergence on sub-generic level is evident. Evolutionary novelty is recognizable in the expansion of the low frequency portion of the morphological spectrum, where extreme but rare forms have developed. For speciation analysis, it is useful to observe this low frequency tail of the distribution along the stratigraphic column. Similar experiences were made by Schmidt et al. (2004) for foraminiferal assemblages, and most recently by Herrmann (2010) for calcareous nannoplankton assemblages on supra-generic level. But also the high frequency portion is interesting to pursue. In this fraction ancestral clusters tend to connect to the more recent ones portraying the basic nature (directional change or stasis) of phylogenetic relationships from continuous data. Under this aspect the presented visualization method helps to better extract phylogenetic trends from ancestral assemblages throughout the remnant survivors within a mélange of morphotypes under changing environments without the necessity of artificial morphotype classification schemes prior to analysis. Only through the comparison of iso-surfaces at varying densities these results came to the surface.

Implications for Evolutionary Studies and Taxonomy

The illustrated examples have implications for future morphometric investigations of evolution. The geometry of the volume density pattern of the coccolithophorid plexus C. leptoporus-C. macintyrei differs from the one in the foraminiferal group G. menardii. In the coccolith example, morphotypes tend to pop up as isolated clusters, with phylogenetic connections via the low frequency portion. In contrast, the foraminiferal example shows, that rather continuity across all density levels is the rule, and cluster formation is subordinate. Such continuity in planktonic foraminiferal frequency distributions is explained by the pronounced allometric shell growth during foraminiferal ontogeny, which is not seen in coccolithophorids. In the opinion of the authors the size-range of heterococcoliths surrounding a cell is rather pre-determined by the genetic makeup of species as was confirmed by life-cycle observations and molecular genetics for extant C. leptoporus (Quinn et al., 2004; Geisen et al., 2004; Sáez et al., 2003), although there are also physiological and nutritional influences on the dimension of the surrounding coccoliths (Henderiks and Renaud, 2004). The consequence of these differences on generic level is that with foraminifera more care must be taken during the analysis with respect to size effects in the ancient population than with calcareous nannoplankton.

The new visualization of the C. leptoporus model illustrates how quite similar coccolith morphologies appear repeatedly at distant geological times - their distinction in one and the same sample, however, remains impossible. The occurrence of clades also has implications for taxonomy because clades always indicate previous speciation. The succession of similar morphoclade expansions separated by extended time intervals makes repetitive evolution likely. The prominent time-transgressive restriction seen in the iso-surface at an isovalue of 1.52 of the C. leptoporus model at the end of the Miocene may serve as an example for this interpretation.

ACKNOWLEDGMENTS

This research profited through amalgamation of ideas and research results from a number of earlier projects over the years. Support was provided from the Swiss National Foundation (Grant Nos. 20-5305.87, 2000-043058.95/1, 2000-050558.97/1, 2000-056875.99/1, 200020-109258/1 and 2100-67970/1, and 200021-121599/1). Continuous support was given by the City of Basel and various contributions from the Natural History Museum in Basel, the Kugler Werdenberg Stiftung in Basel, and the Freiwillige Akademische Gesllschaft in Basel allowed acquisition of the applied equipment and software. The Ocean Drilling Program (ODP) provided the sample materials. Initial ideas emerged during the PhD research of the first author in the micropaleontology group of Hans Thierstein (ETH Zürich). We acknowledge the comments of two anonymous reviewers to improve the manuscript and the continuous assistance of the Palaeontologia Electronica team. There were so many more persons, friends and former colleagues involved giving ideas and discussion that they cannot be mentioned individually, and we wish to thank all of them.

REFERENCES

Backman, J. and Hermelin, O.R. 1986. Morphometry of the Eocene nannofossil Reticulofenestra umbilicus lineage and its biochronological consequences. Palaeogeography, Palaeoclimatology, Palaeoecology, 57:103-116.

Bollmann, J., Baumann, K.-H., and Thierstein, H.R. 1998. Global dominance of Gephyrocapsa coccoliths in the late Pleistocene: Selective dissolution, evolution, or global environmental change ? Paleoceanography, 13:517-529.

Bollmann, J., Quinn, P.S., Vela, M., Brabec, B., Brechner, S., Cortes, M., Hilbrecht, H., Schmidt, D.N., Schiebel, R., and Thierstein, H.R. 2004. Automated particle analysis: Calcareous microfossils, p. 229-252. In Francus, P. (ed.), Image analysis, sediments and Paleoenvironments. Developments in Paleoenvironmental Research, Volume 7. Kluwer Academic Publishers, Springer Verlag, Dordrecht.

Brown, K. 2007. Biogeographic and morphological variation in late Pleistocene to Holocene globorotalid foraminifera. Unpublished PhD Thesis, Universität Basel. pages.unibas.ch/diss/2007/DissB_8290.htm

Buzas, M.A. 1979. The measurement of species diversity, p. 3-10. In Lipps, J.H., Berger, W.H., Buzas, M.A., Douglas, R.G. and Ross, C.A. (eds.), 1979 Foraminiferal Ecology and Paleoecology, SEPM Short Course No. 6, Houston 1979. Society of Economic Paleontologists and Mineralogists.

Cortés, M.Y. 2000. Further evidence for the heterococcolith-holococcolith combination Calcidiscus leptoporus-Crystallolithus rigidus. Marine Micropaleontology, 39:35-37.

Fatela, F. and Taborda, R. 2002. Confidence limits of species proportions in microfossil assemblages. Marine Micropaleontology, 45:169-174.

Geisen, M., Billard, C., Broerse, A.T.C., Cros, L., Probert, I., and Young, Y.R. 2002. Life-cycle associations involving pairs of holococcolithophorid species: intraspecific variation or cryptic speciation? European Journal of Phycology, 37:531-550.

Geisen, M., Young, J.R., Probert, I., Sáez, A.G., Baumann, K.-H., Sprengel, C., Bollmann, J., Cros, L., De Vargas, C., and Medlin, L. 2004. Species level variation in coccolithophores. Coccolithophorid biodiversity: evidence from the cosmopolitan species Calcidiscus leptoporus, p. 327-366. In Thierstein, H.R. and Young, J.R. (eds.), Coccolithophores. From Molecular Processes to Global Impact. Springer, Berlin, Heidelberg.

Giraud, F., Pittet, B., Mattioli, E., and Audouin, V. 2006. Paleoenvironmental controls on the morphology and abundance of the coccolith Watznaueria britannica (Late Jurassic, southern Germany). Marine Micropaleontology, 60:205-225.

Hay, W.W. 1972. Probabilistic stratigraphy. Eclogae Geologicae Helvetiae, 65(2):255-266.

Henderiks, J. and Renaud, S. 2004. Coccolith size increase of Calcidiscus leptoporus offshore Morocco during the Last Glacial Maximum: an expression of enhanced glacial productivity? Journal of Nannoplankton Research, 26:1-12.

Herrmann, S. 2010. Ecological and evolutionary significance of coccolith size changes. Unpublished PhD Thesis, ETH Zürich.

Heslop, D., De Schepper, S., and Proske, U. 2011. Diagnosing the uncertainty of taxa relative abundances derived from count data. Marine Micropaleontology, 79:114-120.

Hills, S.J. 1988. Outline extraction of microfossils in reflected light images. Computers & Geosciences, 14:481-488.

Hottinger, L. 1962. Documents micropaléontologiques sur le Maroc: Remarques générales et bibliographie analytique. Notes du Service Géologique du Maroc, 21(156):7-14.

Hyndman, R.J. 1995. The problem with Sturge's rule for constructing histograms. Unpublished manuscript. robjhyndman.com/papers/sturges.pdf

Jenkinson, M. and Smith, S. 2000. Optimisation in robust linear registration of brain images. FMRIB Technical Report TR00MJ2. Oxford Centre for Functional Magnetic Resonance Imaging of the Brain (FMRIB), University of Oxford, UK www.fmrib.ox.ac.uk/analysis/techrep/tr00mj2/tr00mj2.pdf

Keating, J.P. and Scott, D.W. 1999. Ask Dr. Stats. Stats 25:16-25.

Kellogg, D.E., 1975. The role of phyletic change in the evolution of Pseudocubus vema (Radiolaria). Paleobiology, 1:359-370.

Kennett, J.P. and Srinivasan, M.S. 1983. Neogene planktonic foraminifera. A phylogenetic atlas. Hutchinson Ross Publishing Company, Stroudsburg, Pennsylvania.

Knappertsbusch, M., 1990. Geographic distribution of modern coccolithophorids in the Mediterranean Sea and morphological evolution of Calcidiscus leptoporus. Unpublished PhD Thesis, ETH Zürich, Switzerland.

Knappertsbusch, M. 2000. Morphologic evolution of the coccolithophorid Calcidiscus leptoporus from the Early Miocene to Recent. Journal of Paleontology, 74:712-730.

Knappertsbusch, M. 2001. A method of illustrating the morphological evolution of coccoliths using 3D animations applied to Calcidiscus leptoporus. Paleontologia Electronica, Volume 4, Issue 1, Article 1:12p, 259KB.
palaeo-electronica.org/2001_1/k2/issue1_01.htm

Knappertsbusch, M. 2007. Morphological variability of Globorotalia menardii (planktonic foraminiferan) in two DSDP cores from the Caribbean Sea and the Eastern Equatorial Pacific. Carnets de Géologie / Notebooks on Geology, Article 2007/04 (CG2007_A04).
paleopolis.rediris.es/cg/CG2007_A04/index.html

Knappertsbusch, M., Cortes, M.Y., and Thierstein, H.R. 1997. Morphologic variability of the coccolithophorid Calcidiscus leptoporus in the plankton, surface sediments and from the Early Pleistocene. Marine Micropaleontology, 30:293-317.

Knappertsbusch, M., Binggeli, D., Herzig, A., Schmutz, L., Stapfer, S., Schneider, C., Eisenecker, J., and Widmer, L. 2009. AMOR - A new system for automated imaging of microfossils for morphometric analyses. Palaeontologia Electronica, Volume 12, Issue 2; 2T: 20p, 12.7MB.
palaeo-electronica.org/2009_2/165/index.html

Kucera, M. and Malmgren, B.A. 1996. Latitudinal variation in the planktonic foraminifer Contusotruncana contusa in the terminal Cretaceous ocean. Marine Micropaleontology, 28:31-52.

Kucera, M. and Malmgren, B.A. 1998. Differences between evolution of mean form and evolution of new morphotypes: an example from Late Cretaceous planktonic foraminifera. Paleobiology, 24:49-63.

Lazarus, D. 1986. Tempo and mode of morphologic evolution near the origin of the radiolarian lineage Pterocanium prismatium. Paleobiology, 12:175-189.

MacGowran, B. 2005. Biostratigraphy. Microfossils and Geological Time. Cambridge University Press, Cambridge.

Malmgren, B.A. and Kennett, J.P. 1982. The potential of morphometrically based phylo-zonation: Application of a late Cenozoic planktonic foraminiferal lineage. Marine Micropaleontology, 7:285-296.

Malmgren, B.A. and Berggren, W.A. 1987. Evolutionary changes in some late Neogene planktonic foraminiferal lineages and their relationships to paleoceanographic changes. Paleoceanography, 2:445-456.

Malmgren, B.A., Bergren, W.A., and Lohmann, G.P. 1983. Evidence for punctuated gradualism in the late Neogene Globorotalia tumida lineage of planktonic foraminifera. Paleobiology, 9:377-389.

Miller, W. 2001. The structure of species, outcomes of speciation and the 'species problem': ideas for paleobiology. Palaeogeography, Palaeoclimatology, Palaeoecology, 176:1-10.

Norris, R.D., Corfield, R.M., and Cartlidge, J. 1996. What is gradualism? Cryptic speciation in globorotaliid foraminifera. Paleobiology, 22:386-405.

Quillévéré, F., Debat, V., and Auffray, J-C. 2002. Ontogenetic and evolutionary patterns of shape differentiation during the initial diversification of Paleocene acarinids (planktonic foraminifera). Paleobiology, 28:435-448.

Quinn, P., Thierstein, H.R., Brand, L. and Winter, A. 2003. Experimental evidence for the species character of Calcidiscus leptoporus morphotypes. Journal of Paleontology, 77:825-830.

Quinn, P.S., Sáez, A.G., Baumann, K.-H., Steel, B.A., Sprengel, C., and Medlin, L.K. 2004. Coccolithophorid biodiversity: evidence from the cosmopolitan species Calcidiscus leptoporus, p. 299-326. In Thierstein, H.R. and Young, J.R. (eds.), Coccolithophores. From Molecular Processes to Global Impact. Springer, Berlin, Heidelberg.

Reed, S. 2011. Is there an astronomer in the house? Science, 331:696-697.

Rowe, T. and Frank, L.R. 2011. The disappearing third dimension. Science, 331:712-714.

Sáez, A.G., Probert, I., Geisen, M., Quinn, P., Young, Y.R., and Medlin, L.K. 2003. Pseudo-cryptic speciation in coccolithophores. Proceedings of the National Academy of Sciences of the United States of America, 100:7163-7168.

Schmid, K. 1934. Biometrische Untersuchungen an Foraminiferen aus dem Pliozän von Ceram (Niederl.-Indien). Eclogae geologicae Helvetiae, 27(1):45-134.

Schmidt, D.N., Thierstein, H.R., and Bollmann, J. 2004. The evolutionary history of size variation of planktic foraminiferal assemblages in the Cenozoic. Palaeogeography, Palaeoclimatology, Palaeoecology, 212:159-180.

Scott, G.H. 2011. Holotypes in the taxonomy of planktonic foraminiferal morphospecies. Marine Micropaleontology, 78:96-100.

Service, R.F. 2011. Coming soon to a lab near you: Drag- and drop virtual worlds. Science, 331:669-671.

Shoval, O., Sheftel, H., Shinar, G., Hart, Y., Ramote, O., Mayo, A., Dekel, E., Kavanagh, K., and Aloh, U. 2012. Evolutionary Trade-Offs, Pareto Optimality, and the Geometry of Phenotype Space. Science, 336:1157-1160.

Tremolada, F., De Bernardi, B. and Erba, E. 2008. Size variations of the calcareous nannofossil taxon Discoaster multiradiatus (Incertae sedis) across the Paleocene-Eocene thermal maximum in ocean drilling program holes 690B and 1209B. Marine Micropaleontology, 67:239-254.

Ultsch, A. 2003. Optimal density estimation in data containing clusters of unknown structure, 15p. Technical Report No. 34, Department of Mathematics and Computer Science, University of Marburg, Germany.
www.uni-marburg.de/fb12/datenbionik/pdf/pubs/2003/ultsch03optimal.pdf

Yamasaki, M., Matsui, M., Shimada, C., Chiyonobu, S., and Sato, T. 2008. Timing of shell size increase and decrease of the planktic foraminifer Neogloboquadrina pachyderma (sinistral) during the Pleistocene, IODP Exp. 303 Site U1304, the North Atlantic Ocean. The Open Paleontology Journal, 1:18-23.

Young, J. 1990. Size variation of Neogene Reticulofenestra coccoliths from Indian Ocean DSDP cores. Journal of Micropaleontology, 9:71-86.

Young, J.R., Kucera, M., and Chung, H.W. 1996. Automated biometrics on captured light microscope images of coccoliths of Emiliania huxleyi, p. 261-277. In Moguilevsky, A. and Whatley, R. (eds.), Microfossils and Oceanic Environments. University of Wales, Aberystwyth-Press.

Young, J.R., Geisen, M., Cros, L., Kleijne, A., Sprengel, C., Probert, I., and Ostergaard, J.B. 2003. A guide to extant coccolithophore taxonomy. Journal of Nannoplankton, Special Issue, 11:1-125.