Achieving kinematic identity across shape diversity in musculoskeletal modeling
Article number: 27.1.a1
https://doi.org/10.26879/1275
Copyright Paleontological Society, January 2024
Author biographies
Plain-language and multi-lingual abstracts
PDF version
Submission: 20 February 2023. Acceptance: 17 November 2023.
ABSTRACT
Musculoskeletal modeling is emerging as a powerful approach to investigate the locomotor biomechanics of extinct taxa. These models rely on bony morphology to define joint locations and muscle geometry. Using different motion profiles to drive models of extinct and extant taxa complicates comparisons because results reflect both morphological and kinematic differences. Here we report on an approach that permits changes in shape while maintaining model kinematics.
Using a human musculoskeletal model, we carried out walking simulations of ten humans. Next, we morphed the model pelvis and proximal femur to match a reconstructed australopithecine pelvis and proximal femur. Using the kinematic results from the human walking simulations, we created new motion files based on the positions of joint centers and tracked anatomical locations. These files were used to drive simulations of the same walking trials with the australopithecine model. Joint centers and axes of the human and australopithecine models were compared for each walking trial simulation.
We found that joint centers in the australopithecine simulations were typically within ~1µm of their locations in human simulations, and joint axes differed by less than 0.005 degrees. Such small differences have negligible effects on external joint moments calculated during inverse dynamics analyses. This conservative comparison will serve as a baseline for more complex simulations. Although this work focuses on one taxon, the approach outlined is applicable to a wide variety of extinct animals.
Adam D. Sylvester. Center for Functional Anatomy and Evolution, The Johns Hopkins University School of Medicine, Baltimore, Maryland, USA. asylves4@jhmi.edu
Patricia Ann Kramer. Department of Anthropology, University of Washington, Seattle Washington, USA. pakramer@uw.edu
Keywords: hominin; biomechanics; locomotion; hip; pelvis
Final citation: Sylvester, Adam D. and Kramer, Patricia Ann. 2024. Achieving kinematic identity across shape diversity in musculoskeletal modeling. Palaeontologia Electronica, 27(1):a1.
https://doi.org/10.26879/1275
palaeo-electronica.org/content/2024/5040-modeling-extinct-locomotion
Copyright: January 2024 Paleontological Society.
This is an open access article distributed under the terms of Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0), which permits users to copy and redistribute the material in any medium or format, provided it is not used for commercial purposes and the original author and source are credited, with indications if any changes are made.
creativecommons.org/licenses/by-nc-sa/4.0/
INTRODUCTION
Locomotion is a critical adaptation for vertebrates because it provides access to key resources (i.e., food, water, safety, potential mates). Consequently, reconstructing the locomotion of extinct animals remains an important task for understanding evolutionary transitions (Nyakatura et al., 2019), reconstructing paleoecology (Thorpe, 2016), recognizing characters for phylogenetic analysis (Gatesy and Dial, 1996; Armbruster et al., 2014), and elucidating the details of a particular taxon’s locomotor behaviors (Hutchinson et al., 2005; Sellers et al., 2005). Within human evolution, perhaps no transition is as important as the evolution of bipedalism (Ward, 2002). Walking on two feet represents a fundamental shift away from more general extant primate (or even mammalian) locomotor behaviors, which employ all four limbs (e.g., terrestrial quadrupedalism, quadrumanous clambering, etc.). Despite decades of intense study, a complete understanding of early hominin bipedalism remains an elusive goal for science and thus demands continued effort (Lovejoy and Heiple 1970; Susman et al. 1984; Ruff and Higgins, 2013; DeSilva et al., 2013).
Several methodologies are used to coax the locomotor biomechanics of extinct animals from their fossilized remains, including comparative and functional morphology, the study of allometric relationships, and the analysis of fossilized footprints (see Hutchinson and Gatesy, 2006 for discussion). More recently, musculoskeletal modeling has arisen as the preeminent technique for elucidating the (internal) details of animal locomotion (Pandy, 2001; Hutchinson et al., 2005; O’Neill et al., 2013; Killen et al., 2020; Bishop et al., 2021a, 2021b, 2021c). The rise in musculoskeletal modeling is largely motivated by human health applications, and consequently human models are especially well-developed (Pedersen et al. 1997; Delp et al., 2007; Carbone et al., 2015; De Pieri et al., 2018). Musculoskeletal models are built upon linked rigid segment models and can be divided into inverse dynamic and forward dynamic simulations (Damsgaard et al., 2006). Forward dynamic simulations use muscle excitation as inputs to calculate the motion of the model. Muscle excitations can be derived from electromyography data (living animals) or estimated using dynamic optimization theory under a performance criterion (e.g., minimize energy consumption) for a particular motor task (e.g., stable walking) (Neptune 1999; Pandy, 2001; Anderson and Pandy, 2001; Crompton et al., 2012). Several authors have used this approach to reconstruct bipedal walking in australopiths, concluding that they would have used erect human-like walking and size-appropriate energy consumption (Nagano et al., 2005; Sellers et al., 2005; Crompton et al., 2012). Performance criteria are challenging to know and/or model in extant animals (Pandy, 2001) and, naturally, are more complicated for extinct ones. A potentially confounding issue in forward dynamic simulations is that model simulations that result in unique kinematics make it challenging to disentangle the effects of morphology and motion when comparing with extant taxa. That is, model simulations of extinct and extant taxa may differ both in terms of morphology but also in terms of motion profiles. As a result, it becomes complex to separate their respective effects on simulation results (e.g., muscle forces, energy consumption).
In inverse dynamic simulations, body motion and external forces (i.e., the ground reaction force) are model inputs and muscle excitations are outputs (Pedersen et al., 1997). Inverse dynamic simulations solve muscle recruitment by minimizing muscle activations (often the sum of activations raised to a power) necessary to generate required joint moments. Moments generated by muscle forces are critical because they produce the internal forces that support and move the body segments and are reflected in the external forces (i.e., the ground reaction force). Additionally, the muscle forces that create these moments require the expenditure of metabolic energy (Margaria, 1968). Wang and colleagues (2004) carried out simulations of australopithecine walking using an inverse dynamics approach, also concluding that an erect, human-like gait was likely, although one not yet adapted for long distance travel.
One potential advantage of the inverse dynamic approach for understanding extinct species is that the effect of morphology can be isolated from other sources of variability if the models are analyzed using the same kinematic and kinetic inputs. This allows the effects of morphological difference on simulation outputs to be separated from other potential sources of difference, since all simulations use the same kinematic and kinetic inputs. Such an approach does not attempt to resurrect the motion of extinct taxa de novo. Instead, this approach ultimately treats body motion and external forces as a null hypothesis that can be evaluated given known differences in morphology.
The purpose of this project was to develop and report a procedure that would allow the effects of aspects of morphological variation to be isolated from other biomechanical factors (i.e., kinematics and kinetics) by creating a common set of kinematic and kinetic data that can be used to drive models with different shapes. We focus these efforts on the evolution of the hominin hip and its role in bipedal locomotion, although our procedure could be applied to other taxa.
The hip joint and associated musculature play critical roles during human walking (and running) for propulsion, trunk stabilization, and weight-bearing (Lovejoy and Heiple 1970; Berge, 1994; Ruff, 1998; Ward, 2002; Lovejoy, 2005). While it is universally agreed that early hominins were bipeds, some researchers have argued that their pelvic and proximal femur morphology betray a less effective form of bipedalism (Stern and Susman, 1983; Susman et al. 1984; DeSilva et al., 2013). Fossils attributed to Australopithecus afarensis have figured prominently in these debates because of their antiquity and relative fossil abundance (Ward, 2002). Consequently, we have two interrelated goals. First, we want to alter (morph) an existing human musculoskeletal model to reflect australopithecine hip shape (i.e., pelvis and proximal femur). The second goal is to develop a procedure that could be used to drive simulations of models that reflect human and australopithecine hips, and that would result in identical kinematics for both models.
Here, we consider identical kinematics to mean that lower limb joint centers and axes of rotation have negligible numeric differences with respect to their positions (centers) and orientations (axes) relative to the ground reaction force (GRF). This ensures that moments about lower limb joints generated by the GRF are identical during simulations using human and australopithecine musculoskeletal models. Additionally, the morphing described below does not affect the anatomical coordinate systems of the joints. This is important because joint angles are calculated based on the coordinate systems of the joints. As a result of our requirement that joint center positions and joint axis orientations remain the same, joint angles (e.g., knee angle) for human and australopithecine musculoskeletal models will also be the same. This isolates the effects of shape from those that could arise by using different motion profiles.
This represents a different approach to the question of australopithecine pelvic morphology and locomotion from previous work, but similar in philosophy to the approach of Gatesy et al. (2009). Those authors considered a vast array of potential midstance poses for theropod dinosaurs, removing those poses that did not meet biomechanical constraints (e.g., center of mass must be above foot contact area). Driving a musculoskeletal model (MSM), that reflects the shape of the australopithecine hip, using human kinematic and kinetic inputs has the potential to reveal biomechanical constraints which make the australopithecine hip incompatible with modern human bipedalism. For future work, this would treat modern human bipedalism as the null hypothesis (because humans are the only extant bipedal hominin) and would test that null hypothesis given known differences in pelvic shape. Differences in MSM performance (e.g., muscle forces, metabolic energy consumption) may indicate features (e.g., bone strain from a finite element analysis, total energy consumption) that refute the null hypothesis (equal kinetics and kinematics) and indicate selective pressures that drove hominin hip evolution during the early evolution of Homo. Refuting hypothetical kinematics will reduce the set of potential australopithecine locomotor solutions and eventually result in a narrow range of kinematic profiles for early hominins. This more ultimate goal requires validating the method for creating the australopithecine musculoskeletal model and producing identical simulation kinematics. This validation is our proximate goal and the basis for this report.
To evaluate our procedure, we compare human and australopithecine models during walking simulations for the three-dimensional location of lower limb joint centers as well as the orientation of joint axes. We report average and maximum distances between homologous joint centers for simulations using human and australopithecine hips as well as the angle between homologous lower limb joint rotation axes.
MATERIAL AND METHODS
Walking with a Modern Human Hip
Experimental data. We utilized the existing data provided by Schreiber and Moissenet (2019), which includes motion capture (52 optical markers) and ground reaction forces for 50 participants. From the larger dataset we selected one individual to develop the protocol (detailed below) and then tested the protocol on an additional nine individuals. We used one walking trial for each participant from the self-selected walking velocity (designated C4 in Schreiber and Moissenet, 2019).
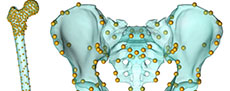
Model and human walking simulations. We adapted the ADL_Gait [beta] full body MoCap human model (Figure 1) that is part of the AnyBody modeling software for this project (AnyBody version 7.3.4). We refer to this model as the “ADL human model” and segments of the model (e.g., pelvis) use this convention (e.g., ADL human pelvis). The lower limbs of this model are based on the TLEM 2.0 validated lower limb model (Carbone et al., 2015; De Pieri et al., 2018) and altered to accommodate the data collection protocol of Schrieber and Moissenet (2019). The model is composed of upper limb, lower limb and trunk segments that are linked by frictionless joints and actuated by muscle models. The following segments comprise the lower limbs: pelvis, thigh, patella, shank, talus, and foot segments. The trunk and upper limbs include the following segments: lumbar, thorax, neck/head, arm, forearm, and hand. The joints of the lower limb allow six total degrees of freedom (three rotations at the hip and one each at the knee (flexion/extension), ankle (plantarflexion/ dorsiflexion), and subtalar (inversion/eversion) joints). Joints in the trunk and upper limb allow for trunk flexion/extension, lateral bending, rotation, as well as scapular, shoulder, and elbow movement. Forty-one lower limb muscles are composed of 169 muscle elements in each lower limb. We utilized the simple model of muscle function, which is valid for activities that require low muscle contraction velocities and operate near optimal muscle length such as walking (Fischer et al., 2018; De Pieri et al., 2018). We followed standard procedures detailed elsewhere (De Pieri et al., 2018; Sylvester et al., 2021a, 2021b) to conduct human walking simulations. This includes optimizing model dimensions and marker driver locations (termed “Parameter Identification” in the AnyBody system) and calculating model kinematics (termed “Marker Tracking”) (Figure 1). The “Parameter Identification” routine was conducted using walking trial kinematics, and this process determines the best marker driver positions and segment dimensions (e.g., length, width) to fit the marker drivers to the experimental optical markers (Lund et al., 2014). During “Marker Tracking”, the software determines the position of the model (e.g., hip angle, knee angle) that best aligns marker drivers and with the experimental optical markers.
Walking with an Australopithecine Hip
There were two major tasks to carry out simulations of modern human walking with australopithecine hip shape. The first was to alter the shape of the ADL human model to reflect the shape of the australopithecine pelvis and proximal femur. We refer to this altered model as the “ADL australopithecine model” and use this convention to refer to model segments (e.g., ADL australopithecine pelvis). The second task was to create motion data to drive simulations with the ADL australopithecine model so that it would have the same kinematics as the ADL human model walking simulations. As our goal was to model only the australopithecine hip, we maintained the positional integrity of the sacrolumbar and knee joints. We accomplish this goal by seating the trunk segments of the ADL human model on the australopithecine pelvis and by creating a hybrid femur. Details are provided below.
Capturing australopithecine hip shape. To isolate the effects of australopithecine pelvis and proximal femur, we morphed the ADL human pelvis and proximal femur to approximate the shape of the Lovejoy (1979, 1988) reconstructed A.L. 288-1 (Australopithecus afarensis; 3.2 Ma; Johanson et al., 1982; Walter, 1994) pelvis and proximal femur. Morphing the ADL human skeletal elements to the australopithecine skeletal elements maps the muscle models, including origins, paths, and insertions, to geometrically homologous positions. This morphing also maps the location of joint centers (e.g., hip joint center) but does not affect segment or joint coordinate systems (e.g., anatomical directions in the thigh), because the landmarks used to define the coordinate systems maintain relevant spatial relationships.
To begin, we surface scanned the reconstruction of the A.L. 288-1 pelvis and femur produced by Lovejoy (1979, 1988) and extracted the surface models of human pelvis and femur from the AnyBody modeling software. The first task was to reduce some of the asymmetry present in the A.L. 288-1 reconstructed pelvis (Lovejoy, 1979; Johanson et al., 1982). To accomplish this, we followed the procedure outlined by Gunz et al. (2009). First, we collected 31 landmarks (Figure 1, Appendix) on the reconstructed A.L. 288-1 pelvis. Next, we reflected and relabeled the landmarks, then aligned the two landmark sets using Procrustes superimposition, and calculated an average of the two landmark sets. Finally, we then calculated a thin plate spline (TPS) interpolation function that mapped the original landmarks to the average configuration and applied it to all the vertices of the A.L. 288-1 pelvis surface model. All further morphing processes were accomplished using the A.L. 288-1 pelvis with reduced asymmetry, and we refer to this as the “australopithecine pelvis”.
The next step was to morph the ADL human pelvis and proximal femur to reflect the shape of the australopithecine pelvis and proximal femur. This resulted in surface models that reflect the shape of the australopithecine pelvis and proximal femur, while also being topologically equivalent to the ADL pelvis and femur surface models. In this context, equivalent topology means having the same number of vertices and these vertices share the same connectivity and anatomical location. Generating models with equivalent topology facilitates morphing the ADL human model (to reflect the australopithecine shape) in the modeling software. We note that our goal was not to replicate the intricate details of a particular australopithecine pelvis and proximal femur, but to capture the features and gestalt that influence muscle mechanics in the context of the MSM.
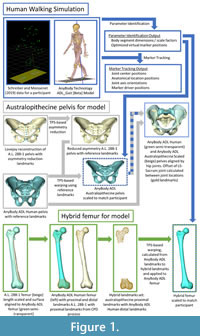
To morph the ADL human pelvis to approximate the shape of the australopithecine pelvis, we identified 63 landmarks (Appendix) on the ADL human pelvis and australopithecine pelvis. Landmark positions were collected on both pelves in Avizo (Avizo Lite 9.0), on the surface models. Both authors collected the landmarks three times over a period of three weeks on the ADL human pelvis, and intra- and interobserver errors were calculated following Corner et al. (1992) and von Cramon-Taubadel et al. (2007) and are reported in the Appendix. We then calculated the TPS interpolation function that mapped the ADL human pelvis landmarks to the australopithecine pelvis landmarks, and then applied the TPS function to the ADL human pelvis surface model vertices (i.e., morphed the ADL human pelvis; Figure 1). We refer to this morphed pelvis as the “ADL australopithecine pelvis”. The average surface distance between the final version of the ADL australopithecine pelvis and the australopithecine pelvis is ~2 mm (Figure 2). The maximum distance between surfaces is 12 mm, but these are areas located on coccyx and superior facets of the sacrum which are not critical sites of muscle origins. All morphing described above (and below for the femur) was carried out in Matlab R2021a.
We followed a similar TPS-based morphing to reflect the shape of the australopithecine proximal femur (Figure 1). To isolate the effect of the australopithecine hip from other potential effects at the knee, we created a hybrid femur that included an australopithecine proximal end combined with the original ADL human femur distal end. Our hybrid femur ensures the knees of the australopithecine and human models are identical, neither affecting the knee axis of rotation nor muscle moment arms about the knee, while allowing us to incorporate shape differences in the proximal femur which may affect hip muscle moment arms. The rest of the hybrid femur was reconstructed as a smooth TPS-based interpolation between the two ends. We began by scaling the australopithecine femur (reconstructed A.L. 288-1 femur) to have the same maximum length as the ADL human femur, and then we rigidly aligned the two femora based on the proximal 20% using an iterative closest point algorithm (Besl and McKay, 1992). Next, we evenly distributed 237 vertices (XYZ coordinates) on the proximal 20% of the ADL human femur (Moerman, 2018) and identified geometrically homologous locations on the scaled and aligned australopithecine femur using the coherent point drift algorithm (Myronenko and Song, 2010). We also identified the 2500 vertices that represent the distal end of the ADL human femur. From these three sets of vertices, we created two landmark sets. The first landmark set represented the original ADL human femur: ADL human femur proximal vertices combined with ADL human femur distal vertices. The second landmark set represented the hybrid femur: australopithecine proximal femur vertices combined with the ADL human femur distal vertices. We then calculated the TPS interpolation function that mapped the ADL human femur landmarks to those of the hybrid femur. The TPS function was then applied to the ADL human femur surface model which resulted in a femur surface model that has a proximal end shaped by australopithecine shape, a distal end which reflects the original ADL human femur, and a shaft that is a smooth, TPS-based interpolation between the two ends. For simplicity, we refer to this femur as the ADL australopithecine femur.
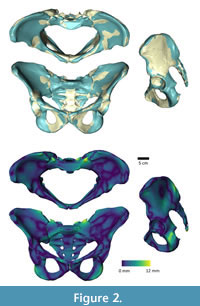
Morphing the ADL human model in AnyBody. The AnyBody modeling software can morph skeletal elements with several different functions, and we used the TPS-based morphing function which utilizes landmarks to control the morphing (as with the other TPS morphing described above). This is similar to the non-linear morphing used to transform generic musculoskeletal models to patient-specific musculoskeletal models (Marra et al., 2015; Halonen et al., 2017). Because the ADL australopithecine pelvis and femur surface models were topologically equivalent to the ADL human pelvis and femur, this only required identifying enough surface model vertices. The pelvis and femur surface models both have more than 30,000 vertices, all of which could be used to control the morphing, but at considerable computational time. Consequently, we identified 145 landmarks for the pelvis and 604 for the femur (Figure 3) for the TPS-based morphing in AnyBody. For the pelvis, this includes not only vertices from the surface model of the pelvis, but also left and right hip centers as well as the midpoint of the two anterior superior iliac spines. For the femur, 101 landmarks represent the axis of knee flexion-extension (linear interpolation between defined joint axis points), one landmark represents the center of the hip in the femoral head, while the remaining landmarks were vertices from the surface model of the bone. Appropriate AnyBody script files were written to carry out the morphing during the loading of the model in the AnyBody software. The morphed ADL model representing the australopithecine hip is shown in Figure 4.
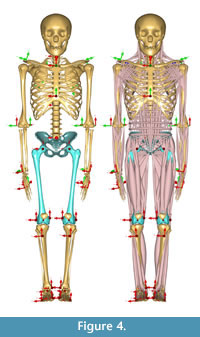To maintain the kinematics between the ADL human and ADL australopithecine models (described below), we chose to maintain joint center positions during walking simulations. For the pelvis, this means that the ADL human pelvis and ADL australopithecine pelvis needed to have the same distance between hip centers, and the same distance between hip and knee centers (femur/thigh segment). In short, the ADL australopithecine pelvis and femur used for morphing in the AnyBody software had to be sized appropriately for a particular participant from whom the kinematic data were obtained to drive the simulation. We extracted the scale factors for a participant calculated during Parameter Identification of the human simulation modeling process. We scaled the ADL australopithecine femur model using all three anatomical scaling factors (superoinferior, mediolateral, anteroposterior). We elected to scale the ADL australopithecine pelvis isometrically using the mediolateral scale factor. This created an ADL australopithecine pelvis with the desired distance between hip centers, without altering pelvic shape.
Creating kinematic drivers for the ADL australopithecine model (C3D file). Our musculoskeletal models are driven by external forces (i.e., GRFs obtained from force plates) and marker drivers. Marker drivers are coordinate locations that are rigidly attached to a model body segment (e.g., thigh, shank) and which are aligned (as closely as possible) during Marker Tracking to paired experimental optical marker positions (which are obtained through motion capture experiments). That is, for each experimental optical marker used during a walking simulation, the model must have a marker driver. The position of the marker drivers relative to experimental markers is optimized across all markers and segments to produce model kinematic patterns. The positions of the marker drivers are recorded during a walking simulation and can be extracted from simulation results.
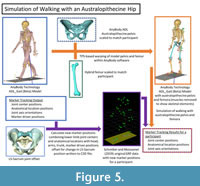In the initial human walking simulations using the ADL human model, the marker drivers were aligned to the Schreiber and Moissenet (2019) experimental optical markers during Marker Tracking. For the australopithecine simulations, we created a new set of “experimental optical markers” based on results from the human walking simulations (Figure 5). We extracted 45 positions (XYZ coordinate locations) named in the model from the human walking simulation results. For the pelvic girdle and lower limb this included the positions of the following points: sacral promontory and left and right hip centers, knee centers, ankle centers, medial and lateral femoral epicondyles, tibial tuberosities, medial malleoli, heels, and first and fifth metatarsal heads. Each segment minimally had three marker positions, which is sufficient to solve segment translation and rotation uniquely. We also used the original marker driver positions for the trunk, head, and upper limbs. We combined these positions with the original ground reaction force data and exported all data to a C3D file (Michaud and Begon, 2021). For the australopithecine simulations we created marker driver definitions that included the trunk and arms original marker drivers with new marker drivers for the lower limb and pelvic girdle. In other words, we drove the simulation with the original torso and upper body marker drivers, while the pelvis and lower limb were driven by joint centers and other critical anatomical locations. This approach ensures that the joint centers and axes are the same in each pair of simulations. We then carried out walking simulations using these data and the ADL australopithecine model and refer to these as the australopithecine walking simulations (Figure 5).
One important difference between the ADL human and ADL australopithecine pelvis, which needed to be accommodated in a new C3D file, is the position of the sacrum (Figure 1). The australopithecine pelvis is anteroposteriorly narrow relative to its mediolateral width as compared to the human condition (Tague and Lovejoy, 1986). Thus, the sacrum is in a different position relative to the hip joints in the ADL australopithecine pelvis as compared to the ADL human pelvis. This is important because the sacrum connects the trunk, head, and arms to the pelvis and lower limbs (L5-S1 joint), and sacral promontory is used to define a marker driver (i.e., defines pelvic motion). To compensate for this change, we calculated a translational offset (for each participant) between the L5-S1 joint position on the ADL human pelvis and the ADL australopithecine pelvis. These translations were between 2.8 cm and 4.4 cm in magnitude (Table 1). We then applied this offset to the markers of the arms and trunk as well as sacral points (i.e., sacral promontory) for each frame of the new C3D data, accounting for changes in pelvic position across the trial. The final C3D file, then, includes the original GRFs as well as the new “experimental optimal marker” positions (i.e., pelvic girdle/lower limb joint centers and anatomical positions combined with the sacrum-offset trunk and arm marker driver positions).
We note that creating a new set of “experimental optical marker” positions is only one possible solution to the problem described. It would also be possible to alter the joint angle files that result from the Marker Tracking protocol of the human walking simulation to accommodate the australopithecine musculoskeletal model. Initial efforts on both fronts suggested that creating the new “experimental optical marker” positions would provide a more general solution and potentially accommodate additional alternations in morphology for future investigations.
Analysis
We applied the procedure described above to one trial from each of ten participants that are part of the larger Schreiber and Moissenet (2019) experimental data. For each participant trial we conducted walking simulations using the appropriately scaled ADL australopithecine model and matching newly created C3D files. We compared lower limb joints (i.e., hip, knee, ankle, subtalar) of the ADL australopithecine walking simulation to their respective joints in the original ADL human simulation. We expect that joint centers and axes should exhibit negligible numerical differences between human and australopithecine walking simulation pairs. We consider this sufficient to establish kinematic identity.
Each joint (e.g., hip) is rigidly attached to, and numerically defined in terms of (i.e., joint center location and axes orientation), a parent (e.g., pelvis) and a child (e.g., thigh) body segment. Below, we refer to these as the “pelvis-hip” and the “thigh-hip” and other joints are similarly denoted (e.g., “thigh-knee” and “shank-knee”). Simulations express these joint positions (three Cartesian coordinate positions) and orientations (nine values describing orthonormal unit coordinate axes for the joint) in the global coordinate system of the simulation environment.
To compare joint positions across pair simulations, we calculated the Euclidean distance between homologous joint centers (e.g., right knee) for each frame within a pair of walking simulations (i.e., human to australopithecine). We report the mean and maximum distances for each pair of simulations as well as the means of those metrics across all simulations. In addition, we calculated the angle between joint axes for the hip, knee, ankle, and subtalar joints. For uniaxial axial joints (i.e., knee, ankle, subtalar), the functional axis is described by one of the three joint coordinate axes, which is the same for parent and child segments when expressed in the coordinate system of the simulation environment. The angular difference reported for this type of joint is the angle between the vectors representing homologous joint axes (e.g., angle between right knee flexion-extension axes in human and australopithecine simulations). It is important to note that the joint coordinate systems are unaffected by the morphing processes described above. Special care was taken during the morphing to include coordinate positions on the femur as landmarks that are used to define the thigh-knee coordinate axes in the model. Because the relative positions of these landmarks are not different in the human and australopithecine femur, the thigh-knee coordinate axes also do not change. Uniaxial joint angles (e.g., knee flexion-extension angle) are calculated as the angle between the thigh-knee and shank-knee coordinate systems. Following the example of the knee: the unchanged knee coordinate systems, in conjunction with the requirements that the hip, knee, and ankle centers are in identical positions and the knee functional axes are aligned when comparing human and australopithecine simulations, ensures that resulting knee joint angles will be the same in simulation pairs. The same rationale can be applied to all other uniaxial joints in the lower limb.
Because the hip has three degrees of freedom, the axes of the pelvis-hip and thigh-hip are not necessarily aligned (i.e., reflecting hip motion). We compared the hip joint axes using the pelvis-hip axes by calculating the single angle of rotation that would bring human and australopithecine hip axes into alignment. Again, we report mean and maximum angles for human-australopithecine simulation pairs, as well as the means of those metrics across simulations. Because joint angles are calculated between parent and child joint coordinate systems, if the homologous coordinate axes are in the same orientation between human and australopithecine simulation pairs, the derived joint angles will also be the same. As established above, the points used to establish thigh joint coordinates axes (including the thigh-hip) are unaffected by the morphing process. This is also true for the pelvis-hip, despite the significant change in pelvic shape. The pelvis-hip coordinate axes are based on the coordinate axes of the pelvis segment, which are established by a plane defined by the anterior superior iliac spines (ASIS) and the pubic tubercles (PT). The morphing described above does not affect this plane, only the relative positions of the points (ASIS, PT) within the plane. Thus, our requirement that joint positions and orientations being the same ensures that more traditional kinematic measures (i.e., joint angles) are also the same. Nevertheless, for one individual we plot lower limb joint angles (e.g., knee flexion-extension angle) for a pair of human and australopithecine simulations, to demonstrate that the comparisons of joint positions and orientations also ensure more traditional comparisons of joint angles. We did not compare upper limb or trunk joint positions because the changes in pelvic shape (i.e., sacral translational offset) ensured that they would be different.
RESULTS
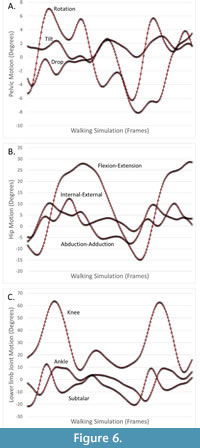Distances between human and australopithecine lower limb joint centers across all participants are provided in Table 2 and Table 3. The largest single distance between homologous joint centers in the human and australopithecine simulations is 3.89 μm (right knee for Participant 9). On average, this distance between homologous joint positions across trials was less than 1μm for both left and right lower limbs. Angles used to quantify differences in joint orientation are provided in Table 4 and Table 5. The largest angular difference across all simulations is 0.0049 degrees (hip joints for Participant 6) although most angular differences were much smaller. Of particular note is that the angular differences between human and australopithecine hip axes are identical for both the left and right sides. This is not a reflection of the reported number of digits (i.e., rounding error), but they are in fact numerically identical to the reported decimal precision (seven decimal places). Additionally, differences in the orientation of the hip axes are an order of magnitude greater than the other lower limb joints. Traditional joint angles for one pair of human and australopithecine simulations are provided in Figure 6.
DISCUSSION
The goal was to create a procedure to accommodate large shape changes in an MSM while maintaining joint center positions and joint axis orientations during simulations of locomotion. This ensures that moments about the joints generated by the GRF (which must be counteracted by muscular effort) are the same across human and australopithecine simulations of the same walking trial. The described procedure indeed creates pairs of simulations (one human, one australopithecine) that have numeric differences that are negligible with respect to joint position and orientation, while having vastly different pelvic and proximal femoral shapes. This will let us simulate human walking with both human and australopithecine shaped hips. Such simulations hold promise for detecting biomechanical parameters which may have selected against australopithecine hip morphology (i.e., the ancestral condition) in favor of subsequent derived morphologies (i.e., Homo).
In general, the differences between human and australopithecine simulations in joint center position and joint axes orientations are not the same in the left and right lower limbs. For the hip joints, however, the difference between the human and australopithecine hip axes were identical for left and right hips. These differences were also larger than the angular difference between other joint axes. The differences in left and right hips are identical because we calculated differences using the pelvis-hips, both left and right. This coordinate system is rigidly attached to the pelvis segment, and so any differences in the position of the pelvis segment will be reflected in both hip joints equally. This angular difference in hips is also larger than in the other lower limb joints. This reflects the challenges in estimating the “correct” positions for the L5-S1 joint (used to attach the trunk) and sacral promontory (used as a pelvic marker driver in the Marker Tracking analysis). We calculated a sacral offset to estimate these points in australopithecine walking simulations, but these are estimated points nonetheless. Small changes (<1um) in the position of the sacral promontory marker driver are sufficient to generate small (<0.005 degree) angular differences in pelvic orientation, which is reflected in the orientation of the hip axes. We note, however, that these angular differences (<0.005 degrees) are still negligible.
We note that as with all modeling exercises, we made specific modeling decisions that undoubtedly will affect future results (see Sylvester et al., 2021a,b; Kramer et al., 2022 for discussions of modeling choices). Perhaps the most important was the approach to the scaling of the pelvis for the ADL australopithecine model. We isometrically scaled the ADL australopithecine pelvis to maintain the distance between the hip joint centers relative to each human participant model. This choice had the advantage of maintaining the distances between the hip joint centers (as well as other lower limb joints) and the position of these joints relative to the ground reaction force. Any comparison of simulated human and australopithecine walking will be complex, but this modeling decision means that differences in muscle activations and forces can be attributed to differences in the shape of the pelvis and proximal femur. We view ours as the simplest choice which requires the fewest manipulations of the motion data. This will provide for the least complicated comparison of human and australopithecine model walking simulations, and it provides a foundation for more anatomically complex models that can include variation in kinematic patterns. Other choices would have come with different necessary adjustments to marker drivers and likely would produce different results. Additionally, we suggest that the distance between hip joint centers in humans was very likely a target of tremendous selective pressures (Washburn, 1960; Rosenberg, 1992). Thus, our scaling maintains that critical distance and scales the pelvis accordingly. Furthermore, we acknowledge that evaluating morphological variation across taxa requires including both shape (investigated methodologically here and in future extensions of this method) and size; however, we maintain that working from “simple” (shape) to “complex” (shape and size) will help separate their individual effects. Other models and simulation could address size in isolation of shape.
Finally, we also made choices with regards to the structure and function of soft tissue components. Many of these are inherent in the ADL human model (Sylvester et al., 2021b), and this includes choices regarding muscle geometry. Hip muscles in the ADL australopithecine model were generated by applying the pelvic and femoral morphing functions to the muscle geometry path points. This mapped the ADL human model muscle architecture to the ADL australopithecine pelvis and femur. This mapping is determined by the specific morphing function selected (i.e., thin plate spine) and the landmarks (e.g., anterior superior iliac spine; Appendix) used to parameterize the morphing function. Thus, the ADL australopithecine and ADL human muscle models share the same spatial relationship with the pelvic and femoral landmarks. Other choices (e.g., reconstructing australopithecine muscles de novo or basing it on chimpanzee muscle architecture; see Berge, 1994; Karakostis et al., 2021) might lead to different model results. As with all models, it may be critical to understand the sensitivity of results to these specific modeling choices. Models that are highly sensitive to input parameters will require greater caution when interpreting results than less sensitive models. Ultimately, model sensitivity must be understood in the context of the question of interest (Kramer et al., 2022).
Although this work focuses on the hominin hip, the approach and techniques outlined are applicable to a variety of extinct taxa. Application to other extinct animals would require first identifying the appropriate living model organism(s), a task that can be facilitated by leveraging phylogenetic relationships. For instance, living birds are frequently used as a model system for non-avian theropod dinosaur biology, including locomotion (Gatesy, 1990, 1991; Grossi et al., 2014; Bishop et al., 2021b, 2021c). In addition, locomotor simulation such as those demonstrated here require developing the appropriate musculoskeletal model (e.g., O’Neill et al., 2013; Bishop et al., 2021a; van Beesel et al., 2022; Cuff et al., 2022) and collecting locomotor data on living animals (e.g., Hutchinson et al., 2006). Experimental manipulation may be required to achieve the desired motion profiles (Grossi et al., 2014). While these tasks should not be considered trivial, they are achievable and could provide fruitful avenues to test hypotheses about ancient forms of locomotion.
CONCLUSIONS
Musculoskeletal modeling is increasingly being used to investigate questions of locomotor biomechanics in paleontology (Hutchinson et al., 2005; O’Neill et al., 2013; Bishop et al., 2021b). Fossilized material can be used to build the skeletal framework of a model, and muscle geometries can be reconstructed from apparent muscle origins/insertions or referencing closely related living taxa (i.e., phylogenetic bracketing; (Witmer, 1995). A significant hurdle in simulating the movement of extinct animals is selecting inputs to drive locomotor simulations. Forward dynamic models may result in unique motion profiles, making comparisons with extant taxa complex. The process demonstrated here results in two distinct models that simulate walking using identical kinematics. Given the identification of an appropriate living model organism, this technique can be leveraged to test hypotheses about the locomotor biomechanics of a wide variety of extinct taxa.
ACKNOWLEDGEMENTS
The authors wish to thank the reviewers and editors for their contributions which substantially improved this work. We also thank M.E. Lund for assistance with the AnyBody modeling system.
REFERENCES
Anderson, F.C. and Pandy, M.G. 2001. Dynamic optimization of human walking. Journal of Biomechanical Engineering, 123:381–390.
https://doi.org/10.1115/1.1392310
Armbruster, W.S., Pélabon, C., Bolstad, G.H., and Hansen, T.F. 2014. Integrated phenotypes: understanding trait covariation in plants and animals. Philosophical Transactions of the Royal Society B: Biological Sciences, 369:20130245.
https://doi.org/10.1098/rstb.2013.0245
Berge, C. 1994. How did the australopithecines walk? A biomechanical study of the hip and thigh of Australopithecus afarensis. Journal of Human Evolution, 26:259–273.
https://doi.org/10.1006/jhev.1994.1016
Besl, P.J. and McKay, N.D. 1992. A method for registration of 3-D shapes. IEEE Transactions on Pattern Analysis and Machine Intelligence, 14:239–256.
https://doi.org/10.1109/34.121791
Bishop, P.J., Cuff, A.R., and Hutchinson, J.R. 2021a. How to build a dinosaur: Musculoskeletal modeling and simulation of locomotor biomechanics in extinct animals. Paleobiology, 47:1–38.
https://doi.org/10.1017/pab.2020.46
Bishop, P.J., Falisse, A., De Groote, F., and Hutchinson, J.R. 2021b. Predictive simulations of running gait reveal a critical dynamic role for the tail in bipedal dinosaur locomotion. Science Advances, 7:eabi7348.
https://doi.org/10.1126/sciadv.abi7348
Bishop, P.J., Michel, K.B., Falisse, A., Cuff, A.R., Allen, V.R., Groote, F.D., and Hutchinson, J.R. 2021c. Computational modelling of muscle fibre operating ranges in the hindlimb of a small ground bird (Eudromia elegans), with implications for modelling locomotion in extinct species. PLoS Computational Biology, 17:e1008843.
https://doi.org/10.1371/journal.pcbi.1008843
Carbone, V., Fluit, R., Pellikaan, P., van der Krogt, M.M., Janssen, D., Damsgaard, M., Vigneron, L., Feilkas, T., Koopman, H.F.J.M., and Verdonschot, N. 2015. TLEM 2.0 - A comprehensive musculoskeletal geometry dataset for subject-specific modeling of lower extremity. Journal of Biomechanics, 48:734–741.
https://doi.org/10.1016/j.jbiomech.2014.12.034
Corner, B., Lele, S., and Richtsmeier, J. 1992. Measuring precision of three-dimensional landmark data. Journal of Quantitative Anthropology 3:347–359.
Crompton, R.H., Pataky, T.C., Savage, R., D’Août, K., Bennett, M.R., Day, M.H., Bates, K., Morse, S., and Sellers, W.I. 2012. Human-like external function of the foot, and fully upright gait, confirmed in the 3.66 million year old Laetoli hominin footprints by topographic statistics, experimental footprint-formation and computer simulation. Journal of The Royal Society Interface, 9:707–719.
https://doi.org/10.1098/rsif.2011.0258
Cuff, A.R., Demuth, O.E., Michel, K., Otero, A., Pintore, R., Polet, D.T., Wiseman, A.L.A., and Hutchinson, J.R. 2022. Walking–and running and jumping–with dinosaurs and their cousins, viewed through the lens of evolutionary biomechanics. Integrative and Comparative Biology, 62:1281–1305.
https://doi.org/10.1093/icb/icac049
Damsgaard, M., Rasmussen, J., Christensen, S.T., Surma, E., and de Zee, M. 2006. Analysis of musculoskeletal systems in the AnyBody Modeling System. Simulation Modelling Practice and Theory, 14:1100–1111. https://doi.org/10.1016/j.simpat.2006.09.001
Delp, S.L., Anderson, F.C., Arnold, A.S., Loan, P., Habib, A., John, C.T., Guendelman, E., and Thelen, D.G. 2007. OpenSim: open-source software to create and analyze dynamic simulations of movement. IEEE Transactions on Biomedical Engineering, 54:1940–1950.
https://doi.org/10.1109/TBME.2007.901024
De Pieri, E., Lund, M.E., Gopalakrishnan, A., Rasmussen, K.P., Lunn, D.E., and Ferguson, S.J. 2018. Refining muscle geometry and wrapping in the TLEM 2 model for improved hip contact force prediction. PLoS ONE, 13:e0204109.
https://doi.org/10.1371/journal.pone.0204109
DeSilva, J.M., Holt, K.G., Churchill, S.E., Carlson, K.J., Walker, C.S., Zipfel, B., and Berger, L.R. 2013. The lower limb and mechanics of walking in Australopithecus sediba. Science, 340:1232999.
https://doi.org/10.1126/science.1232999
Fischer, M.C.M., Eschweiler, J., Schick, F., Asseln, M., Damm, P., and Radermacher, K. 2018. Patient-specific musculoskeletal modeling of the hip joint for preoperative planning of total hip arthroplasty: A validation study based on in vivo measurements. PLoS ONE, 13:e0195376.
https://doi.org/10.1371/journal.pone.0195376
Gatesy, S.M. 1990. Caudofemoral musculature and the evolution of theropod locomotion. Paleobiology, 16:170–186.
https://doi.org/10.1017/S0094837300009866
Gatesy, S.M. 1991. Hind limb scaling in birds and other theropods: Implications for terrestrial locomotion. Journal of Morphology, 209:83–96.
https://doi.org/10.1002/jmor.1052090107
Gatesy, S.M. and Dial, K.P. 1996. Locomotor modules and the evolution of avian flight. Evolution, 50:331–340.
https://doi.org/10.1111/j.1558-5646.1996.tb04496.x
Gatesy, S.M., Bäker, M., and Hutchinson, J.R. 2009. Constraint-based exclusion of limb poses for reconstructing theropod dinosaur locomotion. Journal of Vertebrate Paleontology, 29:535–544.
https://doi.org/10.1671/039.029.0213
Grossi, B., Iriarte-Díaz, J., Larach, O., Canals, M., and Vásquez, R.A. 2014. Walking like dinosaurs: chickens with artificial tails provide clues about non-avian theropod locomotion. PLoS ONE, 9:e88458. https://doi.org/10.1371/journal.pone.0088458
Gunz, P., Mitteroecker, P., Neubauer, S., Weber, G.W., and Bookstein, F.L. 2009. Principles for the virtual reconstruction of hominin crania. Journal of Human Evolution, 57:48–62.
https://doi.org/10.1016/j.jhevol.2009.04.004
Halonen, K.S., Dzialo, C.M., Mannisi, M., Venäläinen, M.S., de Zee, M., and Andersen, M.S. 2017. Workflow assessing the effect of gait alterations on stresses in the medial tibial cartilage - combined musculoskeletal modelling and finite element analysis. Scientific Reports, 7:17396.
https://doi.org/10.1038/s41598-017-17228-x
Hutchinson, J.R., Anderson, F.C., Blemker, S.S., and Delp, S.L. 2005. Analysis of hindlimb muscle moment arms in Tyrannosaurus rex using a three-dimensional musculoskeletal computer model: implications for stance, gait, and speed. Paleobiology, 31:676–701.
https://doi.org/10.1666/0094-8373(2005)031[0676:AOHMMA]2.0.CO;2
Hutchinson, J.R. and Gatesy, S.M. 2006. Beyond the bones. Nature, 440:292–294.
https://doi.org/10.1038/440292a
Hutchinson, J.R., Schwerda, D., Famini, D.J., Dale, R.H.I., Fischer, M.S., and Kram, R. 2006. The locomotor kinematics of Asian and African elephants: changes with speed and size. Journal of Experimental Biology, 209:3812–3827.
https://doi.org/10.1242/jeb.02443
Johanson, D.C., Lovejoy, C.O., Kimbel, W.H., White, T.D., Ward, S.C., Bush, M.E., Latimer, B.M., and Coppens, Y. 1982. Morphology of the Pliocene partial hominid skeleton (A.L. 288-1) from the Hadar formation, Ethiopia. American Journal of Physical Anthropology, 57:403–451.
https://doi.org/10.1002/ajpa.1330570403
Karakostis, F.A., Haeufle, D., Anastopoulou, I., Moraitis, K., Hotz, G., Tourloukis, V., and Harvati, K. 2021. Biomechanics of the human thumb and the evolution of dexterity. Current biology, 31:1317–1325.
https://doi.org/10.1016/j.cub.2020.12.041
Killen, B.A., Falisse, A., De Groote, F., and Jonkers, I. 2020. In silico-enhanced treatment and rehabilitation planning for patients with musculoskeletal disorders: Can musculoskeletal modelling and dynamic simulations really impact current clinical practice? Applied Sciences, 10:7255.
https://doi.org/10.3390/app10207255
Kramer, P.A., Feuerriegel, E.M., Lautzenheiser, S.G., and Sylvester, A.D. 2022. Sensitivity of musculoskeletal models to variation in muscle architecture parameters. Evolutionary Human Sciences 4:e6.
https://doi.org/10.1017/ehs.2022.6
Lovejoy, C. O. 1979. A reconstruction of the pelvis of AL-288-1 (Hadar Formation, Ethiopia). American Journal of Physical Anthropology, 50, 413.
Lovejoy, C.O. 1988. Evolution of human walking. Scientific American, 259:118–125.
Lovejoy, C.O. 2005. The natural history of human gait and posture: Part 1. Spine and pelvis. Gait & Posture, 21:95–112.
https://doi.org/10.1016/j.gaitpost.2004.01.001
Lovejoy, C.O. and Heiple, K.G. 1970. A reconstruction of the femur of Australopithecus africanus. American Journal of Physical Anthropology, 32:33–40.
https://doi.org/10.1002/ajpa.1330320105
Lund, M.E., Andersen, M.S., de Zee, M., and Rasmussen, J. 2015. Scaling of musculoskeletal models from static and dynamic trials. International Biomechanics, 2:1–11.
https://doi.org/10.1080/23335432.2014.993706
Margaria, R. 1968. Positive and negative work performances and their efficiencies in human locomotion. Internationale Zeitschrift für angewandte Physiologie einschließlich Arbeitsphysiologie, 25:339–351. https://doi.org/10.1007/BF00699624
Marra, M.A., Vanheule, V., Fluit, R., Koopman, B.H.F.J.M., Rasmussen, J., Verdonschot, N., and Andersen, M.S. 2015. A subject-specific musculoskeletal modeling framework to predict in vivo mechanics of total knee arthroplasty. Journal of Biomechanical Engineering, 137: 020904.
https://doi.org/10.1115/1.4029258
Michaud, B. and Begon, M. 2021. ezc3d: An easy C3D file I/O cross-platform solution for C++, Python and MATLAB. Journal of Open Source Software, 6:2911.
https://doi.org/10.21105/joss.02911
Moerman, K.M. 2018. GIBBON: The geometry and image-based bioengineering add-on. Journal of Open Source Software, 3:506.
https://doi.org/10.21105/joss.00506
Myronenko, A. and Song, X. 2010. Point set registration: coherent point drift. IEEE Transactions on Pattern Analysis and Machine Intelligence, 32:2262–2275.
https://doi.org/10.1109/TPAMI.2010.46
Nagano, A., Umberger, B.R., Marzke, M.W., and Gerritsen, K.G.M. 2005. Neuromusculoskeletal computer modeling and simulation of upright, straight-legged, bipedal locomotion of Australopithecus afarensis (A.L. 288-1). American Journal of Physical Anthropology, 126:2–13.
https://doi.org/10.1002/ajpa.10408
Neptune, R.R. 1999. Optimization algorithm performance in determining optimal controls in human movement analyses. Journal of Biomechanical Engineering, 121:249–252.
https://doi.org/10.1115/1.2835111
Nyakatura, J.A., Melo, K., Horvat, T., Karakasiliotis, K., Allen, V.R., Andikfar, A., Andrada, E., Arnold, P., Lauströer, J., Hutchinson, J.R., Fischer, M.S., and Ijspeert, A.J. 2019. Reverse-engineering the locomotion of a stem amniote. Nature, 565:351–355.
https://doi.org/10.1038/s41586-018-0851-2
O’Neill, M.C., Lee, L.-F., Larson, S.G., Demes, B., Stern, J.T., and Umberger, B.R. 2013. A three-dimensional musculoskeletal model of the chimpanzee (Pan troglodytes) pelvis and hind limb. Journal of Experimental Biology, 216:3709–3723.
https://doi.org/10.1242/jeb.079665
Pandy, M.G. 2001. Computer modeling and simulation of human movement. Annual Review of Biomedical Engineering, 3:245–273.
https://doi.org/10.1146/annurev.bioeng.3.1.245
Pedersen, D.R., Brand, R.A., and Davy, D.T. 1997. Pelvic muscle and acetabular contact forces during gait. Journal of Biomechanics, 30:959–965.
https://doi.org/10.1016/S0021-9290(97)00041-9
Rosenberg, K.R. 1992. The evolution of modern human childbirth. American Journal of Physical Anthropology, 35:89–124.
https://doi.org/10.1002/ajpa.1330350605
Ruff, C. 1998. Evolution of the Hominid Hip, p. 449–469. In Strasser, E., Fleagle, J.G., Rosenberger, A.L., and McHenry, H.M. (eds.), Primate Locomotion. Springer US.
https://doi.org/10.1007/978-1-4899-0092-0_23
Ruff, C.B. and Higgins, R. 2013. Femoral neck structure and function in early hominins. American Journal of Physical Anthropology, 150:512–525.
https://doi.org/10.1002/ajpa.22214
Schreiber, C. and Moissenet, F. 2019. A multimodal dataset of human gait at different walking speeds established on injury-free adult participants. Scientific Data, 6:111.
https://doi.org/10.1038/s41597-019-0124-4
Sellers, W.I., Cain, G.M., Wang, W., and Crompton, R.H. 2005. Stride lengths, speed and energy costs in walking of Australopithecus afarensis: using evolutionary robotics to predict locomotion of early human ancestors. Journal of The Royal Society Interface, 2:431–441.
https://doi.org/10.1098/rsif.2005.0060
Stern, J.T. and Susman, R.L. 1983. The locomotor anatomy of Australopithecus afarensis. American Journal of Physical Anthropology, 60:279–317.
https://doi.org/10.1002/ajpa.1330600302
Susman, R.L., Stern, J.T., and Jungers, W.L. 1984. Arboreality and bipedality in the Hadar hominids. Folia Primatologica, 43:113–156.
https://doi.org/10.1159/000156176
Sylvester, A.D., Lautzenheiser, S.G., and Kramer, P.A. 2021a. Muscle forces and the demands of human walking. Biology Open, 10:bio058595.
https://doi.org/10.1242/bio.058595
Sylvester, A.D., Lautzenheiser, S.G., and Kramer, P.A. 2021b. A review of musculoskeletal modelling of human locomotion. Interface Focus, 11:20200060. Royal Society.
https://doi.org/10.1098/rsfs.2020.0060
Tague, R.G. and Lovejoy, C.O. 1986. The obstetric pelvis of A.L. 288-1 (Lucy). Journal of Human Evolution, 15:237–255. https://doi.org/10.1016/S0047-2484(86)80052-5
Thorpe, S.K.S. 2016. Symposium on primate ecomorphology: Introduction. Journal of Anatomy, 228:531–533.
https://doi.org/10.1111/joa.12455
van Beesel, J., Hutchinson, J.R., Hublin, J.-J., and Melillo, S. 2022. Comparison of the arm-lowering performance between Gorilla and Homo through musculoskeletal modeling. American Journal of Biological Anthropology, 178:399–416.
https://doi.org/10.1002/ajpa.24511
von Cramon-Taubadel, N., Frazier, B.C., and Lahr, M.M. 2007. The problem of assessing landmark error in geometric morphometrics: Theory, methods, and modifications. American Journal of Physical Anthropology 134:24–35.
https://doi.org/10.1002/ajpa.20616
Walter, R.C. 1994. Age of Lucy and the First Family: Single-crystal 40Ar/39Ar dating of the Denen Dora and lower Kada Hadar members of the Hadar Formation, Ethiopia. Geology, 22:6–10.
https://doi.org/10.1130/0091-7613(1994)022<0006:AOLATF>2.3.CO;2
Wang, W., Crompton, R.H., Carey, T.S., Günther, M.M., Li, Y., Savage, R., and Sellers, W.I. 2004. Comparison of inverse-dynamics musculo-skeletal models of AL 288-1 Australopithecus afarensis and KNM-WT 15000 Homo ergaster to modern humans, with implications for the evolution of bipedalism. Journal of Human Evolution, 47:453–478.
https://doi.org/10.1016/j.jhevol.2004.08.007
Ward, C.V. 2002. Interpreting the posture and locomotion of Australopithecus afarensis: Where do we stand? American Journal of Physical Anthropology, 119:185–215.
https://doi.org/10.1002/ajpa.10185
Washburn, S.L. 1960. Tools and human evolution. Scientific American, 203:63–75.
Witmer, L. 1995. The extant phylogenetic bracket and the importance of reconstructing soft tissues in fossils, p. 19–33. In Thomason, J.J. (ed.), Functional morphology in vertebrate paleontology. Cambridge University Press, New York.
