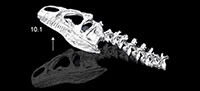
Multibody dynamics model of head and neck function in Allosaurus (Dinosauria, Theropoda)
Article number: 16.2.11A
https://doi.org/10.26879/338
Copyright Palaeontological Association, May 2013
Author biographies
Plain-language and multi-lingual abstracts
PDF version
Submission: 18 July 2012. Acceptance: 21 January 2013
{flike id=389}
ABSTRACT
We present a multibody dynamics model of the feeding apparatus of the large Jurassic theropod dinosaur Allosaurus that enables testing of hypotheses about the animal's feeding behavior and about how anatomical parameters influence function. We created CT- and anatomical-inference-based models of bone, soft tissue, and air spaces which we use to provide inertial properties for musculoskeletal dynamics. Estimates of bone density have a surprisingly large effect on head inertial properties, and trachea diameter strongly affects moments of inertia of neck segments for dorsoventral movements. The ventrally-placed insertion of m. longissimus capitis superficialis in Allosaurus imparted over twice the ventroflexive accelerations of a proxy control insertion lateral to the occipital condyle, the latter being its position in nearly all other theropods. A feeding style that involved defleshing a carcass by avian-raptor-like retraction of the head in Allosaurus is more probable than is lateroflexive shake-feeding, such as that seen in crocodilians and inferred for tyrannosaurids.
Eric Snively. Department of Mechanical Engineering, Russ College of Engineering, 249 Stocker Center, Ohio University, Athens, OH 45701, USA
John R. Cotton. Department of Mechanical Engineering, Russ College of Engineering, 249 Stocker Center, Ohio University, Athens, OH 45701, USA
Ryan Ridgely. Department of Biomedical Sciences, Heritage College of Osteopathic Medicine, Ohio University, Athens, OH 45701, USA
Lawrence M. Witmer. Department of Biomedical Sciences, Heritage College of Osteopathic Medicine, Ohio University, Athens, OH 45701, USA
Keywords: Dinosauria; biomechanics; feeding; multibody dynamics; muscle
Final citation: Snively, Eric, Cotton, John R., Ridgely, Ryan, and Witmer, Lawrence M. 2013. Multibody dynamics model of head and neck function in Allosaurus (Dinosauria, Theropoda), Palaeontologia Electronica Vol. 16, Issue 2; 11A 29p. https://doi.org/10.26879/338
palaeo-electronica.org/content/2013/389-allosaurus-feeding
INTRODUCTION
Allosaurus Musculoskeletal Anatomy
Allosaurus was the most common dinosaurian predator in its ecosystems during the Late Jurassic of North America (154–148 Ma; Foster, 2007). There are at least two species of Allosaurus (Chure, 2000; Loewen, 2009). These and other taxa in Allosauroidea had ball-and-socket joints between their opisthocoelous vertebral centra (Madsen, 1976; Holtz et al., 2004; Brusatte and Sereno, 2007), suggesting a highly mobile neck. This morphology contrasts with tyrannosaurid theropods of similar size to allosauroids, such as Tyrannosaurus rex, in which the centra have amphiplatyan (flat) intervertebral joints (Brochu, 2003). Allosaurus crania have ventrolaterally sweeping paroccipital processes, with unusual muscle attachments that suggest powerful ventroflexion of the head (Bakker, 1998[2000]; Rayfield et al., 2001; Snively and Russell, 2007a; Carrano et al., 2012). Computer modeling of range of motion and musculoskeletal dynamics enables testing of hypotheses related to Allosaurus feeding, and will guide more elaborate investigations of anatomy and feeding in this apex predator.
Multibody Dynamics of Head and Neck Motion
Dynamics of head and neck motion have precedent in studies of humans and other extant animals. Dynamic simulations of head and neck function in humans (Delp and Loan, 1995; Vasavada et al., 1998, 2008a, b; van Lopik and Acar, 2007; Marin et al., 2010) enable non-invasive, exploratory analyses with precise control over input variables. Analogous benefits apply to simulations of extinct animals, for which in vivo study is impossible and most parameter values are unknown. Non-human models of head-neck function have concentrated on feeding in reptiles. For example, Moazen et al. (2008a) simulated dynamics of biting in the lizard Uromastix, incorporating complex aspects of muscle force production, and validation with experimental data, as inputs for finite element analysis of bite stress. Curtis et al. (2010a,b) constructed a model of the tuatara Sphenodon (including neck muscles) to examine the effects of muscle activation levels on bite force and neuromuscular control. Modeled bite forces were lower than the forces that the tuataras exerted experimentally (Curtis et al., 2010b). Moazen, Curtis, and colleagues used the software MSC Adams (MSC Software, Santa Ana, California, USA; see Appendix 1) for their simulations.
Bates and Falkingham (2012) bridged extant and fossil dynamics with simulations of biting in humans, Alligator, Tyrannosaurus, and Allosaurus. Their dynamic simulations found higher bite forces in Allosaurus than expected from previous static analyses based on finite element reaction forces (Rayfield et al., 2001). Bates and Falkingham's (2012) analyses showed the versatility of multibody dynamics methods, adapting the free program GaitSym which is normally applied to simulate locomotion (Sellers et al., 2009; http://www.animalsimulation.org).
Feeding Apparatus Dynamics of Allosaurus: Goals and Hypotheses
Using multibody dynamics, we can simulate head and neck motions in Allosaurus with ranges of parameter values, enabling us to estimate inertial properties and accelerations of its head and neck and circumscribe possible feeding behavior. There are three potential benefits to this approach. First, we can quantify the functional morphology behind the ecological success of a widespread and long-lasting carnivorous taxon. Second, lessons from constructing the multibody dynamics model will establish its effectiveness and methods of best use for comparative studies of other taxa, including large Morrison theropods such as Ceratosaurus that partitioned predatory niches with Allosaurus (Foster, 2007). Finally, we can address explicit hypotheses about neck function that are difficult to test by other means.
Neck muscles of large theropods varied in morphology, relative size, and functional capability. Snively and Russell (2007a) presented measurement and statistical evidence that Allosaurus had smaller dorsiflexors than adult tyrannosaurids of equivalent size. Conversely, Snively (2006) established morphometrically that allosauroids had larger ventroflexive moment arms than did tyrannosaurids, and that Allosaurus's insertion of m. longissimus capitis superficialis may have further increased ventroflexive torque. The effect of this insertion on ventroflexive angular accelerations has yet to be quantified.
By comparing angular accelerations, we test the hypothesis that unusual muscle attachments below the level of the occipital condyle of Allosaurus conferred more rapid ventroflexion than if the muscle inserted in the same coronal plane as the condyle. Such a lateral insertion is present in nearly all other theropods. Misplacing it here in Allosaurus serves as a control, enabling us to compare ventroflexive accelerations in the "real" morphology and a proxy basal condition. Greater ventroflexive acceleration would have behavioral consequences for Allosaurus, perhaps enabling rapid downward strikes (Bakker, 1998[2000]; Rayfield et al., 2001) and augmented bite force by slower motions (Antón et al., 2003), compared with ecological contemporaries such as Torvosaurus and Ceratosaurus (Foster, 2007).
MATERIALS AND METHODS
Bone and Soft Tissue Geometry
The Allosaurus skull specimen used is a cast of Museum of the Rockies (MOR) 693, scanned at a slice thickness of 300 µm on a Toshiba Aquilion 64 computed tomographic (CT) scanner at O'Bleness Memorial Hospital (Athens, Ohio). Chure (2000), Loewen (2009), and Chure and Loewen (unpublished data) have reviewed the specimen's species taxonomy. Here we defer to upcoming publications by these authors and refer to the animal simply as Allosaurus, omitting the species designation.To calculate mass, centers of mass (COM), and mass moments of inertia (I), the head and neck geometries of Allosaurus (including major air spaces) were modeled in Solid Edge (Siemens PLM, Köln, Germany) as a series of lofted elliptical frusta. For non-elliptical cross sections, we derived equations to obtain I for any super-elliptical frusta (Appendix 2) with the same radii as the Solid Edge lofts.
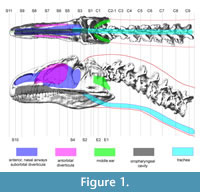
We used CT-based reconstructions of the cervical vertebrae and skull of MOR 693 (Figure 1) to obtain dimensions and anteroposterior position of each cross section. Dorsal- and lateral-view soft-tissue outlines (Figure 1) were reconstructed based on the CT-based bone geometry and muscle and other soft-tissue inferences (Tsuihiji, 2005, 2007, 2010; Snively, 2006; Snively and Russell (2007a, b). The skull is taphonomically sheared and crushed transversely, but modeling it symmetrical in dorsal view brought its width closer to that of Loewen's undistorted reconstruction of the skull (figure 2.4 in Loewen, 2009). Dorsal and lateral outlines were traced in Adobe Illustrator and scaled to the lengths of the original specimen. Lines transecting both views at anteroposteriorly equivalent points (Figure 1) guided collection of coordinates in the program Plot Digitizer (plotdigitizer.sourceforge.net/) at longitudinal (x), vertical (y), and transverse (z) positions (Henderson, 1999). The x-y coordinate origin of the drawings was placed at the posterior ventral point of the segment containing cervical vertebra C9, which became the origin point for positioning ellipses in Solid Edge.
The cranium of Allosaurus extends posterolaterally beyond the occipital condyle. The anterior neck segment was therefore modeled as a frustum wedged between these wings of the occiput and lower jaws. The skull was modeled with a lofted cutout posteriorly, forming the inverse shape of the frustum. This simplified reconstruction facilitated the modeling process, but does not capture the posteroventral slope of the occipital region or the width of neck muscles inserting dorsally onto the parietals (which are wider than the occipital condyle). However, these regions were continuous in life, and the method replicates their collective mass and I necessary for calculating dynamic outcomes.
Trachea and Air Space Geometry
The same geometric slicing methods (Henderson, 1999) served for reconstructing air spaces and other internal features. The esophagus is enormously distensible, but in tetrapods generally it is a collapsed potential space along much of its length. Our models treated the esophagus as empty and collapsed for calculating I. The trachea lies adjacent to the esophagus, ventral to the prevertebral space and muscles, between the prevertebral and pretracheal fasciae. In birds the trachea is loosely anchored to the vertebral column within these fasciae, and its position shifts as the bird turns its neck. However, once exiting the pharynx, the trachea is fairly close to the ventral edge of the neck in both birds and crocodilians, and deviates from the midline in birds only at the transition between cervical and dorsal vertebrae, often entering the thoracic cavity lateral to the vertebrae and posterolateral neck muscles (Snively, 2006).
The trachea was modeled with two respective diameters to account for unknown scaling relationships and to examine sensitivity of inertial properties to estimates of tracheal size. Hinds and Calder (1971) derived an equation for birds relating average tracheal diameter dtrachea to body mass m.
1) dtrachea = 0.531m^0.348
These authors excluded ostriches from their sample, because they lacked body mass or all tracheal dimensions from their ostrich samples. However, applying Equation 1 to ostriches of known m and dtrachea yields average dtrachea within +11/-2% of the actual values (Fowler, 1991). By Equation 1, dtrachea for this Allosaurus (with a best estimate m of 1500.91 kg: Bates et al., 2009) is 6.78 cm. Birds have proportionally longer necks than did Allosaurus, and the mass of Allosaurus is one to four orders of magnitude greater than any bird in Hinds and Calder's (1971) sample. We therefore derived regression Equation 2 from their data on relatively short-necked galliform birds (Hinds and Calder, 1971).
2) dtrachea = 0.2959log m – 0.3406
This regression resulted in dtrachea of 4.0 cm for Allosaurus, which is a tentative estimate given the low sample size from Hinds and Calder (1971) and other uncertainties.
Transect lines crossed landmarks associated with major air spaces in the head (Figure 1), including the ventral edge of the trachea. For the oral cavity and oropharynx, landmarks included the anterior and ventral edges of the palate, the choanae, and approximate relative positions of the glottis and dorsal surface of the tongue, based on comparisons to dissected archosaurs (Snively, 2006). The nasal airway, olfactory region, and suborbital sinus were modeled as one space, because the extents of soft tissues (including conchae) are unknown. Witmer (1997), Witmer and Ridgely (2008), and Dufeau (2011) described bony correlates and soft-tissue constraints for antorbital and middle ear sinuses (Figure 1).
Tissue Densities
Without data on pneumatic spaces within the neck of Allosaurus, an average density of 1060 kg/m^3 (that of skeletal muscle: Witmer and Ridgely, 2008) was assigned to all tissues of the neck segments. The combination of substantial neck musculature (Snively and Russell, 2007a; Bates et al., 2009), dense bone, vasculature, and vertebral air spaces would presumably converge towards this density value. Samman (2006; in press) has established that vertebral centra of tyrannosaurs have ostrich-like camellate pneumaticity (with many small chambers: Britt, 1993). Allosaurus generally resembled these large theropods in pneumaticity of the vertebral centra (O'Connor, 2006; Benson et al., 2012). However, sizes of pneumatic diverticula (epithelial air-filled sacs lateral to and within the centra) are unknown for Allosaurus and vary along the necks of individual anseriform birds (O'Connor, 2004). A neck tissue density of 1060 kg/m^3 for Allosaurus may be conservatively high (Wedel, 2005; Bates et al., 2009), although the modeled trachea reduces the overall density of neck segments.
Unlike the neck, the skull of Allosaurus is a more open structure with clear indication of bone- versus air-space volume. To estimate density, mass, center of mass, and I of the entire head, we incorporated bone volume and density, head volume (including and excluding air spaces), and soft-tissue density. Avizo calculated the volume of bone from segmented CT geometry. The CT dataset is missing the right lower jaw, but the left mandible is present. We segmented the left mandible and, assuming bilateral symmetry, added its volume to the total. We subtracted the volume of hollow air space within the nasals, based on the specimen's dimensions and cross-sectional data from CT scans of other Allosaurus nasals (Snively et al., 2006).Overall head volume, with and without air spaces, was taken from the Solid Edge reconstructions.
Density of head soft tissues ρST was set at 1050 kg/m^3 (Witmer and Ridgely, 2008). The skull was assumed to be predominately but not exclusively compact bone (Snively et al., 2006; also in tyrannosaurs: Brochu, 2003, Shychoski unpublished data). Bone densities ρB were varied parametrically based on data from Witmer and Ridgely (2008) and Dumont (2010). Witmer and Ridgely (2008) calculated a mean of 1350 kg/m^3 for skull bone of crocodilians and mammals, which is realistic for a combination of compact and cancellous bone. Birds have high ρB from 2100 to 2300 kg/m^3 (Dumont, 2010), which maintains high stiffness at low mass. Birds are the closest living relatives of Allosaurus, but the large theropod lacks flight constraints on skull mass. A ρB of 1750 kg/m^3 (Dumont, 2010) may be realistic for the skull's compact bone (Cowin, 2001), although cancellous bone would bring the overall density down. Bone densities of greater than 1350 kg/m^3 (Witmer and Ridgely, 2008) probably represent overestimates, and will contribute to conservatively low estimates of head accelerations.
With estimates of ρST and ρB, it was possible to calculate an overall tissue density, ρtissue,, for the volume of the head not taken up by air spaces. This combination of densities will not affect estimates of head mass, but will be less accurate for I and COM because bone and soft tissue are not consistently distributed throughout the head. Ideally we would model full bone and soft-tissue reconstructions for Allosaurus, with validation through MRI and CT segmentation modeling of all head tissues of extant archosaurs. For now, we feel assigning a uniformly distributed average ρtissue, is an adequate approximation, because head tissues were distributed about the centralized airways and antorbital diverticula. The head tissues of Allosaurus had concentrations of high densities anteriorly (tooth-bearing bones) and posteriorly (braincase and jaw muscles), and dorsal bone of the skull roof offset with a greater volume of soft tissues ventrally. No model can capture this balance of masses with perfect accuracy. However, assigning uniform tissue densities probably yields coordinates of the COM (and I about it) close to realistic values, subject to testing by future detailed modeling and validation studies.
We can estimate anatomically realistic ranges of ρtissue by combining relative volumes and absolute densities (ρB and ρST) of bone and soft tissues. We calculated volume fractions of bone and soft tissue (BVF and SVF) by subtracting Avizo-calculated bone volume from overall head volume; SVF was the volume remaining. Bone and soft tissue volume fractions (the volume of the head that does include air spaces) add up to one for all tissue in the head. The tissue density was then found by the rule of mixtures
3) ρtissue = ρB X BVF + ρST X SVF
Masses, Centers of Mass, Mass Moments of Inertia
We used Solid Edge to calculate mass, center of mass, and I of the neck segments, based on external geometry and the two tracheal models, and applied equations in Appendix 2 to calculate values for non-elliptical cross sections. Orientation of the Allosaurus model varied in Solid Edge and Adams relative to their global coordinate systems. We rotated local coordinate systems at segment centers of mass in Solid Edge to match the global system in Adams to ensure that I would be about equivalent axes in the two programs. Calculations for the head incorporated all variants of bone density (Witmer and Ridgely, 2008; Dumont, 2010), as well as models with and without air spaces. A head model without air spaces is unrealistic, but a solid model is informative for comparing dynamic results between easily-constructed models versus anatomically intensive models that include air spaces and bone densities.
The Adams model consisted of CT-based bone geometry for attaching muscles and visualizing range of motion, and inertial properties of the Solid Edge reconstructions were applied to the bones. The head center of mass was within the envelope of the Solid Edge model, but outside the bone of the CT-based Adams model (occupying a point equidistant between the lacrimal bones). Adams requires that center of mass be placed on or within the surface of a geometry, and centers of mass were therefore placed at a point associated with a sphere added to the skull's geometry.
Muscle Geometry, Cross-sectional Area, and Force
Muscle attachments and reconstructions were based on data in Snively and Russell (2007a,c) and Tsuihiji (2005, 2007, 2010). Forces were estimated only for those muscles with unambiguous origins and insertions (Snively and Russell, 2007a, c; Tsuihiji, 2005, 2007, 2010), including m. longissimus capitis superficialis. Muscles with more ambiguous attachments, including m. complexus and the parts of m. splenius capitis, were not incorporated into the simulations. These muscles were not involved in ventroflexion (Snively, 2012) and not relevant to testing our hypothesis.
Muscle action was modeled assuming constant force. Future models will incorporate spring-damper qualities of muscles with force varying with length and velocity (Gordon et al., 1966; Otten, 1987; van Ruijven and Weijs, 1990; Westneat, 2003; Curtis et al., 2008, 2010 a, b; Moazen et al., 2008a, b; Domire and Challis, 2010; Winters et al., 2011; Bates and Falkingham, 2012; Miller et al., 2012). A muscle's maximum force Fmaxat a given length or velocity is proportional to its cross-sectional area. We estimated muscle cross-sectional areas using the methods of Snively and Russell (2007b): radii of reconstructed muscles are measured from scaled lateral and dorsal (or ventral) drawings, and area is then calculated assuming a superelliptical cross section with an exponent of 2.5 (Snively and Russell, 2007b). Areas were calculated for baseline and robust (+10% in radius dimensions) reconstructions.
To obtain a baseline force for the muscles, we multiplied these areas by a specific tension (ST) of muscle. Specific tension varies widely between studies. Curtis et al. (2010b) determined an isometric ST for reptile muscle of 82.5 N/cm^2, and cited still higher values. Isometric ST can be 1.5 times greater than concentric (shortening) force (Snively and Russell 2007b). We therefore applied a value of 55 N/cm^2 as a baseline concentric ST of Allosaurus neck muscles. We chose this ST because it derives from experimental results for reptile muscle, but it is at the higher end of the range reported for vertebrate muscle (usually between 20-30 N/cm^2: Bates et al., 2010). Higher specific tensions are not exclusive to reptiles and increase with moderate pennation in mammals. For example, in vivo, isometric ST of human quadriceps ranges between 55 and 60 N/cm^2, consistently across age and sex (O'Brien et al., 2010).
No one ST value or derived force can be definitive. However, muscle force scales linearly with ST, and the effects of different ST estimates can be calculated with simple ratios. Sensitivity analyses tabulating (potentially infinite) variations are unproductive when parameter influences on each other are well-understood (Bates et al., 2010). As with specific tension, we did not run sensitivity analyses of the effects of muscle force on accelerations and velocities, because these quantities scale directly and predictably with forces and moments.
Application of Joints and Forces
We placed markers for joints and muscle attachments by translating, rotating, and scaling the model view to ensure that the markers were on the desired locations. Forces were input as line-of-sight vectors between markers, from origin (on the "reaction" body in Adams) to insertion (on the "action", primary moving body). Muscles were constrained to pass through via points when necessary, particularly for m. transversospinalis capitis, which runs along the dorsal curvature of the neck (Snively and Russell, 2007b). Force directions change during simulations, as markers for origins and insertions move relative to each other. Joints function smoothly when their markers on the articulating objects share the same global coordinate position and local coordinate axes. Appendix 3 details how to position coincident joint markers in Adams.
We applied two kinds of joints to the model, Hooke or universal joints which allow rotation about two orthogonal axes parallel to the joint surface, restricting four degrees of freedom (DOF), and revolute joints which allow rotation about a single axis, either horizontal or vertical for respective dorsoventral and lateral motions, restricting five DOF. For kinematic simulations, universal joints restricted translation while enabling other motions. For simulating accelerations of the head at the occipito-atlantal articulation, we applied revolute joints that would allow lateral and dorsoventral movements in respective analyses.
Simulations and Justification for Assessed Qualities of Motion
Simulating dynamics beyond anatomically feasible ranges of motion would be uninformative about Allosaurus biology.We therefore simulated kinematics (motion without forces), in lateroflexion, dorsal and ventral flexion, protraction, and retraction, to determine the ranges of motion for dynamic simulations. We specified angular velocities at each joint: 0.2 rad/s for joints between C9, C8, and C7; 0.25 rad/s for the remaining intervertebral joints, and 0.3 rad/s for movement of the skull at the occipito-atlantal joint. More rapid movements caused posterior vertebrae to overlap more quickly than anterior elements. We simulated each motion until bone geometry overlapped, and animated results for the longest realistic durations.
Dynamic simulations tested the hypothesis that contraction of m. longissimus capitis superficialis caused ventroflexion. Revolute joints at the C1-occipital condyle junction enabled motions, and fixed joints restricted motion elsewhere. We applied muscle forces that would drive the dynamics simulation, activating potentially ventroflexive muscles, and deactivating all others. We activated m. longissimus capitis superficialis alone to determine if it had a ventroflexive action. Gravity was active for all simulations.
RESULTS
External and Air-space Geometry
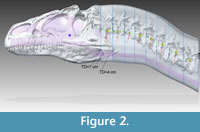
Figure 2 shows the Adams CT-based bone geometry registered to the Solid Edge lofted models, including external geometry and air spaces, and subsequent figures show geometry and centers of mass in more detail. Centers of mass and volume (colored spheres) are based on models without air spaces. Figure 3 depicts geometry of the anterior segment of the neck fitting between the paroccipital retroarticular processes of the skull. The elliptical cross section of the head excludes cranial ornamentation and includes the space between the ridges of the nasals.
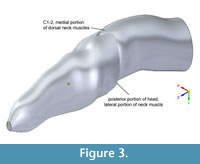Figure 4, Figure 5, and Figure 6 depict the head and air spaces in canonical views. Figure 4 shows how lofting in Solid Edge caused constriction of the trachea and posterior displacement of the choanae where the nasal airway meets the oral cavity (compare Figure 1 with Figure 2 and Figure 4). In life the olfactory region and suborbital sinus would be separate. The middle ear space (pharyngotympanic sinus) is far posterior to the olfactory region (Figure 4), and appears proportionally smaller than in other large theropods (Witmer and Ridgely, 2008; Dufeau, 2011); its 
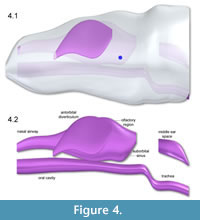small size relative to the airway is especially evident in dorsal or ventral view (Figure 5). The reconstructed antorbital diverticula (air sacs in front of the eyes) are perhaps angled inwards more than was probable in life (Figure 6), to fit within the contours of the head geometry consisting of lofted ellipses. A more rectangular cross section, such as with anatomically realistic super-ellipses, would better encompass the diverticula. Solid Edge cannot easily parameterize cross sections shaped like rounded rectangles.
Mass, Centers of Mass, and I of Allosaurus Head and Neck Segments
Table 1, Table 2, Table 3, Table 4, and Table 5 list centers of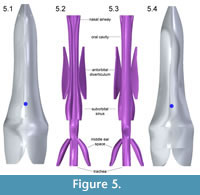 
mass, volumes, masses, and moments of inertia of Solid Edge models of Allosaurus. Table 1 lists centers of mass (COM) for the neck assuming a solid model and with tracheas at the two estimated diameters and for the head with uniform density and with air spaces. For the neck segments, COM shifts posteriorly and dorsally by 2–5 mm as tracheal size increases (Figure 7). The head COM moves 19 mm downwards for the head with air spaces versus a solid model (Table 1).
Table 2 lists volumes, masses, and I for neck segments and the head assuming no air spaces and a uniformassigned density, ρtissue, of skeletal muscle (1060 kg/m^3). Axes of rotation are oriented as in Figure 7, but (x,y,z) from Solid Edge in Table 2, Table 3, and Table 4 are equivalent to Adams axes (y,z,x) in the figure. Table 2, Table 3, and Table 4 explain all axes, and how I about these affect different types of rotation.
Head Inertial Properties with Varied Estimates of Tissue Density
Table 3 lists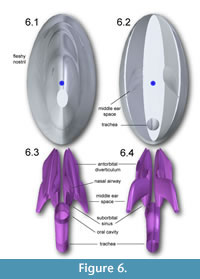
tissue volumes and inertial properties of the head of Allosaurus, calculated assuming soft-tissue density of 1050 kg/m^3 (Witmer and Ridgely 2008), air spaces present, and varying densities of bone (Witmer and Ridgely, 2008; Dumont, 2010). Mass varies between 25 and 30.6 kg; the higher masses assume compact bone with ρB in the avian range (Dumont, 2010). With ρB set to the average for large amniotes (Witmer and Ridgely, 2008), mass and I are lower than in a model with a uniform, average density of 1050 kg/m^3 (Table 2). With ρB set to a value common for mammalian compact bone (Cowin, 2001; Dumont, 2010), head mass of 27.46 kg is similar to that of the solid model (27.69 kg). However, Iyy is substantially greater in the realistic air space model (0.38 versus 0.35 kg m^2), because its COM shifts posteriorly relative to that of the solid model (Table 1).
Effects of Estimated Tracheal Size on Mass and I
Table 4 presents mass and I of neck segments, with respective tracheal diameters of 6.768 and 4 cm. Izz with the smaller trachea is approximately 6% greater than with the larger trachea, and Iyy is 2% greater. This result indicates that tracheal size has the greatest effect on mass moment of inertia about a mediolateral axis, which most strongly affects dorsoventral motion.
Fmax of Muscles
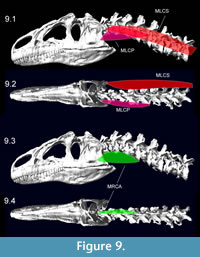
Figure 8 shows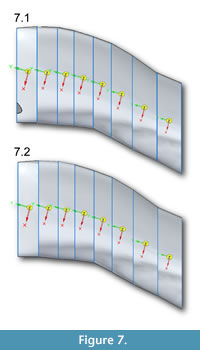
muscle attachments for ventroflexive muscles, and Figure 9 depicts the muscles reconstructed as slender. Table 5 lists muscle dimensions and forces from both slender and robust reconstructions; the latter have cross-sectional areas and Fmax 21% greater than in the slender, baseline reconstructions. The lateroflexor m. longissimus capitis superficialis and dorsiflexor m. transversospinalis capitis have the largest values of Fmax. 
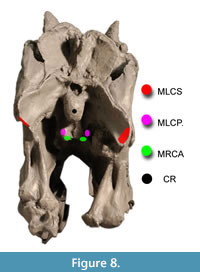As reconstructed, the ventroflexors also have high Fmax. Isometric force of m. longissimus capitis profundus, at 1777 N, is nearly as great as that of the large dorsiflexor m. transversospinalis capitis. Apparent cross-sectional areas of the ventroflexors would diminish as the head and neck are dorsiflexed, and their high Fmax values must be treated cautiously.
Kinematics: Apparent Ranges of Motion
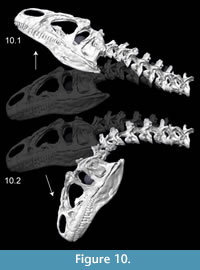
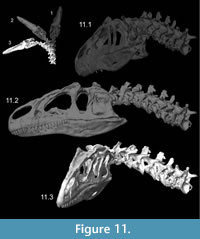
Kinematics figures depict endpoints of animations illustrating range of motion in Allosaurus, with the lateral articulations (zygapophyses) shifting by 40–50% overlap from a neutral posture. Dorsiflexion, especially at the head, was undoubtedly greater than seen here (Figure 10). The lateral range of motion evident in Figure 11 maintains smooth contact of the zygapophyses, without overlap of their modeled geometry, suggesting that greater lateral range of motion was possible. Range of motion for retraction appears to be substantial, by dorsiflexion of the postertior portion of the neck and ventroflexion of its anterior curvature (Figure 12).
Dynamics: Ventroflexive Accelerations
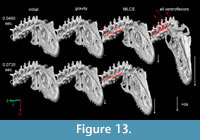
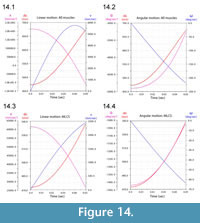
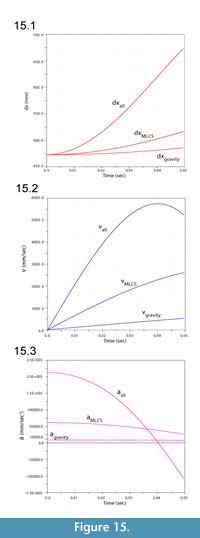
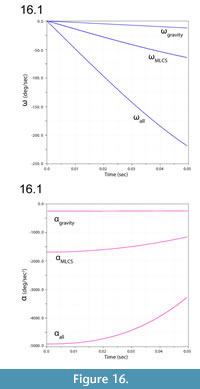
Figure 13 illustrates ventroflexion of the head of Allosaurus for two different durations, simulated under gravity alone, gravity plus m. longissimus capitis superficialis (MLCS), and with all muscles and gravity active for the shorter time (0.0495 sec) it took for the head to face downwards. Figure 14 graphs muscle-involved accelerations and velocities. Tangential acceleration behaves as expected under gravity alone (Figure 15). Muscle-driven simulations displace the tip of the premaxilla appreciably compared with gravity; this is especially evident for all muscles and for MLCS alone over the longer duration (0.0735 sec: Figure 13). For all of these simulations, Figure 14, Figure 15, and Figure 16 plot translational accelerations and velocities of the tip of the premaxilla (a, v) and rotational accelerations and velocities of the skull (α and ω; Figure 16). The muscle hypothesized as ventroflexing the head of Allosaurus, MLCS, contributed 26% of the total maximum muscle-driven ventroflexive acceleration. With this muscle activated alone, the anterior tip of the premaxilla reached 25% of the final angular and tangential velocities that this point attained with all muscles activated (Figure 14, Figure 15, and Figure 16).
The rate of ventral acceleration by all muscles starts to diminish after 0.04 sec (Figure 14.1, Figure 15.2, and Figure 15.3), as muscle lines of action become less favorable and the skull reaches its maximum ventroflexive position. MLCS still contributes to ventroflexion at and beyond this position, but other ventroflexors begin to exert a stronger retractive acceleration (in the +z direction: Figure 14).
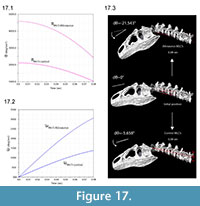
Figure 17 illustrates greater angular acceleration α with the inferred anatomical insertion of MLCS versus a control position resembling that in other theropods. The 2.5 times greater absolute value of α at the start of the simulation decreases to 2.2 times at 0.08 seconds. After this duration, the angular displacement dθ for the correct insertion is 3.8 times that of the control.
DISCUSSION
Head masses in our model of Allosaurus are 40–48% of best-estimate values calculated by Bates et al. (2009) for the same specimen. Bates et al. (2009) widened the head by 20% to correct for taphonomic crushing and we widened it by 5%. Because the length and height of the head are about the same in both studies, mass and mass moments of inertia are likely to vary directly with model width. Other probable reasons for the discrepancy include ellipses in our model compared with the straight-edged splines used by Bates et al. (2009), the dorsal concavity in our model between the parietals and lacrimal horns (Figure 2, Figure 3, and Figure 4), the cut-out of neck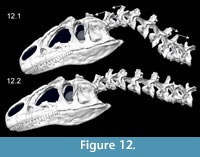 
muscles at the back of the head in our model, and our reconstruction of sinuses and airways (after Witmer, 1997 and Dufeau, 2011) resulting in a lower head density. Although our use of CT-based dimensions might appear to better approximate the original head shape, Bates et al. (2009) undoubtedly better corrected for crushing, and their octagonal splines better captured the squared-off cross-sectional shape of the head between the lower jaws. The head mass moments of inertia for Allosaurus in Bates et al.'s (2009) model were computed about the center of mass of the body, rather than the head as we have done, and it is inappropriate to compare these I values between the studies. By using the parallel axis theorem to compute I values for the head about estimated whole-body centers of mass (Bates et al., 2009), the results are driven by the mass of the head and are again 40–48% of Bates et al.'s values.
Our model's transverse cross sections were ellipses, and differing shapes (Appendix 1) have predictable effects on dynamics results. More squared-off superellipsoid cross sections (with exponents of 2.3–2.5 common in vertebrates: Motani, 2001) would increase mass by 5–7%, and I by 10–16% (Appendix 1, Table A1). These values would correspondingly reduce protraction and retraction performance (mass), and rotational acceleration and velocity (I).
Unusual Allosaurus Muscle Insertions Substantially Enhanced Ventroflexive Torque
Ventroflexion simulations support the hypothesis that m. longissimus capitis superficialis enhanced ventroflexive acceleration, to over twice the magnitudes of a control analysis with a "normal" theropod insertion. Under simulated conditions (and simplified assumptions), the muscle contributes a quarter of the total-muscle driven ventroflexive acceleration (excluding gravity) in this specimen of Allosaurus. This specimen was distorted slightly during fossilization, and its left paroccipital process runs more directly posterolaterally than in other specimens which have a more ventral course to the processes (Bakker, 1998[2000]); eight specimens examined by Snively and Russell, 2007a, 2007c). Because this latter anatomy indicates greater ventroflexive moment arms, our model is conservative, and we predict that dynamics simulations of other specimens will corroborate the hypothesis for Allosaurus.
Implications for Allosaurus Prey Capture and Feeding
These analyses indicate that ventroflexive angular acceleration in Allosaurus was greater than calculated for Tyrannosaurus (Snively and Russell, 2007c), as was predicted by some previous studies (Bakker, (1998[2000]); Rayfield et al., 2001; Snively and Russell, 2007c). Forceful ventroflexion supports the hypothesis that Allosaurus augmented its bite force by ventroflexing its upper jaws (Bakker, 1998[2000]; Rayfield et al., 2001), and suggests that it could strike downwards quickly.
Dorsoventral and protractive ranges of motion mirror those observed (Snively, 2006) and examined radiographically (Samman, 2006) in volant raptorial birds and inferred in the terrestrial phorusrhacid, Andagalornis (Tambussi et al., 2012). These ranges of head position suggest the efficacy of striking prey in the sagittal plane. In the posterior portion of the neck, lateral range of motion appears to be greater than observed in extant birds (Samman, 2006; Snively, 2006). Anteriorly, the lateral intervertebral range of motion is similar to that of the bald eagle Haliaeetus leucocephalus and snowy owl Bubo scandiacus (Samman, 2006), and greater than in Tyrannosaurus rex (figure 6.12 in Samman, 2006, Samman, in press; also examined preliminarily by Snively and Russell, 2007b). Neck and cervicocephalic range of motion in Allosaurus will be testable more thoroughly with methods that Stevens and Parrish applied to sauropods (Stevens and Parrish, 1998; Stevens and Parrish, 2005a, b), and Samman (2006; Samman, in press) used for tyrannosaurids.
Range of motion and accelerations may be informative about how Allosaurus defleshed its prey. Strong ventroflexive torque suggests a more birdlike posterior pull on a carcass than crocodilian-like shake-feeding. (The latter is more likely in tyrannosaurids [Snively and Russell, 2007a, c; Witmer and Ridgely, 2009], with their great moment-generating capacity to decelerate and reverse direction of the head [Snively and Russell, 2007a]). With posterior neck dorsiflexors and anterior head ventroflexors acting in concert for head retraction, Allosaurus may have fed more like a large predatory bird than like a crocodile (Snively, 2006; Snively and Russell, 2007a, c). However, Allosaurus was probably not limited to a single strategy for removing flesh. Its laterally compressed, ziphodont teeth suggest forceful alternating tugs to either side of the head, as seen in Komodo dragons (Auffenberg, 1981, D'Amore et al., 2011).
The greatest magnitudes of retractive (posteroventral) acceleration of the head in the Allosaurus simulations occur when the head is deeply flexed relative to the neck, suggesting parallels to how specific raptorial birds strip flesh. Merlins (Falco columbarius), with large ventroflexors, are adept at bracing prey with their feet, holding flesh with the head highly flexed, and pulling up and back with their legs (Snively, 2006) to tear muscle and other tissue from prey. Although Allosaurus has large bladelike teeth and lacks the hooked beak of raptorial birds, similarly energetic ventroflexion may have enabled analogous behavior. Assessing the likelihood of such action awaits full-body simulations that combine leg and neck function.
Refinement and Future Directions
The current dynamic simulations were restricted to head movement only and with constant force magnitude. Applying force-velocity and force-length relationships (Curtis et al., 2008, 2010a, b; Moazen, 2008a, b; Winters et al., 2011) will enable circumscribed ranges of Allosaurus musculoskeletal accelerations and tests of how muscle force parameters influence the results. Current advances with MSC Adams (Kumbhar and Cotton, unpublished data) incorporate complex spring-damper splines, that include high-force eccentric contraction (at negative velocity when a muscle produces force as it lengthens: Snively and Russell, 2007a; Miller et al., 2012). We predict diminished acceleration under two conditions: as muscles become much shorter or longer than estimated "optimal" lengths and at rapid contraction velocities (Domire and Challis, 2010; Miller et al., 2012). Conversely, we predict greater magnitudes of acceleration (actually deceleration) when muscles contract eccentrically to slow the head and neck as they approach their limits of excursion (Miller et al., 2012).
In addition to physiologically varying muscle force, refined articulations (including joint cartilages: Samman, 2006) will enhance confidence in our simulations. Spherical joints may simulate ball-and-socket articulations in Allosaurus more realistically than the revolute joints used here. Another potential advance will be to model articulations as contact surfaces, instead of revolute or spherical joints. This method has enabled accurate simulations of pig chewing (Kumbhar and Cotton, unpublished data) which track radiographically recorded kinematics (Brainerd et al., 2010).
The increased sophistication of these methods will narrow the probable range of feeding accelerations in Allosaurus, but will not necessarily increase our certainty about possible and habitual behaviors. Most physiological variables will remain unknown. Simpler models, with results falling within the range from complex analyses, may bring us close enough for informative comparisons between Allosaurus and other contemporary predators.
There are three independent ways to assess how informative our simulations might be. First, studies integrating physiology, morphology, and behavioral observation ("Extant Behavioural Interpolation": Snively, 2006; Snively and Russell, 2007c) enable systematic inference of behavior in fossil animals relative to their living relatives (Witmer, 1997). Second, correlating homologous muscle size with attachment morphology (Snively and Russell, 2007a) will become more quantitatively rigorous and specific with more studies of extant reptiles. Third, dynamic models of feeding in extant vertebrates (Moazen et al., 2008a, b; Curtis et al., 2009, 2010a, 2010b; Bates and Falkingham, 2012) enable validation of modeling methods against experimental results and measureable parameters.
Validation studies on modern animals, especially crocodilians and birds, are the next major step in modeling archosaur feeding dynamics. Starting with an extinct dinosaur, however, revealed hypotheses of neck retraction that will be applicable to birds. A crocodilian model would not have suggested similar kinematics, because their necks lack an anterior, dorsally convex curvature. Finally, manipulation of a virtual Allosaurus model may reveal restrictions on muscle paths that neither crocodilians nor birds possess. Multibody dynamics of large dinosaurs can help resolve and advance otherwise intractable hypotheses of functional morphology (Mallison, 2007, 2010; Sellers et al., 2009; Bates and Falkingham, 2012).
ACKNOWLEDGMENTS
Two anonymous reviewers fundamentally improved the manuscript. We thank M. Loewen for advice on specimens of Allosaurus, and N. Curtis and M. Moazen for discussions on using MSC Adams software. A.N. Vasavada gave us perspective on musculoskeletal dynamics software. P. May (Research Casting International) generously loaned us casts of the Allosaurus vertebrae. We thank students and associates of the Witmer, Cotton, Stevens-O'Connor, and Williams labs for discussions. This research was funded by the Russ College of Engineering and Technology, the Heritage College of Osteopathic Medicine, and a Research Challenge Grant (all Ohio University), as well as grants to LMW and RCR from the United States National Science Foundation (IBN-0343744, IOB-0517257, IOS-1050154). The Ohio Supercomputing Center also provided support. For assistance with CT scanning the Allosaurus skull and neck casts, we thank Heather Rockhold, RT, and O'Bleness Memorial Hospital, Athens, OH.
REFERENCES
Antón, M., Sánchez, I.M., Salesa, M.J., and Turner, A. 2003. The muscle-powered bite of Allosaurus: an interpretation of cranio-dental morphology. Estudios Geológicos, 59:313-323.
Auffenberg, W. 1981. The Behavioral Ecology of the Komodo Monitor. University of Florida Press, Gainesville.
Bakker, R.T. 1998(2000). Brontosaur killers: Late Jurassic allosaurids as sabre-tooth cat analogues. Gaia,15:145-158.
Bates, K.T. and Falkingham, P.L. 2012. Estimating maximum bite performance of Tyrannosaurus rex using multi-body dynamics. Biology Letters, doi:10.1098/rsbl.2012.0056.
Bates, K.T., Falkingham, P.L., Breithaupt, B.H., Hodgetts, D., Sellers, W.I., and Manning, P.L. 2009. How big was 'Big Al'? Quantifying the effect of soft tissue and osteological unknowns on mass predictions for Allosaurus (Dinosauria: Theropoda). Palaeontologia Electronica, 12(3):33 pp. http://palaeo-electronica.org/2009_3/186/index.html
Bates, K.T., Manning, P.L., Margetts, L. and Sellers, W.I. 2010. Sensitivity analysis in evolutionary robotics simulations of bipedal dinosaur running. Journal of Vertebrate Paleontology, 30:458-466.
Benson, R.B.J., Butler, R.J., Carrano, M.T., and O'Connor, M.P. 2012. Air-filled postcranial bones in theropod dinosaurs: physiological implications and the 'reptile'–bird transition. Biological Reviews, 87:168-193.
Brainerd, E.L., Baier, D.B., Gatesy, S.M., Hedrick, T.L., Metzger, K.A., Gilbert, S.L., and Crisco, J.J. 2010. X-ray Reconstruction of Moving Morphology (XROMM): precision, accuracy and applications in comparative biomechanics research. Journal of Experimental Zoology, 313A:262-279.
Britt, B.B. 1993. Pneumatic postcranial bones in dinosaurs and other archosaurs. PhD thesis. University of Calgary, Alberta.
Brochu, C.A. 2003. Osteology of Tyrannosaurus rex: insights from a nearly complete skeleton and high-resolution computed tomo- graphic analysis of the cranium. Journal of Vertebrate Paleontology,24(Supplement to 4):1-138.
Brusatte, S.L. and Sereno, P.C. 2007. Phylogeny of Allosauroidea (Dinosauria: Theropoda): comparative analysis and resolution. Journal of Systematic Palaeontology, 6:155-182.
Carrano, M.T., Benson, R.B.J., and Sampson, S.D. 2012. The phylogeny of Tetanurae (Dinosauria: Theropoda). Journal of Systematic Palaeontology, 10:211-300.
Chure, D.J. 2000. A new species of Allosaurus from the Morrison Formation of Dinosaur National Monument (UT-CO) and a revision of the theropod family Allosauridae. PhD thesis, Columbia University, New York City, New York, USA.
Cowin, S.C. 2001. Bone Mechanics Handbook, Second Edition. CRC Press, Boca Raton.
Curtis, N., Jones, M.E.H., Evans, S.E., O'Higgins, P., and Fagan, M.J. 2009. Visualising muscle anatomy using three-dimensional computer models - an example using the head and neck muscles of Sphenodon. Palaeontologica Electronica, 12,7T: 18p, http://palaeo-electronica.org/2009_3/194/index.html
Curtis, N., Jones, M.E.H., Evans, S.E., O'Higgins, P., and Fagan, M.J. 2010a. Predicting muscle activation patterns from motion and anatomy: modelling the skull of Sphenodon (Diapsida: Rhynchocephalia). Journal of the Royal Society Interface, 7:153-160.
Curtis, N., Jones, M.E.H., Lappin, A.K., Evans, S.E., O'Higgins, P., and Fagan, M.J. 2010b. Comparison between in vivo and theoretical bite performance: using multi-body modelling to predict muscle and bite forces in a reptile skull. Journal of Biomechanics, 43:2804-2809.
Curtis, N., Kupczik, K., O'Higgins, P., Moazen, M., and Fagan, M.J. 2008. Predicting skull loading: applying multibody dynamics analysis to a macaque skull. Anatomical Record, 291:491-501.
D'Amore, D.C., Moreno, K., McHenry, C.R., and Wroe, S. 2011. The effects of biting and pulling on the forces generated during feeding in the Komodo Dragon (Varanus komodoensis). PLoS ONE, 6(10):e26226.
Delp, S.L. and Loan, J.P. 1995. A graphics-based software system to develop and analyze models of musculoskeletal structures. Computers in Biology and Medicine, 25:21-34.
Domire, Z.J. and Challis, J.H. 2010. A critical examination of the maximum velocity of shortening used in simulation models of human movement. Computer Methods in Biomechanics and Biomedical Engineering, 13:693-699
Dufeau, D.L. 2011. The evolution of cranial pneumaticity in Archosauria: patterns of paratympanic sinus development. PhD Thesis. Ohio University.
Dumont, E.R. 2010. Bone density and the lightweight skeletons of birds. Proceedings of the Royal Society B: Biological Sciences, 277:2193-2198.
Foster, J. 2007. Jurassic West. Indiana University Press, Bloomington.
Fowler, M.E. 1991. Comparative clinical anatomy of ratites. Journal of Zoo and Wildlife Medicine, 22:204-227.
Gordon, A.M., Huxley, A.F., and Julian, F.J. 1966. The variation in isometric tension with sarcomere length in vertebrate muscle fibres.Journal of Physiology,184:170-192.
Henderson, D.M. 1999. Estimating the masses and centers of mass of extinct animals by 3-D mathematical slicing. Paleobiology, 25:88-106.
Hinds, D.S. and Calder, W.A. 1971. Dead air space in the respiration of birds. Evolution, 25:429-440.
Holtz, T.R., Jr., Molnar, R.E. and Currie, P.J. 2004. Basal Tetanurae, p. 71-110. In Weishampel, D.B., Dodson, P., and Osmolska H. (eds.), The Dinosauria, 2nd edition. Berkeley: University of California Press.
Loewen, M.A. 2009. Variation in the Late Jurassic theropod dinosaur Allosaurus: ontogenetic, functional, and taxonomic implicationsPhD thesis, University of Utah, Salt Lake City, Utah, USA.
Madsen, J.H., Jr. 1976. Allosaurus fragilis: a revised osteology. Bulletin 209, Utah Geological Survey.
Mallison, H. 2007. Virtual Dinosaurs - Developing Computer Aided Design and Computer Aided Engineering Modeling Methods for Vertebrate Paleontology. Ph.D. dissertation. Eberhard-Karls-Universität, Tübingen. http://tobias-lib.ub.uni-tuebin- gen.de/volltexte/2007/2868/
Mallison, H. 2010. The digital Plateosaurus I: body mass, mass distribution and posture assessed using CAD and CAE on a digitally mounted complete skeleton. Palaeontologica Electronica, 13(2) 8A:26p.
palaeo-electronica.org/2010_2/198/index.html
Marin, F., Hoang, N., Aufaure, P., and Ho Ba Tho, M.-C. 2010. In vivo intersegmental motion of the cervical spine using an inverse kinematics procedure. Clinical Biomechanics, 25:389-396.
Miller, R.H., Umberger, B.R., and Caldwell G.E. 2012. Sensitivity of maximum sprinting speed to characteristic parameters of the muscle force–velocity relationship. Journal of Biomechanics, 45:1406-1413.
Moazen, M., Curtis, N., Evans, S.E., O'Higgins, P., and Fagan, M.J. 2008a. Rigid-body analysis of a lizard skull: Modelling the skull of Uromastyx hardwickii. Journal of Biomechanics, 41: 1274-1280.
Moazen, M., Curtis, N., Evans, S.E., O'Higgins, P., and Fagan, M.J. 2008b. Combined finite element and multibody dynamics analysis of biting in a Uromastyx hardwickii lizard skull. Journal of Anatomy, 213:499-508.
Motani, R. 2001. Estimating body mass from silhouettes: testing the assumption of elliptical body cross sections. Paleobiology,27:735-750.
O'Brien, T.D., Reeves, N.D., Baltzopoulos, V., Jones, D.A., and Maganaris, C.N. 2010. In vivo measurements of muscle specific tension in adults and children. Experimental Physiology, 95: 202-210.
O'Connor, P.M. 2004. Pulmonary pneumaticity in the postcranial skeleton of extant Aves: a case study examining Anseriformes. Journal of Morphology, 261:141-161.
O'Connor, M. P. 2006. Postcranial pneumaticity: An evaluation of soft-tissue influences on the postcranial skeleton and the reconstruction of pulmonary anatomy in archosaurs. Journal of Morphology, 267:1199-1226.
Otten, E. 1987. A myocybernetic model of the jaw system of the rat. Journal of Neuroscience Methods, 21:287-302.
Rayfield, E.J., Norman, D.B., Horner, C.C., Horner, J.R., Smith, P.M., Thomason, J.J., and Upchurch, P. 2001. Cranial design and function in a large theropod dinosaur. Nature, 409:1033-1037.
Samman, T. 2006. Craniocervical functional morphology of several North American coelurosaurian dinosaurs. Unpublished PhD thesis, University of Calgary, Calgary, Alberta, Canada.
Samman, T. In press. Tyrannosaurid craniocervical mobility: a preliminary assessment. In Parrish, J.M., Molnar, R.E., Currie, P.J., and Koppelhus, E.B. (eds.), Tyrannosaurid Paleobiology. Indiana University Press, Bloomington.
Sellers, W.I., Manning, P.L., Lyson, T., Stevens, K., and Margetts, L., 2009. Virtual palaeontology: gait reconstruction of extinct vertebrates using high performance computing. Palaeontologia Electronica Vol. 12, Issue 3; 11A: 26p; http://palaeo-electronica.org/2009_3/180/index.html
Snively, E. 2006. Neck musculoskeletal function in the Tyrannosauridae (Theropoda, Coelurosauria): implications for feeding dynamics. Unpublished PhD thesis, University of Calgary, Calgary, Alberta, Canada.
Snively, E. 2012. Rigid body mechanics of prey capture in large carnivorous dinosaurs. Unpublished M.Sc. thesis, Ohio University, Athens, Ohio, USA.
Snively, E. and Russell A.P. 2007a. Functional variation of neck muscles and their relation to feeding style in Tyrannosauridae and other large theropods. Anatomical Record, 290:934-957.
Snively, E. and Russell, A.P. 2007b. Craniocervical feeding dynamics of Tyrannosaurus rex. Paleobiology, 33:610-638.
Snively, E. and Russell, A.P. 2007c. Functional morphology of neck musculature in the Tyrannosauridae (Dinosauria, Theropoda) as determined via a hierarchical inferential approach. Zoological Journal of the Linnean Society, 151:759-808.
Snively, E., Henderson, D.M., and Phillips, D.S. 2006. Fused and vaulted nasals of tyrannosaurid dinosaurs: Implications for cranial strength and feeding mechanics. Acta Palaeontologica Polonica, 51:435-454.
Stevens, K.A. and Parrish, J.M. 1998. Neck posture and feeding habits of two Jurassic sauropod dinosaurs. Science, 294:798-800.
Stevens, K.A. and Parrish, J.M. 2005a. Digital Reconstructions of Sauropod Dinosaurs and Implications for Feeding, p. 178-200. In Rogers, K.A.C. and Wilson, J.A. (eds.), Sauropods: Evolution and Paleobiology. University of California Press, Berkeley.
Stevens, K.A. and Parrish, J.M. 2005b. Neck posture, dentition, and feeding strategies in Jurassic sauropod dinosaurs, p. 212-232. In Tidwell, V. and Carpenter, K. (eds.), Thunder-Lizards: The Sauropodomorph Dinosaurs. Indiana University Press, Bloomington.
Tambussi, C.P., de Mendoza, R., Degrange, F.J., and Picasso, M.B. 2012. Flexibility along the neck of the Neogene terror bird Andalgalornis steulleti (Aves Phorusrhacidae). PLoS ONE, 7(5): e37701.
Tsuihiji, T. 2005. Homologies of the transversospinalis muscles in the anterior presacral region of Sauria (crown Diapsida). Journal of Morphology, 263:151-178.
Tsuihiji, T. 2007. Homologies of the longissimus, iliocostalis, and hypaxial muscles in the anterior presacral region of extant Diapsida.Journal of Morphology, 268:986-1020.
Tsuihiji, T. 2010. Reconstructions of the axial muscle insertions in the occipital region of dinosaurus: evaluations of past hypotheses on Marginocephalia and Tyrannosauridae using the Extant Phylogenetic Bracket approach. Anatomical Record, 293:1360-1386.
van Lopik, D.W. and Acar, M. 2007. Development of a multi-body computational model of human head and neck. Proceedings of the Institution of Mechanical Engineers Part K-Journal of Multi-Body Dynamics,221 Part K:175-197.
van Ruijven, L.J. and Weijs, W.A. 1990. A new model for calculating muscle forces from electromyograms. European Journal of Applied Physiology, 61:479-485.
Vasavada, A.N., Danaraj, J., and Siegmund, G.P. 2008a. Head and neck anthropometry, vertebral geometry and neck strength in height-matched men and women. Journal of Biomechanics, 41: 114-121.
Vasavada, A.N., Li, S., and Delp S.L. 1998. Influence of muscle morphometry and moment arms on the moment-generating capacity of human neck muscles. Spine, 23: 412-422.
Vasavada, A.N., Lasher, R.A., Meyer, T.E., and Lin, D.C. 2008b. Defining and evaluating wrapping surfaces for MRI-derived spinal muscle paths. Journal of Biomechanics, 41:1450-1457.
Wedel, M.J. 2005. Postcranial skeletal pneumaticity in sauropods and its implications for mass estimates. pp. 201-228. In Wilson, J.A. and Curry-Rogers, K. (eds.), The Sauropods: Evolution and Paleobiology. University of California Press, Berkeley.
Westneat, M.W. 2003. A biomechanical model for analysis of muscle force, power output and lower jaw motion in fishes. Journal of Theoretical Biology, 223:269-281.
Winters, T.M., Takahashi, M., Leiber, R.L., and Ward, S.R. 2011. Whole muscle length-tension relationships are accurately modeled as scaled sarcomeres in rabbit hindlimb muscles.Journal of Biomechanics, 44:109-115.
Witmer, L.M. 1997. The evolution of the antorbital cavity of archosaurs: a study in soft-tissue reconstruction in the fossil record with an analysis of the function of pneumaticity. Journal of Vertebrate Paleontology, 17(Supplement to 1): 1-73.
Witmer, L.M. and Ridgely, R.C. 2008. The paranasal air sinuses of predatory and armored dinosaurs (Archosauria: Theropoda and Ankylosauria) and their contribution to cephalic structure. Anatomical Record,291:1362-1388.
