Studying bipedal dinosaur trackways using geometric morphometrics
Article number: 22.3.pvc-3
https://doi.org/10.26879/980
Copyright Paleontological Society, September 2019
Author biographies
Plain-language and multi-lingual abstracts
PDF version
Submission: 7 March 2019. Acceptance: 8 August 2019.
{flike id=2708}
ABSTRACT
Traditionally, the study of dinosaur tracks and trackways has been helpful to learn about the anatomy of the trackmaker and its biodynamics. The implementation of digital techniques has further allowed delving into elusive evidence, such as the nature of autopod-substrate interaction and to build virtual collections. However, new methods that help to discriminate more objectively traits that lurk undetected within the tracks and the trackways are needed. Geometric Morphometrics (GM) is one of such advanced tools for shape analysis, but it has only been used for the comparison and ichnotaxonomic assessment of isolated footprints, and never for the study of dinosaur trackways. Using 2D GM, we analysed the differences between 75 randomly selected trackways of bipedal dinosaurs from literature, and tested if their variation was associated to the sizes of the trackways and to the estimated speeds at which the latter moved when leaving the trackways. Our results show that the method easily summarizes most of the trackway geometric differences, showing that such variation relates to footprint relative sizes, their orientation and their relative positions within the trackway. Importantly, the multivariate statistics indicated that none such differences could be attributed to ichnotaxa, while they clearly correlated with size, and in a much larger degree, to the estimated speeds at which the trackways were laid. Moreover, size and speed are unrelated, entailing that much of the trackway differences involve the biodynamics of bipedal dinosaurs, irrespective of their trackmaker assignment, plus substrate dynamics.
Mireia Costa-Pérez. Departamento de Botánica y Geología, Facultad de Ciencias Biológicas. Universidad de Valencia, Spain. mireiacostap@gmail.com
José Joaquín Moratalla. Instituto Geológico y Minero de España (IGME), Museo Geominero. Ríos Rosas, 23. 28003, Spain. j.moratalla@igme.es
Jesús Marugán-Lobón. Unidad de Paleontología, Dpto. Biología, Facultad de Ciencias. Universidad Autónoma de Madrid, Spain and Centre for the Integration in Paleobiology (CIPb), Universidad Autónoma de Madrid, Spain and Dinosaur Institute, Natural History Museum of Los Angeles County. Los Angeles, CA, USA. Corresponding author. jesus.marugan@uam.es
Keywords: bipedal dinosaurs; footprints; geometric morphometrics; paleoichnology; shape; trackways
Final citation: Costa-Pérez, Mireia, Moratalla, José Joaquín, and Marugán-Lobón, Jesús. 2019. Studying bipedal dinosaur trackways using geometric morphometrics. Palaeontologia Electronica 22.3.pvc_3, 1-13. https://doi.org/10.26879/980
palaeo-electronica.org/content/pvc-3
Copyright: September 2019 Paleontological Society.
This is an open access article distributed under the terms of Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0), which permits users to copy and redistribute the material in any medium or format, provided it is not used for commercial purposes and the original author and source are credited, with indications if any changes are made.
creativecommons.org/licenses/by-nc-sa/4.0/
INTRODUCTION
Dinosaurs have produced an exceptional record of ichnofossils, being probably the most complete and abundant of all vertebrates (Moratalla, 2008). Dinosaur trackways present quite a cosmopolitan distribution along the Mesozoic, making them a useful tool for biostratigraphy (Lockley et al., 1996) and for phylogenetic and taxonomic studies (Lockley et al., 2017). In addition, such a fossil record is useful to understand important aspects of the locomotion, behavior or ecology of terrestrial dinosaurs (Lockley, 1998), for establishing inferences about their behavior (Lockley, 1991), and, more generally, to extract information that complements that obtained from bones.
Because it is usually difficult to determine the authorship of the trackways, a typological classification is often used to associate general traits of the fossil footprints with the general anatomy of dinosaur ichnotaxa (Romilio and Salisbury, 2011). This lack of direct information has led paleoichology to rely heavily on morphometrics, as a way to minimize the ambiguity of purely qualitative descriptions (Moratalla et al., 1997, Xing et al., 2015). Thus, in dinosaur paleoichnology it is common to use measurements such as step and stride lengths and the relative orientation of the footprints, as descriptors of the trackways (Leonardi, 1987; Farlow et al., 1989). Moreover, such metrics can also be transferred to a biomechanical context (Alexander, 1976, 2006; Thulborn, 1990). By parameterizing the variables according to biophysical models of mass displacement, and putting them in association with knowledge of dinosaur anatomy, it is possible to model theoretical aspects of the biodynamics and the behavior of the dinosaurs. In fact, a common practice in dinosaur paleoichnology is to estimate the speed of displacement of the dinosaur at the moment of producing the trackway (if it was walking or running; Milan et al., 2006).
The morphological study of dinosaur tracks has traditionally been carried out on individual footprints (Lockley, 1991; Moratalla et al., 1997). The study of individual tracks has undergone a notable methodological evolution, especially in recent years, and from the traditional bivariate analysis of both variables and indexes (ratios) (Moratalla et al., 1988; Weems, 1992; Rasskin-Gutman et al., 1997), to the morphological analysis of strictly non-meristic characters. Notwithstanding this, several discussions have argued that is timely to start pushing new morphometric techniques further to and gain objectivity (Moratalla and Marugán-Lobón, 2009; Mathews et al., 2016; Falkingham, 2016).
On the other hand, the field of morphometrics has evolved drastically in the last two decades giving way to a new approach named Geometric Morphometrics (GM), a sophisticated tool that emerged as an alternative to overcome certain operational and visual limitations of traditional methodologies (Rohlf and Marcus, 1996, Adams et al., 2013). The operability of GM is based on the abstraction of form into a series of biologically homologous points called landmarks, whose Cartesian coordinates (2D or 3D), once transformed, forge the quantitative data which is thereafter submitted to multivariate statistical analysis (Bookstein, 1991). The comparisons are established by means of an algebraic process that superimposes the raw coordinates of the landmarks by translating, rotating and rescaling them, and is called the Procrustes superimposition. This procedure is based on the Least Squares criterion (Gower, 1975; Bookstein, 1991) and it has the important advantage of separating size from shape such that the former is conveyed as completely independent from the latter. At the same time, GM facilitates the visualization of the results through appealing graphics. These graphics have a reasonable similarity to the original forms and persuasively express the shape differences as landmark displacements or as smooth deformations of Cartesian grids. This, in turn, allows interpreting the results much more easily, avoiding the abstraction of biological change from complex algebraic relationships and raw numbers (Rohlf and Marcus, 1996). Although the algebraic and graphical advantages of GM are widely recognized in different fields of paleobiology, the fact is that the potential of the method in paleoichnology has been little explored.
Out of the few studies that have been carried out so far with GM, however, most have been performed for the comparison of isolated footprints (Rasskin-Gutman et al., 1997; Rodrigues and Santos, 2004; Moratalla and Marugán-Lobón, 2009), for ichnotaxonomic purposes (Shell and Boss, 2013), for comparing the variation of the shape of footprints within trackways (Lallensak et al., 2016) or the comparison of footprints between similar trackways (Castanera et al., 2015). The sources of variation between bipedal dinosaur trackways (their measurable geometric differences) might depend mainly on taxonomic (trackmaker identity) and preservational taphonomic factors, much as it does for isolated tracks (see Gatesy and Falkingham, 2017; Marchetti et al., 2019). The fact is that ichnotaxonomic allocation is not always exempt of certain ambiguity (Castanera et al., 2015) especially since a very large source of variation is due to substrate dynamics (Gatesy and Falkingham, 2017). On the other hand, it is not that clear how size might influence or determine trackway differences. On the other hand, the speed of the trackmaker can be determined from trackway parameters (e.g., stride length; Alexander, 1976), even if this approach is limited (Alexander, 2006). Arguably, then, the estimated speed for each trackway must be an element that accounts for part of the variability among the trackways. The question pending is what type of geometric difference it encompasses. Here, GM will be used to address the degree to which size, speed and taxonomy are contributing factors to the difference of bipedal dinosaur trackways in a randomly generated and reasonably large sample (N=75), and using custom multivariate toolkit of the method. The same will be applied to single tracks to further stress the important difference between comparing isolated tracks and trackways with GM.
MATERIALS AND METHODS
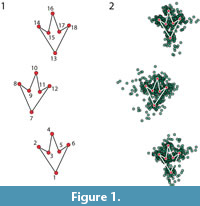The sample encompasses a total of 75 well-documented bipedal dinosaur trackways (51 theropods and 32 ornithopods), which were taken from literature (see Table 1). The original drawings of such trackways were digitized on a flatbed scanner and submitted to TPSdig2 (Rohlf, 2013) to obtain the landmarks. For simplicity, we chose to digitize only three tracks (footprints), as this number is the minimum required to describe a trackway (Thulborn, 1990). The number of tracks for the trackways can be as many as desired, yet all of them must have the same number of tracks that allow digitizing exactly the same landmarks. Notice as well that to be able to expand the sample as much as possible, it is possible to compare tracks that start with different feet (i.e., left or right), because it is easy to mirror the coordinates of the landmarks. Six landmarks were selected to capture the most salient features of a dinosaur tridactyl footprint (Figure 1, Table 2). Those six coordinates were repeated three times as a continuous series along the trackway, following a homology criterion for the correspondence of the landmarks in each track (i.e., left and right feet, respectively). Given that the choice is three tracks, the total number of landmarks in this study is 18.
The landmark coordinates were superimposed following a Generalized Procrustes superimposition criterion (Figure 1.2; Rohlf and Slice, 1990), which is the comparative procedure in Geometric Morphometrics and is applied to minimize the mismatch between landmark configurations using a Least Squares criterion (Gower, 1975). Such residual variation is usually referred as “shape”, it accounts for shape difference, and because it is multidimensional, it is best summarized using a Principal Components Analysis (PCA). The Procrustes superimposition performs a rigid superimposition (the configurations of landmarks are left intact after translation, rotation and scaling) and is therefore sensible to left and right symmetry. However, it is possible (and easy) to invert the coordinates to their mirror ones (Savriama and Klingenberg, 2012), and therefore, this is why it is possible to compare the tracks indistinctively of whether they start from one foot or another.
In principle, the main differences between trackways should partly be determined by the anatomy of the dinosaur, meaning that a certain amount of the differences between trackways should be taxonomical. To test this supposition, each of the trackways was assigned to a dinosaurian ichnotaxon, labeled as Ornithopod or Theropod, according to the criterion expressed in the original publication of the trackway. However, to verify statistically if there are any differences between the trackways and their alleged trackmaker, we performed a Discriminant Function Analysis (Klingenberg and Monteiro, 2005), because PCA does not consider group differences.
We also tested if the trackway shape differences and the estimated speed differences are statistically associated with size (i.e., size is the real scale of the trackway) using multivariate and bivariate linear regressions (Monteiro, 1999; Marugán-Lobón et al., 2013), respectively. These tests are a rough proxy to asking if trackway geometry and movement speed are related to the size of the producing dinosaur. Anatomy, size and biomechanics are biological inseparable, and therefore, we assume that a correlation must exist; the question is to what magnitude and in what sense. Size in GM is calculated as a scalar known as Centroid Size, which is extracted directly from the real distances between the landmarks within their configurations (the images were calibrated to real scale), and corresponds to the square root of the sum of the squared distances between the landmarks (Bookstein, 1991).
Finally, another multivariate regression was performed to test if there is any statistical correlation between the shape differences across the studied trackways (Figure 1) and the estimated speeds at which each of the dinosaurs allegedly walked or ran (Table 1). Namely, given that speeds can be calculated out of the geometry and size of the trackways, we hypothesize that there must be a correlation between the differences in Procrustes shape data of the trackways and the estimated speeds out of them. Thus, the null hypothesis is that different speeds should account for an unknown portion of the shape variance across trackways. The speed of each trackway was calculated following the formula by Alexander (1976) out of the scaled landmark configurations (extracted from the calibrated images) using Past (Hammer, 2011), and was used as an independent variable (x) in a multivariate regression model against the Procrustes shape residuals, with statistical significance evaluated by 10000 random iterations.
All the analyses were performed with MorphoJ (v. 106d; Klingenberg, 2010). GM is eminently a visual tool, and we have used part of the repertoire of methods to visualize the results (Klingenberg, 2014), including the deformation grids (Thin Plate Splines; Bookstein, 1991). In GM, the visualization logic is always to compare pairwise a reference configuration to a target one. This can be performed directly by showing both configurations superimposed, or with deformation grid depiction, inspired in D’Arcy Thompson’s deformation grids. The latter is based on the deformation of a Cartesian coordinate grid that is fit to the reference landmark configuration, and deformed to the target configuration of landmarks. Here, we used this to express the results of the PCA and the regressions, whereby the reference is the average configuration (Grand Mean or consensus) configuration, and the target is the score corresponding to each PC axis (the PCA) or the estimated shape scores (regression).
RESULTS
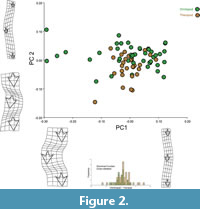The Procrustes shape residuals (Figure 1.2) show that the geometric (shape) differences between the trackways are quite large, which is observable from the large mismatch between configurations, shown as large departures of the residuals from the mean configuration. In fact, most of these differences involve not only the relative sizes of the tracks, but also their position along the trackway, of the second footprint relative to the first and the third. This coarse observation is resolutely verified by the PCA (Figure 2), where the largest difference between tracks, as accounted by PC1 (62% of explained variance), involves differences both in the relative sizes of the tracks and in the gauge of the trackway. PC2 (16%) accounts for the relative sizes of the tracks as well, yet along with more marked differences in the relative lengths of the steps, and the different footprint rotation relative to the midline axis of the trackway. The overlapping between alleged taxa in the PCA ordination is very large, implying that there is no taxonomic distinction between the shapes of the trackways. In fact, the discriminant function (shown below PC 1 axis in Figure 2) shows an almost complete overlapping between randomly iterated substitutions between groups (P=0.048, to a 1000 permutations test), implying that it completely fails to statistically assign taxa to trackway differences.
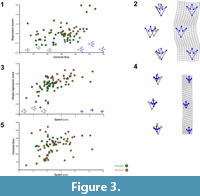Not surprisingly, there is a strong correlation between track shape variation with Centroid Size (11.3% explained variance; P<0.001; Figure 3.1), such that larger trackways have larger footprints (i.e., larger trackways were made by larger animals with larger feet and vice versa for the smaller ones) (Figure 3.2). More interesting is the statistically significant correlation between trackway shape data and speeds (15%; P<0.0001; Figure 3.3), indicating that at faster speeds there is a tendency to increase step length and reduce feet size, while also reducing the gauge (Figure 3.4). In fact, Centroid Size and Speed are not correlated (Figure 3.5), and the residuals from the regression to centroid size (i.e., the shape variation that is uncorrelated to size variation) is even better correlated with speed variation, associating exactly the same shape differences yet explaining up to 25% of the variance (P<0.0001). In sum, size and speed allow partitioning shape variance and amount for nearly 35% of the total differences across the studied trackways of bipedal dinosaurs.
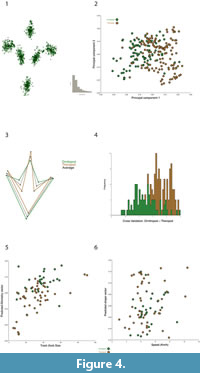For comparison, and to demonstrate the difference of studying tracks and trackways, we have performed exactly the same set of analyses on all the isolated tracks pertaining to the studied trackways. The main differences between the isolated tracks are their relative slenderness, the relative lengths of the digits and their gauges. Interestingly, although theropod footprints seem more slender and narrower (Figure 4.1-3), the cross validation (p<0.001) of a Discriminant function falsifies that this difference is statistically significant (Figure 4.4). Thus, it is also impossible to assign ichnotaxa to the tracks with geometric morphometrics and the landmarks that we used. Interestingly, however, the latter discriminant function suggests that footprint morphologies that fall at the left tail of the distribution can be assigned to ornithopods (i.e., those with relatively short and thicker digits with wider gauges), but this is only because they are extreme cases. Importantly, regressions show that there is no correlation between track shape variation and estimated speeds (%explained variance<0.6, P=0.7709; Figure 4.5), but there is a statistically significant allometric tendency in the sample (%explained variance=8.7, P=0.0001; Figure 4.6). The latter analysis predicts that smaller track sizes match the shape of theropod-like ichnotaxa (i.e., smaller tracks with more slender digits and smaller gauges), but this result is again clearly biased by outliers, namely, by a small pool of three theropod trackways that have the smallest tracks in the studied sample (i.e., they are feet size outliers).
DISCUSSION
Geometric morphometrics (GM) is a powerful tool for shape analysis increasingly used in multiple fields of paleontology. In paleoichnology the method has only been used to compare isolated tracks, mainly with the objective of obtaining fined-tuned assessments of track identity that help to discriminate between ichnotaxa (e.g., Castanera et al., 2015). However, GM has never been used to study trackway variation. The comparison of trackways encompasses information about the shape of the tracks (the footprints) but also the spatial differences between their orientations and position along the trail. Thus, it is not surprising that the analyses of isolated tracks yield different results from those of the trackways. This is self-evident when comparing the result of the Procrustes superimposition of Figure 1.2 and of Figure 4.1. In fact, the similarity of the results between analyses of the tracks and of the trackways is only because the shape differences between tracks are an important part of the variation contained within the differences between trackways. Thus, the advantage is that studying the trackways with GM entails assessing concomitantly footprint differences and if such differences are correlated with relative steps length, relative orientation and feet gauge.
Importantly, the power of GM increases when aiming to test the statistical covariation of shape with possibly related factors (Bookstein, 1991), yet this has seldom been exploited by any biological or paleontological discipline, in spite of its immense potential to aid discovery (Monteiro, 1999; Marugán-Lobón et al., 2013). Here we have shown that bipedal dinosaur trackways not only can be easily compared statistically and graphically using 2D GM, but also that the observed variation across trackways can be factored out to gain further insight. We have utilized variables that approximate the size of the trackmaker and the estimated speed at which the latter was moving at the moment of the production of the trackway to such end. The obtained results unambiguously showed that important differences between trackways are related to the size of the producer and, in a larger magnitude, to the pace at which it is estimated that the dinosaur was moving when imprinting the trackway. The differences between trackways, which are not associated to such factors (i.e., the remaining variance), is probably due to latent substrate dynamics and diagenetic factors.
The geometry of the tracks and the trackway bear indirect evidence of the anatomy of the trackmaker, which is why it can be a reliable proxy to interpret, or to infer, important aspects of the anatomy of the animal that produced it. However, the assignment of particular taxa to the trackways is often difficult, sometimes even impossible (Marchetti et al., 2019), because multiple factors influence the final shape of the tracks, including sediment structure and taphonomy, all of which can obscure ichnotaxonomic assignments. In fact, this is the reason why researchers have aimed at parsing subtle features of the footprints with fined-tuned proxies such as geometric morphometrics (Moratalla and Marugán-Lobón, 2009; Castanera et al., 2015). However, it has been impossible to discern any taxonomic characteristic out of the trackways, entailing that geometric differences assignable to the trackmaker’s identity are elusive to our landmark configurations. Furthermore, not only track shape, but none of the rest of the features that account for the shape differences across the studied trackways is attributable to taxonomic identity. Thus, any signal attributable to the trackmaker in the tracks and the trackways is definitely subtle, may be qualitative, may be fainted by preservation or may be related to features such as outlines, all of which are concealed to landmark data.
The use of PCA is very practical because the variance is summarized within a few explanatory dimensions of shape variance, enabling to easily see the differences between trackways (and tracks, when studied isolated). However, this analysis does not reveal any insight about the factors involved in such distribution. Here we hypothesized that size and speed probably underscored such patterns, but it is only via statistical inference (regression) that this can be tested. Namely, regressions showed that size (computed as Centroid Size) underscores part of the variability (i.e., the larger the trackways the larger the tracks, entailing that the larger the dinosaur, the larger the feet). This is an obvious finding, of course, because larger animals will produce larger trackways with larger footprints, and this is exactly what we found. The fact that we found this, in effect, would be the simplest proof that the method works, if it weren’t because we also found that size actually blurs the important association between the estimated speeds and the shape differences between tracks.
We had hypothesized that speed should be a biodynamic factor associated to the differences between trackways, because according to the geometry of the trackways, it is possible to estimate the speeds at which the dinosaurs were displacing at the moment of the production of the trackway (Alexander, 1976). We found that speed variation is highly correlated with trackway shape variance, entailing that speed is latently underlying a large portion of the observed pattern captured by the PCA. In spite of the limitations of estimating the speeds of the trackmakers from the trackways (Alexander, 2006; Moratalla et al., 2018), several things are noticeably important. First, according to the results, speed differences are associated to anatomical differences, such that dinosaurs that tended to move faster predictably had relatively smaller feet at lesser gauges, while performing relatively longer strides. Obviously, these parameters are intrinsically correlated because they are part of the speed formula, but the resulting variable has helped to factor out its sense out of the whole variation of the studied sample. Importantly, such pattern of speed and trackway variation is not correlated with size (size and speed are uncorrelated; Figure 3). Furthermore, the shape differences, which are devoid of the effect of size (i.e., the residuals that remain after regressing size to shape), are even better adjusted to speed differences. This finding further indicates that the variable speeds at which the trackway were made is a very important factor influencing the variability of the tracks. It is worth noting that much of the remaining variation is probably associated to substrate dynamics.
CONCLUSIONS
All the biodynamic information coming from trackways has derived from the application of traditional tools based on relatively elementary variables: stride length, step length, step angle, relative trackway width, rotation of the footprints in relation to the trackway midline, etc. (Alexander, 1976; Demathieu, 1984; Thulborn, 1990). These proxies have provided important conclusions about functional biodynamics in the locomotion of different groups of dinosaurs: progression speed, locomotion pattern, etc. In this study, we have devised a very simple GM protocol to study dinosaur trackways, not as a surrogate of traditional proxies, but as a complementary tool that will be helpful in paleoichnology. The GM approach is straightforward, and it can be extended to the analysis of other tetrapod trackways, of many more and much larger trackways (i.e., including many more trackways with many more tracks), both in 2D and in 3D. Of course, we have not put much attention to the preservation process (taphonomy), which is known to be an important distorting element of fossils (Gatesy and Falkiham, 2017). In fact, the loss of definition of the contour of the footprints that is generated in the different layers that underlie the footprint (known as undertracks), is a known difficulty that comes when differentiating these from the original traces (Lockley, 1991; Moratalla et al., 1997; Lockley, 1998). We have also discussed that taxonomic assignation is difficult probably because subtle features within the tracks may be qualitative, or they may reside in the tracks’ outlines. The GM protocol that we presented can further incorporate semilandmarks for capturing the outline variation among the tracks. However, semilandmarks can be problematic (Pérez et al. 2006), and the procedure would be more time consuming. Just as the size of the trackmaker and speed at which it was moving when producing the footprints, several other independent variables can be proposed as independent factors to factoring out shape variance. These include, for instance, age, geographic distribution and sedimentological composition, but there are infinite alternatives.
ACKNOWLEDGEMENTS
The authors are grateful to the organizers of the 1st Virtual Congress in Paleontology, for their initiative, hard work, and the invitation to participate in this volume. JML and JJM are endorsed by Project CGL2013-42643-P for the study of the Las Hoyas fossil site (Spain) funded by the Spanish Ministerio of Economía and Competitividad (MINECO).
REFERENCES
Adams, D.C., Rohlf, F.J., and Slice, D.E. 2013. A field comes of age: Geometric morphometrics in the 21st century. Hystrix, 24:7-14.
Alexander, R.M. 1976. Estimates of speeds of dinosaurs. Nature, 261:129-130. https://doi.org/10.1038/261129a0
Alexander, R.M. 2006. Dinosaur biomechanics. Proceedings of the Royal Society B, 273:1849-1855. https://doi.org/10.1098/rspb.2006.3532
Bookstein, F.L. 1991. Morphometric Tools for Landmark Data: Geometry and Biology. Cambridge University Press, Cambridge. https://doi.org/10.1017/cbo9780511573064
Castanera, D., Colmenar, J., Sauvé, V., and Canudo, J.I. 2015. Geometric morphometric analysis applied to theropod tracks from the Lower Cretaceous (Berriasian) of Spain. Palaeontology, 58:183-200. https://doi.org/10.1111/pala.12132
Casanovas, M.L., Ezquerra, R., Fernández Ortega, A., Pérez-Lorente, F., Santafé, J.V., and Torcida, F. 1993. Icnitas de dinosaurios. Yacimientos de Navalsaz, Las Mortajeras, Peñaportillo, Malvaciervo y La Era del Peladillo 2 (La Rioja, España). Zubía, 5:9-133.
Dalla Vecchia, F.M., Tunis, G., Venturini, S., and Tarlao, A. 2001. Dinosaur track sites in the upper Cenomanian (Late Cretaceous) of Istrian Peninsula (Croatia). Bolletino Della Società Paleontologica Italiana, 40:25-53.
Demathieu, G.R. 1984. Utilisation de lois de la mécanique pour l’estimation de la vitesse de locomotion des Vertebrés tétrapodes du passé. Geobios, 17:439-446. https://doi.org/10.1016/s0016-6995(84)80018-2
Falkingham, P.L. 2016. Applying objective methods to subjective track outlines, p. 296-333. In Falkingham, P.L., Marty, D., and Richter, A. (eds.), Dinosaur Tracks: The Next Steps. Indiana University Press, Bloomington.
Falkingham, P.L., Bates, K.T., Avanzini, M., Bennett, M., Bordy, E.M., Breithaupt, B.H., Castanera, D., Citton, P., Díaz-Martínez, I., Farlow, J.O., Fiorillo, A.R., Gatesy, S.M., Getty, P., Hatala, K.G., Hornung, J.J., Hyatt, J.A., Klein, H., Lallensack, J.N., Martin, A.J., Marty, D., Matthews, N.A., Meyer, C.A., Milan, J., Minter, N.J., Razzolini, N.L., Romilio, A., Salisbury, S.W., Sciscio, L., Tanaka, I., Wiseman, A.L.A., Xing, L.D., and Belvedere, M. 2018. A standard protocol for documenting modern and fossil ichnological data. Palaeontology, 61:469-480. https://doi.org/10.1111/pala.12373
Farlow, J.O., Pittman, J.G. and Hawthorne, J.M. 1989. Brontopodus birdi, Lower Cretaceous sauropod footprints from the U. S. Gulf Coastal Plain, p. 371-394. In Gillette, D.D. and Lockley, M.G. (eds.), Dinosaur Tracks and Traces. Cambridge University Press, Cambridge.
Gatesy, S.M. and Ellis, R.G. 2016. Beyond surfaces: A particle-based perspective on track formation, p. 335-380. In Falkingham, P.L., Marty, D., and Richter, A. (eds.), Dinosaur Tracks: The Next Steps. Indiana University Press, Bloomington.
Gatesy S.M. and Falkinham, P.L. 2017. Neither bones nor beet: Track morphological variation and ‘preservation quality’. Journal of Vertebrate Paleontology 37(3):e1314298.
Gatesy, S.M., Baier, D.B., Jenkins Jr, F.A., and Dial, K.P. 2010. Scientific rotoscoping: A morphology-based method of 3-D motion analysis and visualization. Journal of Experimental Zoology, 313A:244-261. https://doi.org/10.1002/jez.588
Gillette, D.D. and Lockley, M.G. (eds.). Dinosaur Tracks and Traces. Cambridge University Press, Cambridge.
Gower, J.C. 1975. Generalized procrustes analysis. Psychometrika, 40:33-51. https://doi.org/10.1007/bf02291478
Hammer, Ø., Harper, D.A.T., and Ryan, P.D. 2001. PAST: Paleontological statistics software package for education and data analysis. Palaeontologia Electronica, 4.1.4:1-9.
https://palaeo-electronica.org/2001_1/past/issue1_01.htm
Huh, M., Hwang, K.G., Paik, I.S., Chung, C.H. and Kim, B.S. 2003. Dinosaur tracks from the Cretaceous of South Korea: Distribution, occurrences and paleobiological significance. Island Arc, 12:132-144. https://doi.org/10.1046/j.1440-1738.2003.00386.x
Klingenberg, C.P. 2011. MorphoJ: An integrated software package for geometric morphometrics. Molecular Ecology Resources, 11:353-357. https://doi.org/10.1111/j.1755-0998.2010.02924.x
Klingenberg, C. P., and L.R. Monteiro. 2005. Distances and directions in multidimensional shape spaces: Implications for morphometric applications. Systematic Biology, 54:678-688. https://doi.org/10.1080/10635150590947258
Lallensack, J.N., van Heteren, A., and Wings, O. 2016. Geometric morphometric analysis of intratrackway variability: A case study on theropod and ornithopod dinosaur trackways from Münchehagen (Lower Cretaceous, Germany). PeerJ, 4:1-52. https://doi.org/10.7717/peerj.2059
Leonardi, G. 1987. Glossary and Manual of Tetrapod Footprint Palaeoichnology. Departamento Nacional da Produção Mineral, Ministério das Minas e Energia, Brasilia.
Lockley, M. 1991. Tracking Dinosaurs. A New Look at an Ancient World. Cambridge University Press, Cambridge.
Lockley, M., Gierlinski, G., Matthews, N., Xing, L., Foster, J., and Cart, K. 2017. New dinosaur track occurrences from the Upper Jurassic Salt Wash Member (Morrison Formation) of southeastern Utah: Implications for thyreophoran trackmaker distribution and diversity. Palaeogeography, Palaeoclimatology, Palaeoecology, 470:116-121. https://doi.org/10.1016/j.palaeo.2016.12.047
Lockley, M.G. 1998. Philosophical perspectives on theropod track morphology: Blending qualities and quantities in the science of ichnology. Gaia 15:279-300.
Lockley, M.G., Dos Santos, V.F., Meyer, C.A., and Hunt, A.P. 1998. A new dinosaur tracksite in the Morrison Formation Boundary Butte, southeastern Utah. Modern Geology, 23:317-330.
Lockley, M.G. and Hunt, A.P. 1999. Dinosaur Tracks and Other Fossil Footprints of the Western United States. Columbia University Press, New York.
Lockley, M.G. and Meyer, C.A. 2000. Dinosaur Tracks and Other Fossil Footprints of Europe. Columbia University Press, New York.
Lockley, M.G., Meyer, C.A., Schultz-Pittman R., and Forney, G. 1996. Late Jurassic dinosaur tracksites from central Asia: A preliminary report on the world’s longest trackways, p. 137-140. In M. Morales. (ed.), The Continental Jurassic. Museum of Northern Arizona Bulletin, Flagstaff.
Marchetti, L., Belvedere, M., Voigt, S., Klein, K., Castanera, D. Díaz-Martínez, I., Marty, D., Xing, L., Feola S., Melchor, R.N., and Farlow, J.O. 2019. Defining the morphological quality of fossil footprints. Problems and principles of preservation in tetrapod ichnology with examples from the Palaeozoic to the present. Earth-Science Reviews 193:109-145.
Marugán-Lobón, J., Buscalioni, A. D. 2006. Avian skull morphological evolution: Exploring exo- and endocranial covariation with Two-block Partial Least Squares. Zoology, 109:217-230. https://doi.org/10.1016/j.zool.2006.03.005
Marugán-Lobón, J., Blanco Miranda, D., Chamero, B., and Martín Abad, H. 2013. On the importance of examining the relationship between shape data and biologically meaningful variables. An example studying allometry with geometric morphometrics. Spanish Journal of Paleontology, 28(2):139-148.
Mathews, N., Noble, T., and Breithaupt, B. 2016. Close-range photogrametric for 3-D ichnology: The basics of photogrammetric ichnology, p. 127-240. In Falkingham, P.L., Marty, D., and Richter, A. (eds.), Dinosaur Tracks: The Next Steps. Indiana University Press, Bloomington.
Milan, J., Avanzini, M., Clemmensen, L.B, García-Ramos, J.C, and Piñuela, L. 2006. Theropod foot movement recorded by Late Triassic, Early Jurassic and Late Jurassic fossil footprints. New Mexico Museum of Natural History and Science Bulletin, 37:352-364.
Monteiro, L.R. 1999. Multivariate regression models and geometric morphometrics: The search for causal factors in the analysis of shape. Systematic Biology, 48(1):192- 199. https://doi.org/10.1080/106351599260526
Moratalla, J.J. 1993. Restos Indirectos de Dinosaurios del Registro Español: Paleoicnología de la Cuenca de Cameros (Jurásico superior-Cretácico inferior) y Paleoología del Cretácico Superior. Unpublished PhD Thesis, Universidad Autónoma de Madrid, Madrid, Spain.
Moratalla, J. 2008. Dinosaurios. Un Paseo entre Gigantes. Editorial EDAF, Madrid.
Moratalla, J.J. and Marugán-Lobón, J. 2009. Assessing dinosaur ichno-variability with geometric morphometrics. The ornithopod tracks from the Cameros Basin (Lower Cretaceous, Spain) as a case study. Journal of Vertebrate Paleontology, 29(3):151A.
Moratalla, J.J., Marugán-Lobón, J., Martín-Abad, H., Cuesta, E., and Buscalioni, A.D. 2017. A new trackway possibly made by a trotting theropod at Las Hoyas fossil site (Early Cretaceous, Cuenca Province, Spain): Identification, bio-dynamics, and palaeoenvironmental implications. Paleontologia Electronica, 20.3.59A:1-14. https://doi.org/10.26879/770
https://palaeo-electronica.org/content/2017/2073-theropod-trackway-at-las-hoyas
Moratalla, J.J., Sanz, J.L., and Jiménez, S. 1988. Multivariate analysis on Lower Cretaceous dinosaur footprints: Discrimination between ornithopods and theropods. Geobios, 21:395-408. https://doi.org/10.1016/s0016-6995(88)80042-1
Moratalla, J.J., Sanz, J.L., and Jiménez, S. 1997. Información paleobiológica y paleoambiental inferida a partir de las icnitas de dinosaurios: Problemas, límites y perspectivas. Revista Española de Paleontología, 12:185-196.
Moratalla, J.J., Sanz, J.L., and Jiménez, S. 1988. Multivariate analysis on Lower Cretaceous Dinosaur footprints: Discrimination between ornithopods and theropods. Geobios, 21(4):395-408. https://doi.org/10.1016/s0016-6995(88)80042-1
Pérez, S.I., Bernal, V., and González, P.N. 2006. Differences between sliding semi-landmark methods in geometric morphometrics, with an application to human craniofacial and dental variation. Journal of Anatomy, 208(6):769-784. https://doi.org/10.1111/j.1469-7580.2006.00576.x
Pérez-Lorente, F. 2015. Dinosaur Footprints and Trackways of La Rioja. Indiana University Press, Bloomington.
Rasskin-Gutman, D., Hunt, G., Chapman, R.E., Sanz, J. L., and Moratalla, J.J. 1997. The shapes of tridactyl dinosaur footprints: Procedures, problems and potentials. In D. L. Wolberg, E. Stump and G. D. Rosenberg (eds.), Dinofest International. Academy of Natural Sciences, Philadelphia.
Rodrigues, L.A. and Santos, V.F. 2004. Sauropod tracks: A geometric morphometric study, p. 129-142. In Elewa, A.M.T. (ed.), Morphometrics. Applications in Biology and Palaeontology. Springer, New York.
Rohlf, F. J. 2013. tpsDig, digitize landmarks and outlines, version 2.17. Department of Ecology and Evolution, State University of New York at Stony Brook.
Rohlf, F. J. and Corti, M. 2000. The use of two-block partial least-squares to study covariation in shape. Systematic Biology, 49:740-753. https://doi.org/10.1080/106351500750049806
Rohlf, F.J. and Marcus, L.F. 1993. A revolution in morphometrics. Trends in Ecology and Evolution, 8:129-132. https://doi.org/10.1016/0169-5347(93)90024-j
Rohlf, F. J. and Slice, D. E. 1990. Extensions of the Procrustes method for the optimal superimposition of landmarks. Systematic Zoology, 39:40-59. https://doi.org/10.2307/2992207
Romilio, A. and Salisbury, S.W. 2011. A reassessment of large theropod dinosaur tracks from the mid-Cretaceous (late Albian-Cenomanian) Winton Formation of Lark Quarry, central-western Queensland, Australia: A case for mistaken identity. Cretaceous Research, 32:135-142. https://doi.org/10.1016/j.cretres.2010.11.003
Savriama, Y. and Klingenberg, C.P. 2011. Beyond bilateral symmetry: Geometric morphometric methods for any type of symmetry. BMC Evolutionary Biology, 11:280. https://doi.org/10.1186/1471-2148-11-280
Shell, R. and Boss, S.K. 2013. Morphometric analysis of dinosaur tracks from Southwest Arkansas. Journal of the Arkansas Academy of Science, 67:121-130.
Thulborn, R.A. 1990. Dinosaur Tracks. Chapman and Hall, London.
Weems, R.E. 1992. A re-evaluation of the taxonomy of Newark Supergroup saurischian dinosaur tracks, using extensive statistical data from a recently exposed tracksite near Culpeper, Virginia. Proceedings 26th Forum on the Geology of Industrial Minerals, 119:113-127.
Xing, L., Lockley, M.G, Marty, D., Zhang, J., Wang, Y., Klein, H., McCrea, R.T., Buckley, L.G., Belvedere, M., Mateus, O., Gierliński, G.D., Piñuela, L., Scott Peterson, W., Wang, F., Ran, H., Dai, H., and Xie, X.. 2015. An ornithopod-dominated tracksite from the Lower Cretaceous Jiaguan Formation (Barremian-Albian) of Qijiang, South-Central China: New discoveries, ichnotaxonomy, preservation and palaeoecology. PLoS One, 10:1-44. https://doi.org/10.1371/journal.pone.0141059
Zelditch, M.L., Swiderski, D.L., and Sheets, H. 2012. Geometric Morphometrics for Biologists: A Primer. Elsevier Academic Press, New York. https://doi.org/10.1016/b978-0-12-778460-1.x5000-5
