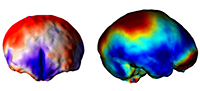
Surfin’ endocasts: The good and the bad on brain form
Article number: 21.1.1A
https://doi.org/10.26879/805
Copyright Palaeontological Association, January 2018
Author biographies
Plain-language and multi-lingual abstracts
PDF version
Submission: 14 July 2017. Acceptance: 20 December 2017
{flike id=2101}
ABSTRACT
Digital anatomy and computed morphometrics currently represent basic tools in anthropology, zoology, and paleontology. Despite the user-friendly interfaces of the programs, these methods require a robust expertise in statistics, biomedical imaging, and computer graphics. Geometrical modeling is aimed at normalizing shape variation as to compare forms within a shared reference space. As any other modeling approach, it can be used to test hypotheses or to investigate the structure of sample variation. In both cases, models refer to specific variables and parameters, and they follow numerical criteria that are based on algebraic and conventional rules. If models are interpreted too broadly and confused with the real anatomical elements, conclusions can be seriously biased. This risk can be particularly relevant when dealing with morphometric methods that do not use anatomical references, like sliding landmarks, surface analysis, or voxel-based morphometry. All these techniques are largely employed in craniology, paleoneurology, and evolutionary neuroanatomy. Following these approaches, elements are analyzed as “objects” and not as “anatomical elements,” introducing noise and drawbacks due to the registration processes and to the absence of constraints associated with anatomical boundaries. Downsides can be avoided by interpreting geometric models as specific representations of a set of properties of the original anatomical systems and not as generalized effigy of biological elements.
Emiliano Bruner. Grupo de Paleobiología, Centro Nacional de Investigación sobre la Evolución Humana, Paseo Sierra de Atapuerca 3, 09002 Burgos, Spain. emiliano.bruner@cenieh.es
Naomichi Ogihara. Faculty of Science and Technology, Department of Mechanical Engineering, Keio University, Yokohama, Kanagawa 223-8522, Japan. ogihara@mech.keio.ac.jp
Keywords: paleoneurology; morphometrics; shape analysis; surface analysis
Final citation: Bruner, Emiliano and Ogihara, Naomichi. 2018. Surfin’ endocasts: The good and the bad on brain form. Palaeontologia Electronica 21.1.1A: 1-10. https://doi.org/10.26879/805
palaeo-electronica.org/content/2018/2101-surface-and-form-analysis
Copyright: January 2018 Palaeontology Association.
This is an open access article distributed under the terms of Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0), which permits users to copy and redistribute the material in any medium or format, provided it is not used for commercial purposes and the original author and source are credited, with indications if any changes are made.
creativecommons.org/licenses/by-nc-sa/4.0/
SHAPING ANATOMY
In the last 20 years, morphometrics has undergone a dramatic development, thanks to computer-based anatomy and statistics. All anatomical fields have been particularly enhanced by such methods and tools, although paleontology (and particularly paleoanthropology) was especially rewarded by the advent of these informatic techniques (Zollikofer and Ponce de León, 2005; Gunz et al., 2009; Weber, 2015). Shape analysis was a major component of such epistemological change, mostly when considering landmark-based approaches, coordinates, superimposition methods, and multivariate statistics (Bookstein, 1991; Rohlf and Marcus, 1993; Adams et al., 2004; Slice, 2007; Mitteroecker and Gunz, 2009). The multivariate analysis of coordinates after spatial superimposition is generally named geometric morphometrics, a field which has experienced a remarkable development in the last two decades (Zelditch et al., 2004). Landmark-based analyses depend on the possibility to localize anatomical points, which must have a set of specific properties. They must have a biological meaning, have a reliable spatial position associated with a finite and punctual location, be present in all the specimens of a sample, be homologous in terms of phylogeny and development, and be associated with stable and rigid anatomical elements. It is apparent that only a limited number of anatomical regions and organs satisfy all these requisites, and it is easy to understand why these methods have been mostly employed to analyze cranial morphology (e.g., Lieberman et al., 2002; Zollikofer and Ponce de León, 2002; Bookstein et al., 2003). Landmark methods were soon also applied to neuroanatomy (Free et al., 2001) and especially to paleoneurology (Bruner et al., 2003; Bruner, 2004), a field that relies on casts of the endocranial cavity in fossil specimens and extinct species to make inferences on brain evolution. Endocranial casts (named “endocasts”) can’t supply information concerning internal brain changes, or aspects other than morphology and macroanatomy, but are useful to evaluate brain size and shape, cortical folding patterns, general brain proportions, and brain-skull spatial relationships (Neubauer, 2014; Bruner, 2015, 2017; Ogihara et al., 2015).
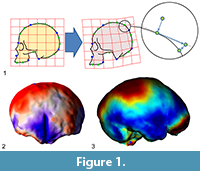Many surveys have been using geometric morphometrics to analyze brain morphology (e.g., Bruner et al., 2010, 2014; Gómez-Robles et al., 2013, 2014), but the elusive brain form is particularly void of fixed anatomical references, a limitation which seriously hampers a comprehensive analysis of its shape variations (Gómez-Robles et al., 2018; Pereira-Pedro and Bruner, 2018). The brain is made of soft tissues, and hence it lacks its “own form”. Its geometry is the result of an inner pressure exerted by blood, and an external tension exerted by the connective tissues attached to the cranial bones. The main macroscopical elements of the cortex are folds, which display an outstanding variation among individuals, which present blurred surfaces and boundaries, and whose associations in terms of functions, ontogeny, or morphogenesis are not known (Van Essen and Dierker, 2007). Because of these limitations, many surveys in evolutionary neuroanatomy have employed a different perspective, trying to escape the conceptual constraints of “anatomical landmarks” (Figure 1).
A first advance was achieved by introducing the so-called “sliding landmarks” (see Bookstein, 1997; Gunz et al., 2005; Perez et al., 2006; Gunz and Mitteroecker, 2013; Ogihara et al. 2014). In this case, landmarks are positioned evenly along a surface or curve, and then superimposed minimizing some algebraic criterion such as spatial distance (Procrustes distance) or spatial deformation (Bending Energy) among corresponding points, allowing their tangential displacement (“sliding”) constrained by the neighboring elements. The introduction of sliding landmarks notably enhanced the geometric morphometric toolkit, with crucial applications in paleoneurology (Neubauer et al., 2009, 2010; Gunz et al., 2010; Ponce de León et al., 2016). A second advance was based not on landmarks but on surfaces, by comparing the overall geometry of 3D objects using different criteria, registration procedures, and numerical approaches (e.g., Specht et al., 2007; Durrleman et al., 2012; Beaudet et al., 2016; Dupej et al., 2018). Sliding landmarks and surface analysis allow a finer geometric modeling of the anatomical forms, extending the resolution and applicability of form morphometrics, mostly in those fields (like paleoneurology) in which the anatomical elements are particularly void of consistent spatial references.
Nonetheless, the mathematics behind these computed approaches is indeed complex and extensive, requiring many operational passages and numerical transformations. This is not a problem when the final results are interpreted as the output of a numerical modeling that is a numerical simulation, which represents some qualities of the original anatomical system (position, spatial relationships etc.) according to specific algebraic procedures. Conversely, it may generate important bias when interpreting these models as a true corresponding representation of the real anatomical elements. Frequently, in the name of fluency, the term “endocranial cast” or “brain spatial model” is substituted for “brain”, and this may lead to stringent statements or generalized conclusions, which tend to confound the rough numerical results with a strict anatomical meaning.
SLIDING BRAINS
Analyses that are not based on homologous landmarks have two main limitations. The first one regards the amount of algebraic transformation required for these kinds of techniques. Any step is based on registration passages and algorithms, which implies a large chain of crucial methodological choices. The final result is an “ordination” of the original variables (coordinates), which should grant a proper correspondence between forms and areas, but which is sensitive to many operational issues. For example, when dealing with sliding landmarks, different sliding criteria can give different results (Bruner and Bastir, 2009), and attention must be paid when deciding between the available operational alternatives. Procrustes distances are influenced by local variation, while bending energy is responsive to more global changes (Gunz and Mitteroecker, 2013). Every registration procedure can be biased by an uneven distribution of the differences and/or uneven distribution of landmarks (Richtsmeier et al., 2002), but in these cases the risks are even larger, because of the lack of strict anatomical correspondences between spatial units (landmarks or pixels) and their supposed anatomical background. Therefore, when we introduce additional transformations, we are introducing more operational steps within the chain of numerical adjustments, increasing the separation between the rough data and their final synthetic representations. For surface analyses this chain is definitely much larger than for sliding landmarks, and the list of steps which are sensitive to possible biases, errors, or numerical constraints, is much longer. Only a very small percentage of morphometricians (and an even lower percentage of journal readers in general) are competent in all the aspects required to control this dense mathematical background, and hence capable of a full and critical comprehension of the numerical adjustments involved. This limitation is even more significant when considering that in the current scientific literature, the description of such methods is more and more relegated to secondary supplementary online materials, and often ignored by the general readership. All this methodological development has empowered analytical capacity, but it has also incremented pitfalls and drawbacks, which require caution and a constant technological verification from the community.
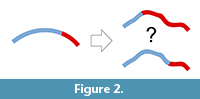A second limit is inherent to this kind of data. Both approaches (most of all surface analyses) rely on geometric correspondence and not on anatomical correspondence. Geometric correspondence is a good criterion to analyze a 3D object, but implicitly it cannot provide information on anatomical boundaries and proportions. That is, the object is analyzed as “an object”, and not as “a skull” or as “a brain”. Of course, this is true for whatever registration approach (Richtsmeier et al., 2002), but in the case of surfaces or outlines the model is further disconnected from local features of the anatomical system. Spatial variations of the object are then “spread” over the whole surface, and this involves two main consequences. First, there will be a loss of information, because the absence of specific anatomical boundaries will hide local differences (Figure 2). Namely, if we analyze the morphology of distinct anatomical areas together, the final results will depend on an admixture of independent factors, ignoring the respective contributions of the different parts. This is a limitation, but not a bias, when opportunely taken into consideration. The same uncertainty can be observed any time one analyzes pooled variables (including size or volumes) of different anatomical districts. For example, dealing with traditional volumetric comparisons, Semendeferi and Damasio (2000) found a proportional variation of the parieto-occipital cortical block among apes, including humans. They analyzed together the parietal and occipital lobes because of difficulties in separating the two districts, and then properly limited their conclusions to the parieto-occipital block. Nonetheless, many papers subsequently citing that study inappropriately mentioned that allometric analyses had demonstrated constant proportions in the parietal “and” in the occipital lobes. The fact that humans have a reduced primary visual cortex (De Sousa et al., 2010) suggests that the lack of change in the overall parieto-occipital proportions might be instead a hybrid result of increase of the parietal cortex and decrease of the occipital one. A pooled analysis of the parieto-occipital block masks the distinct contributions of the two elements. When dealing with shape instead of volume, the examples can be far more complex and subtle.
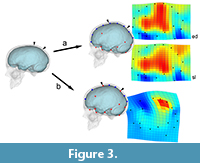The second consequence of grouping different elements in morphometric surveys may be more influent, mostly when dealing with shape analysis and registration procedures: without boundaries, shape variation will be equally distributed through the whole spatial model, loading (and smoothing) local changes onto global changes, and artificially displacing the form differences (Figure 3). Namely, a change associated with a specific anatomical element or area will be interpreted as a more extensive and less pronounced morphological variation. In these cases, we have a loss of information but we also have a biased result, which wrongly assumes that all parts have equally contributed to the phenotypic differences. If we are only considering the covariation structure, this effect is less relevant, because the main target is to localize correlations and associations between coordinates, ordering the overall variation according to these hidden rules (Bruner, 2018). But then, when mapping these patterns on graphical anatomical models for visual purposes (as is usually done in geometric morphometrics or surface analysis), the result may be seriously misleading if interpreted too strictly. This is a generalization of the so-called “Pinocchio effect” (Walker, 2000; Klingenberg, 2013), that can bias the final conclusions of a study when semi-landmarks and surface analysis are applied without taking into account the existence of actual anatomical boundaries, particularly on an “object” (the brain) which has an extremely complex topological organization (Glasser et al., 2016).
MODELING EVOLUTION
When distinct parts have different effects on the overall morphological difference, if they are analyzed together their relative contribution cannot be ruled out. Their influences can be artificially mixed, and different phenotypic processes can be confounded if local contributions cannot be properly taken into account. These consequences are proportional to the extent of the lack of anatomical boundaries. Namely, they will be more misleading in cases with few anatomical landmarks and many semi-landmarks, and even extreme in surface analyses, which are generally based almost only on surface matching.
Such limitations of course should not be used to reject the contribution of these morphometric tools, which probably represent one of the major advances in this field in recent years. Quantitative outputs, like warping grids, color maps, or complex dendrograms, are but visual representations of mathematical relationships, as evidenced according to specific algebraic criteria. Thus, those outputs (which are but numerical results) should not be confused with a specific biological effect, or with a specific hypothesis. Instead, those outputs should be used to support or to reject some preceding hypothesis, which must be based on multiple and independent evidence. In absence of a specific hypothesis, geometric modeling is also useful to investigate and “explore” the multivariate structure of a given anatomical variation (Bruner, 2018). However, in this case, conclusions must be based on the actual signal associated with the numerical modeling. That is, results must be interpreted within their methodological constraints, avoiding generalized inferences that go beyond the actual range of the study. A bunch of pixels or a covariance matrix are digital and numerical representations of some properties of a brain, and should not be confounded with the brain itself.
Apart from a proper interpretation of the results, shape analysis in neuroanatomy and paleoneurology should be improved at least in three ways. First, anatomical and homologous landmarks should be included in landmark-based approaches, so as to “anchor” variation according to local changes of real anatomical elements. Second, more information on folding schemes and cortical biology is necessary. The noticeable individual variation of the cortical surface and the lack of a proper knowledge on its functional meaning often hamper a reliable use of cortical landmarks. Cortical variations could be the result of geometrical relationships (Hofman, 2014), connectivity patterns (Van Essen, 1997), and biomechanical constraints (Tallinen et al., 2016). In any case, the scarce information available on variations and the mechanisms of cortical folding is still limiting the application of shape analysis in many brain districts. Third, most of all in paleoneurology, more information on the spatial and morphogenetic relationships between skull and brain can surely add to provide more robust neuroanatomical inferences on extinct species (Pearce et al., 2013; Kobayashi et al., 2014a; Kochiyama et al., 2018). The spatial relationships between brain and braincase can reveal some useful correlations between soft and hard tissues, and quantify the degree of association and reliability between cranial and cortical areas (Kobayashi et al., 2014b; Bruner et al., 2015).
As further cautionary note, it is worth noting that many brain and cranial anatomical traits display a remarkable intra-specific variation, and at the same time minor or subtle inter-specific mean differences. Therefore, large samples are generally required to provide consistent numerical results, able to identify and test, with a proper statistical power, group similarities, or, conversely, distinct patterns. Such large samples, in general, are not available when working with the human fossil record. Accordingly, analyses based on few individuals (or even single specimens) can be central in some cases, but should not be regarded as conclusive.
A final note concerns the use of registration approaches and surface-based analyses to compare brain volumes and parcellations in different groups or subjects, according to standardized atlases and spatial references (Van Essen and Dierker, 2007). While in morphometrics, algorithms and deformation fields are generally used to reveal differences, when working with brain mapping the same numerical transformations are used to eliminate differences, registering the specimens within a shared space (Ashburner and Friston, 2000). Rigid and non-rigid transformations are used to minimize the differences among individuals, so making them comparable within the same system of coordinates. Such transformation is necessary to deal with the considerable inter-individual anatomical and functional variability associated with brain anatomy. In this case, two limitations must be taken into account. The first one is once more associated with the reliability of the large chain of numerical transformation used in these kinds of approaches. Results will depend on the algorithms employed, on the template used as a reference, and on a large set of constraints introduced in the registration process. Therefore, results will be “true” only according to those specific operational and numerical criteria, and are sensitive to many possible bias and mistakes (Gronenschild et al., 2012). The second limitation is due to the principles behind the registration procedures that, in general, are based on spatial information and not on anatomical information. For example, the widely used voxel-based morphometry is a voxel-to-voxel statistic of the grayscale values after registration of brain images within the same spatial framework. This technique is extremely useful to compare global differences in terms of quantitative signals (the proportions and spatial distribution of the grayscale values), but the correspondence between the original and registered morphology is lost. In fact, registration deforms the original images by shrinking and expanding local topology. This normalization, essential to perform population-based mapping and cortical cartography, represents a bias when the final target is a morphometric (form and shape) analysis of the brain districts. All these limitations are part of the method, and they are perfectly acknowledged in the general outlines of these techniques (see Ashburner and Friston, 2000, 2001; Van Essen and Dierker, 2007). Nonetheless, they are often neglected in many specific surveys, when dealing with specific case-studies or with more heuristic explorations.
All these techniques represent a real revolution in neuroanatomy and morphometrics. Nevertheless, such analytical power can introduce major bias when it is not used properly. The more the power, the more the effect can be influential. And, of course, a methodology is not necessarily good or conclusive simply because it is complex or pioneering. Most of these analytical tools and procedures are based on very large operational chains made of assumptions, criteria, and technological devices, which cannot be properly described or verified in every published paper. In all these cases, methods largely rely on citations and previous literature, so requiring a sort of trust and reliance on their efficiency. Caution is required, and competence is the only warranty we have to exploit the exceptional potentialities of these tools, reducing the drawbacks of their limitations.
ACKNOWLEDGMENTS
We are grateful to M. Bastir, A. Gómez-Robles, P. Gunz, A. Beaudet, J. Dupej, O. Kondo and H. Amano for the many debates and collaborations on the topics discussed in this article. This paper has been designed within the Grant-in-Aid for Scientific Research on Innovative Areas “Replacement of Neanderthals by Modern Humans: Testing Evolutionary Models of Learning” from the Japanese Ministry of Education, Culture, Sports, Science, and Technology (#22101006). EB is funded by the Spanish Government (CGL2015-65387-C3-3-P).
REFERENCES
Adams, D.C., Rohlf, F.J., and Slice, D.E. 2004. Geometric morphometrics: ten years of progress following the “revolution.” Italian Journal of Zoology, 71:5-16. https://doi.org/10.1080/11250000409356545
Ashburner, J. and Friston, K.J. 2000. Voxel-based morphometry - The methods. NeuroImage, 11:805-821. https://doi.org/10.1006/nimg.2000.0582
Ashburner, J. and Friston, K.J. 2001. Why voxel-based morphometry should be used. NeuroImage, 14:1238-1243. https://doi.org/10.1006/nimg.2001.0961
Beaudet, A. and Bruner, E. 2017. A frontal lobe surface analysis in three archaic African human fossils: OH 9, Buia, and Bodo. Comptes Rendus Palevol, 16:499-507. https://doi.org /10.1016/j.crpv.2016.12.002
Beaudet, A., Dumoncel, J., de Beer, F., Duployer, B., Durrleman, S., Gilissen, E., Hoffman J., Tenailleau C., Thackeray J.F., Braga J. 2016. Morphoarchitectural variation in South African fossil cercopithecoid endocasts. Journal of Human Evolution, 101: 65-78. https://doi.org/10.1016/j.jhevol.2016.09.003
Bookstein, F.L. 1991. Morphometric Tools for Landmark Data. Cambridge University Press, New York.
Bookstein, F.L. 1997. Landmark methods for forms without landmarks: morphometrics of group differences in outline shape. Medical Image Analysis, 1:225-243.
Bookstein, F.L., Gunz, P., Mitteroecker P., Prossinger, H., Schaefer, K., and Seidler, H. 2003. Cranial integration in Homo: singular warps analysis of the midsagittal plane in ontogeny and evolution. Journal of Human Evolution, 44:167-187. https://doi.org/10.1016/S0047-2484(02)00201-4
Bruner, E. 2004. Geometric morphometrics and paleoneurology: brain shape evolution in the genus Homo. Journal of Human Evolution, 47:279-303. https://doi.org/10.1016/j.jhevol.2004.03.009
Bruner, E. 2015. Functional craniology and brain evolution, p. 57-94. In Bruner, E. (ed.), Human Paleoneurology. Springer, Switzerland.
Bruner E. 2017. The fossil evidence of human brain evolution, p. 63-92. In Kaas, J. (ed.), Evolution of Nervous Systems 2e, vol. 4. Elsevier, Oxford.
Bruner, E. 2018. The brain, the braincase, and the morphospace (in press). In Bruner, E., Ogihara, N., and Tanabe, H. (eds.), Digital Endocasts. Springer, Japan.
Bruner, E. and Bastir, M. 2009. Landmarks could slide, brains can not: interpreting models of shape variation. Paleontologia I Evolució, Memòria Especial, Institut Catalá de Paleontologia, Barcelona, 3:33.
Bruner, E., Manzi, G., and Arsuaga, J.L. 2003. Encephalization and allometric trajectories in the genus Homo: evidence from the Neandertal and modern lineages. Proceedings of the National Academy of Science, USA, 100:15335-15340. https://doi.org/10.1073/pnas.2536671100
Bruner, E., Martin-Loeches, M., and Colom, R. 2010. Human midsagittal brain shape variation: patterns, allometry and integration. Journal of Anatomy, 216:589-599. https://doi.org/10.1111/j.1469-7580.2010.01221.x
Bruner, E., Rangel de Lázaro, G., de la Cuétara, J.M., Martín-Loeches, M., Colóm, R., and Jacobs, H.I.L. 2014. Midsagittal brain variation and MRI shape analysis of the precuneus in adult individuals. Journal of Anatomy, 224:367-376. https://doi.org/10.1111/joa.12155
Bruner, E., Amano, H., de la Cuétara, J.M., and Ogihara, N. 2015. The brain and the braincase: a spatial analysis on the midsagittal profile in adult humans. Journal of Anatomy, 227:268-276.
De Sousa, A.A., Sherwood, C.C., Mohlberg, H., Amunts, K., Schleicher, A., MacLeod, C.E., Hof P.R., Frahm, H., Zilles, K. 2010. Hominoid visual brain structure volumes and the position of the lunate sulcus. Journal of Human Evolution, 58:281-292. https://doi.org/10.1016/j.jhevol.2009.11.011
Dupej, J., Rangel de Lázaro, G., Pereira-Pedro, S., Píšová, H., Pelikán, J., and Bruner, E. 2018. Comparing endocranial surfaces: mesh superimposition and coherent point drift registration (in press). In Bruner, E., Ogihara, N., and Tanabe, H. (eds.), Digital Endocasts. Springer, Japan.
Durrleman, S., Pennec, X., Trouvé, A., Ayache, N., and Braga, J. 2012. Comparison of the endocranial ontogenies between chimpanzees and bonobos via temporal regression and spatiotemporal registration. Journal of Human Evolution, 62:74-88. https://doi.org/10.1016/j.jhevol.2011.10.004
Free, S.L., O’Higgins, P., Maudgil, D.D., Dryden, I.L., Lemieux, L., Fish, D.R., and Shorvon, S.D. 2001. Landmark-based morphometrics of the normal adult brain using MRI. NeuroImage, 13:801-813. https://doi.org/10.1006/nimg.2001.0748
Glasser, M.F., Coalson, T.S., Robinson, E.C., Hacker, C.D., Harwell, J., Yacoub, E., Ugurbil, K., Andersson, J., Beckmann, C.F., Jenkinson, M., Smith, S.M., Van Essen, D.C. 2016. A multi-modal parcellation of human cerebral cortex. Nature, 536:171-178. https://doi.org/10.1038/nature18933
Gómez-Robles, A., Hopkins, W.D., and Sherwood, C.C. 2013. Increased morphological asymmetry, evolvability and plasticity in human brain evolution. Proceedings of the Royal Society B, 280:20130575. https://doi.org/10.1098/rspb.2013.0575
Gómez-Robles, A., Hopkins, W.D., and Sherwood, C.C. 2014. Modular structure facilitates mosaic evolution of the brain in chimpanzees and humans. Nature Communications, 5:4439. https://doi.org/10.1038/ncomms5469
Gómez-Robles, A., Reyes, L.D., and Sherwood, C.C. 2018. Landmarking brains (in press). In Bruner, E., Ogihara, N., and Tanabe, H. (eds.), Digital Endocasts. Springer, Japan.
Gronenschild, E.H., Habets, P., Jacobs, H.I., Mengelers, R., Rozendaal, N., van Os, J., and Marcelis, M. 2012. The effects of FreeSurfer version, workstation type, and Macintosh operating system version on anatomical volume and cortical thickness measurements. PLoS ONE, 7:e38234. https://doi.org/10.1371/journal.pone.0038234
Gunz, P. and Mitteroecker, P. 2013. Semilandmarks: a method for quantifying curves and surfaces. Hystrix, 24:103-109. https://doi.org/10.4404/hystrix-24.1-6292
Gunz, P., Mitteroecker, P., and Bookstein, F.L. 2005. Semilandmarks in three dimensions, p. 73-98. In Slice, D.E. (ed.), Modern Morphometrics in Physical Anthropology. Kluwer Academic/Plenum Publishers, New York.
Gunz, P., Mitteroecker, P., Neubauer, S., Weber, G.W., and Bookstein, F.L. 2009. Principles for the virtual reconstruction of hominin crania. Journal of Human Evolution, 57:48-62. https://doi.org/10.1016/j.jhevol.2009.04.004
Gunz, P., Neubauer, S., Maureille, B., and Hublin, J.J. 2010. Brain development after birth differs between Neanderthals and modern humans. Current Biology, 20:R921-R922. https://doi.org/10.1016/j.cub.2010.10.018
Hammer, Ø., Ryan, P., and Harper, D. 2001. PAST: Paleontological Statistics software package for education and data analysis. Palaeontologia Electronica, 4.1.4:1-9.
http://palaeo-electronica.org/2001_1/past/issue1_01.htm
Hofman, M.A. 2014. Evolution of the human brain: when bigger is better. Frontiers in Neuroanatomy, 8:15. https://doi.org/10.3389/fnana.2014.00015
Klingenberg, C.P. 2013. Cranial integration and modularity: insights into evolution and development from morphometric data. Hystrix, 24:43-58. https://doi.org/10.4404/hystrix-24.1-6367
Kobayashi, Y., Matsui, T., Haizuka, Y., Hirai, N., and Matsumura, G. 2014a. Cerebral sulci and gyri observed on macaque endocasts, p. 131-137. In Akazawa, T., Ogihara, N., Tanabe, H., and Terashima, H. (eds.), Dynamics of Learning in Neanderthals and Modern Humans, Volume 2. Springer, Japan.
Kobayashi, Y., Matsui, T., Haizuka, Y., Hirai, N., and Matsumura, G. 2014b. The coronal suture as an indicator of the caudal border of the macaque monkey prefrontal cortex, p. 139-143. In Akazawa, T., Ogihara, N., Tanabe, H., and Terashima, H. (eds.), Dynamics of Learning in Neanderthals and Modern Humans, Volume 2. Springer, Japan.
Kochiyama, T., Tanabe, H.C., and Ogihara, N. 2018. Reconstruction and statistical evaluation of fossil brains using computational neuroanatomy (in press). In Bruner, E., Ogihara, N., and Tanabe, H. (eds.), Digital Endocasts. Springer, Japan.
Lieberman, D.E, McBratney, B.M., and Krovitz, G. 2002. The evolution and development of cranial form in Homo sapiens. Proceedings of the National Academy of Science, USA, 99:1134-1139. https://doi.org/10.1073/pnas.022440799
Mitteroecker, P. and Gunz, P. 2009. Advances in geometric morphometrics. Evolutionary Biology, 36:235-247. https://doi.org/10.1007/s11692-009-9055-x
Neubauer, S. 2014. Endocasts: possibilities and limitations for the interpretation of human brain evolution. Brain Behavior and Evolution, 84:117-134. https://doi.org/10.1159/000365276
Neubauer, S., Gunz, P., and Hublin, J.J. 2009. The pattern of endocranial ontogenetic shape changes in humans. Journal of Anatomy, 215:240-255. https://doi.org/10.1111/j.1469-7580.2009.01106.x
Neubauer, S., Gunz, P., and Hublin, J.J. 2010. Endocranial shape changes during growth in chimpanzees and humans: a morphometric analysis of unique and shared aspects. Journal of Human Evolution, 59:555-566. https://doi.org/10.1016/j.jhevol.2010.06.011
Ogihara, N., Amano, H., Kikuchi, T., Morita, Y., Hasegawa, K., Kochiyama, T., and Tanabe, H.C. 2015. Towards digital reconstruction of fossil crania and brain morphology, Anthropological Science, 123:57-68. https://doi.org/10.1537/ase.141109
Ogihara, N., Morita, Y., Amano, H., Kondo, O., Suzuki, H., and Nakatsukasa, M. 2014. Application of sliding landmark method for morphological analysis of modern Japanese neurocranial shape, p. 145-152. In Akazawa, T., Ogihara, N., Tanabe, H., and Terashima, H. (eds.), Dynamics of Learning in Neanderthals and Modern Humans, Volume 2. Springer, Japan.
Pearce, E., Stringer, C., and Dunbar, R.I.M. 2013. New insights into differences in brain organization between Neanderthals and anatomically modern humans. Proceedings of the Royal Society B, 280:20130168. https://doi.org/10.1098/rspb.2013.0168
Pereira-Pedro, S. and Bruner, E. 2018. Landmarking endocast (in press). In Bruner, E., Ogihara, N., and Tanabe, H. (eds.), Digital Endocasts. Springer, Japan.
Perez, S.I., Bernal, V., and Gonzalez, P.N. 2006. Differences between sliding semi-landmark methods in geometric morphometrics, with an application to human craniofacial and dental variation. Journal of Anatomy, 208:769-784. https://doi.org/10.1111/j.1469-7580.2006.00576.x
Ponce de León, M.S., Bienvenu, T., Akazawa, T., and Zollikofer, C.P.E. 2016. Brain development is similar in Neanderthals and modern humans. Current Biology, 26:R665-R666. https://doi.org/10.1016/j.cub.2016.06.022
Richtsmeier, J.T., DeLeon, V.B., and Lele, S.R. 2002. The promise of geometric morphometrics. American Journal of Physical Anthropology, S35:63-91. https://doi.org/10.1002/ajpa.10174
Rohlf, F.J. and Marcus, L.F. 1993. A revolution in morphometrics. Trends in Ecology and Evolution, 8:129-132. https://doi.org/10.1016/0169-5347(93)90024-J
Semendeferi K. and Damasio H. 2000. The brain and its main anatomical subdivisions in living hominoids using magnetic resonance imaging. Journal of Human Evolution, 38:317-332. https://doi.org/10.1006/jhev.1999.0381
Slice, D.E. 2007. Geometric morphometrics. Annual Review of Anthropology, 36:261-281. https://doi.org/10.1146/annurev.anthro.34.081804.120613
Specht, M., Lebrun, R., and Zollikofer, C.P.E. 2007. Visualizing shape transformation between chimpanzee and human braincases. Visual Computer, 23:743-751. https://doi.org/10.1007/s00371-007-0156-1
Tallinen, T., Chung, J.Y., Rousseau, F., Girard, N., Lefèvre, J., and Mahadevan, L. 2016. On the growth and form of cortical convolutions. Nature Physics, 12:588-593. https://doi.org/10.1038/nphys3632
Van Essen, D.C. 1997. A tension-based theory of morphogenesis and compact wiring in the central nervous system. Nature, 385:313-318. https://doi.org/10.1038/385313a0
Van Essen, D.C. and Dierker D.L. 2007. Surface-based and probabilistic atlases of primate cerebral cortex. Neuron, 56:209-225. https://doi.org/10.1016/j.neuron.2007.10.015
Walker, J.A. 2000. Ability of geometric morphometric methods to estimate a known covariance matrix. Systematic Biology, 49:686-696.
Weber, G.W. 2015. Virtual anthropology. American Journal of Physical Anthropology, 156:22-42. https://doi.org/10.1002/ajpa.22658
Zelditch, M.L., Swidersky, D.L., Sheets, H.D., and Fink, W.L. 2004. Geometric Morphometrics for Biologists. Elsevier, San Diego.
Zollikofer, C.P.E. and Ponce de León, M. 2002. Visualizing patterns of craniofacial shape variation in Homo sapiens. Proceedings of the Royal Society B, 269:801-807. https://doi.org/10.1098/rspb.2002.1960
Zollikofer, C.P.E. and Ponce de León, M.S. 2005. Virtual Reconstruction: A Primer in Computer-Assisted Paleontology and Biomedicine. Wiley-Liss, New York.
