GM in ammonoids OBM vs VMM

Comparative assessment of outline-based vs. virtual modeling-based methods to analyze the ammonoid whorl profile

Daniel A. Morón-Alfonso, Ninon Allaire, and Samuel Ginot

Article number: 27.3.a53
https://doi.org/10.26879/1369
Copyright Palaeontological Association, November 2024

Author biographies
Plain-language and multi-lingual abstracts
PDF version
Appendices

Submission: 15 January 2024. Acceptance: 17 October 2024.

ABSTRACT

In this report we compare two geometric morphometric methods (Outline-based vs. Virtual Modeling-based) aiming to analyze the ammonoid whorl profile shape (designated as whorl cross-section shape in previous contributions). A dataset including 50 ammonoid whorl profiles is used to evaluate the two approaches, and the resulting morphospaces are compared. The morphological variations depicted by PC1 and PC2 are consistent across methods and are congruent with previously reported patterns (the predicted morphologies are similar). PC1 captures from 66% to 70% of the total variance; along this axis the morphological transformation is mainly associated with the degree of conch compression. For PC2 the variation is associated with the elongation/compression of the whorl profile, and with the relative height of the imprint zone (degree of whorl overlap). The variation summarized across the first two principal components is about 88% for the Virtual Modeling Method (VMM) and about 94% for the Outline-based Method (OBM). The principal differences between the two approaches lie in the way they quantify the imprint zone. The transformations associated with the shape of this region are related to PC3 and are more specifically linked to the shape and lateral dimensions of the umbilical walls. VMM allows a more accurate quantification of the imprint zone shape, while OBM shows more limited performances for quantifying this specific zone of the whorl profile.

Daniel A. Morón-Alfonso. Universidad de Buenos Aires, Facultad de Ciencias Exactas y Naturales, Departamento de Ciencias Geológicas, Área de Paleontología, Ciudad Universitaria, Pab. 2, C1428EGA, Buenos Aires, Argentina. CONICET-Universidad de Buenos Aires, Instituto de Estudios Andinos “Don Pablo Groeber” (IDEAN), Buenos Aires, Argentina. paleokarzis@gmail.com
Ninon Allaire. Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), Centro de Investigaciones en Ciencias de la Tierra (CICTERRA), Córdoba, Argentina. ninon.allaire@gmail.com
Samuel Ginot. Bonner Institut für Organismische Biologie, Universität Bonn, An der Immenburg 1, 53121 Bonn, Germany. ginotsam@gmail.com

Keywords: geometric; morphometrics; ammonoid; landmarks; semi-landmarks; outline; ammonite

Final citation: Morón-Alfonso, Daniel A., Allaire, Ninon, and Ginot, Samuel. 2024. Comparative assessment of outline-based vs. virtual modeling-based methods to analyze the ammonoid whorl profile. Palaeontologia Electronica, 27(3):a53.
https://doi.org/10.26879/1369
palaeo-electronica.org/content/2024/5365-gm-in-ammonoids-obm-vs-vmm

Copyright: November 2024 Palaeontological Association.
This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
creativecommons.org/licenses/by/4.0

INTRODUCTION

Geometric morphometrics (GM) is one of the most widely applied methodologies for studying the shape of biological structures in both extant and extinct organisms (Adams et al., 2004; Mitteroecker and Schaefer, 2022). GM summarize the geometry of an object by employing a set of landmarks, curves, or surfaces, that are then transformed enabling their analysis through various multivariate methods. The application of GM addresses many limitations of traditional morphometrics, including the difficulties in distinguishing form and shape geometric variation (i.e., in the context of GM, shape = form + size), of comparing complex irregular shapes, and the lack of independence among linear dimensions (Mitteroecker and Schaefer, 2022). Adams et al. (2004) proposed a classification of GM methods, into two principal approaches: Landmark-based and Outline-based methods. The former describes anatomical features using sets of two- or three-dimensional coordinates (configurations) that are subsequently superimposed, usually using Procrustes Analysis (standardizing the scale, size, and relative location). The results of this procedure can be further analyzed using Principal Component Analysis (PCA) to build a morphospace that facilitates comparisons, illustrates the main transformations, and relative relationships between the studied configurations. In contrast, for Outline-based methods the standard approach involves digitizing points along an outline and fitting these points with a mathematical function--commonly a form of Fourier analysis-- followed by the comparison of the curves using the coefficients of these functions as shape variables in multivariate analyses (including PCA).

Normally, landmark-based methods are preferred when the definition of homologous points in the sample is feasible. On the contrary, outline-based methods are more suitable when these conditions are not met, often exhibited in cases addressing rounded shapes or structures characterized by multiple curves. It should be noted that, in addition to these GM methods, nowadays there are several alternatives, including: different ways of superimposing landmarks configurations, the definition of sliding landmarks (semi-landmarks) to define curves, among many other variations (Adams et al., 2013; Mitteroecker and Schaefer, 2022).

GM methods have been extensively applied in ammonoids. This is an extinct group of cephalopods that retained an external shell during all its evolutionary history from the early Devonian up to the end of the Cretaceous, surviving briefly across the Cretaceous/Paleogene limit (Machalski and Heinberg, 2005; Landman et al., 2012; Klug et al., 2015a). Fossils of this external conch represent one of the most common findings in marine assemblages, showing a highly diverse and abundant record around the world (Saunders and Swan, 1984; Dommergues et al., 1996; Saunders et al., 2004; Korn and Klug, 2012; Monnet et al., 2015; Morón-Alfonso et al., 2023, figs. 3-4). Because the ammonoid conch grew along with the animal soft body, this structure frequently records valuable information including morphological modifications that occurred during ontogeny (Kullmann and Scheuch, 1970; Kant, 1973; Korn, 2012; Korn and Klug, 2012; Erlich et al., 2016). According to Tajika and Klug (2020) the most effective method for investigating morphological transformations involves extracting transversal cross-sections of the conch at 30° steps or lower, usually obtained from tomographic datasets. However, it’s pertinent to note that despite its perceived precision, this approach is uncommon. Instead, researchers often opt for the more accessible and less time-consuming 180° step method, often utilizing polished sections through the center. In general, data extracted from these procedures are plotted as ontogenetic trajectories that illustrate the variation of either a morphological parameter or another informative variable (e.g., septal spacing) against a size proxy (Ebbighausen and Korn, 2007; Korn, 2010; Klug et al., 2015b). A similar analytical approach can be applied using GM, focusing on the variation of the whorl profile (i.e., the shape of the whorl in a cross-section of the conch). In this context, both landmark-based and outline-based methods have been applied in ammonoid studies (e.g., Neige, 1999; Allen, 2007; Korn and Klug, 2012; Klein and Korn, 2014; Courville and Crônier, 2016; Wegerer et al., 2018; Bischof and Lehmann, 2020; Bischof et al., 2021).

In previous contributions (Morón-Alfonso et al., 2021; 2023), we introduced a method wherein virtual models are transformed into semi-landmarks utilizing a subdivision surface algorithm referred here as Virtual Modeling Method (VMM). The semi-landmark configurations obtained from this procedure can be evaluated following a Landmark-based approach. This methodology was applied to examine the whorl profile of a sample comprising 300 ammonoid genera. The resulting morphospace structure exhibits similarities with the one obtained by Allaire et al. (2023) that used an alternative outline-based method, relying on Fourier analysis (designed hereafter by OBM). However, a formal comparison between these approaches (VMM versus OBM) has not been presented to date, so these common patterns are still poorly understood. In this study, employing a random sample of whorl profiles representing 50 ammonoid genera, we scrutinize the differences and similarities between these two methodologies. We explore their resulting morphospaces and the transformations resumed by their principal components. Additionally, we introduce innovations to VMM, incorporating more complex configurations (up to 56 semi-landmarks). These modifications are applied to the available datasets to reanalyze previous results and consider further possible implications.

MATERIAL AND METHODS

Dataset

The sample utilized in this study represents a subset of the dataset employed in Morón-Alfonso et al. (2023) featuring 300 whorl profiles representing different ammonoid genera ranging from the Devonian to the Cretaceous. This sample was compiled from the literature, photographs, and CT volumes available in multiple repositories: Colección de Paleontología de la Universidad de Buenos Aires (CPBA, Argentina), Colección de Paleoinvertebrados del Instituto Antártico Argentino (IAA-pi, Argentina), Colección de Paleontología del Museo José Royo y Gómez (RGM, Colombia), Ruhr-Universität Bochum Repository (RUB-Pal, Germany), The Digital Atlas of Ancient Life (virtual repository by Hendricks et al., 2015), Muséum National d’Histoire Naturelle (MNHN virtual Repository, France), GB3D Type Fossils Online (a virtual repository of the Oxford University Museum of Natural History, UK), and the Natural History Museum Dataset (2014, a virtual repository, UK). The dataset, along with its original references, is provided in Appendix 1.

The subset employed in this work constitutes 50 randomly selected representatives from the original sample employing the Mersenne Twister algorithm (Gilli et al., 2019). This relatively low number of configurations is practical to determine the location of the taxa within the generated morphospaces, thus facilitating the comparisons between the different methods. A preliminary evaluation of this subset indicates that both the number and the location of the specimens, were appropriate to depict the general structure of the larger morphospace presented in Morón-Alfonso et al. (2023; see Appendix 2).

Analytical Methods

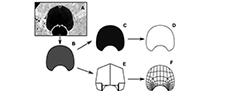
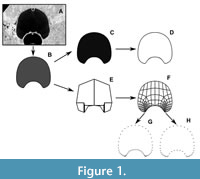The procedure corresponding to each method Outline Based Method (OBM) vs Virtual Model Method (VMM) is summarized in Figure 1. The original illustrations of the whorl profiles were translated into virtual models using the process detailed in Morón-Alfonso et al. (2021). This procedure was performed using Blender 4.0 (Blender Online Community, 2022); in this case, we employed two subdivisions to create the virtual models that were exported as 3D objects (.OBJ files) and further utilized to generate the necessary data (Figure 1A-B).

For the VMM method, the vertices were extracted from the virtual models and recorded in a text file (Figure 1F-H). Subsequently, a Python function (Vertex Extractor 0.0.1) was employed to isolate the vertices along the outline, which were subsequently compiled into separate files (Figure 1G; Appendix 2). Initially, this process yielded configurations comprising 56 semi-landmarks (SL). However, it was observed that the points in the imprint zone were disproportionately overrepresented compared to the rest of the whorl profile. This discrepancy arose from the subdivision of the vertices describing both the imprint zone and the umbilical walls from the original simplified model. In the simpler 18 SL configurations (Morón-Alfonso et al., 2021, 2023), the relatively low number of points defining this region may not significantly impact the results. However, with the multiplication of points, the results could vary for more complex models. To prevent potential biases resulting from this overrepresentation, adjustments were made to the configurations by subsampling the number of points associated with the conflicted area. The refinement resulted in a configuration of 44 semi-landmarks (Figure 1H; Appendix 2). Then, the configurations were standardized via Procrustes Analysis using the R package Morpho 2.11 (Schlager, 2020).

For the OBM, the virtual models were rendered as black and white silhouettes in Blender 4.0 (Figure 1C), and then translated to outlines using the R package Momocs 1.4.1 (Bonhomme et al., 2014). Subsequently, we followed the procedure described by Allaire et al. (2023), in which the outlines were converted into a sequence of 200 evenly distributed semi-landmarks (Figure 1D). These semi-landmarks were then superimposed using functions within the package, and the resultant coordinates were modeled into harmonic coefficients through elliptical Fourier analysis (Figure 1E). For this procedure, we employed six harmonics representing 99% of the cumulative Fourier harmonic power as was implemented in the original study.

In both cases, following the superimposition (and Fourier analysis for OBM), the resulting data was processed using Principal Component Analysis (PCA). The morphospaces obtained were compared, and the predicted configurations were illustrated to analyze the transformations summarized by each principal component. To accomplish this goal, ‘back-transforms’ of the morphospaces (Olsen, 2017) were generated using the R package Morphospace 0.0.1 (Milla Carmona, 2022). Further, the first three PCs for each setting were compared using simple Pearson correlation tests to assess the relationship between corresponding PCs. Additionally, Mantel tests were performed to compare the bidimensional (PC1 and PC2) and the three-dimensional (PC1, PC2, and PC3) morphospaces. These analyses were executed using the package Vegan 2.6.4 in R; the method selected was Spearman Correlation with 9999 permutations (see Appendix 2). Finally, two-block Partial Least Squares (PLS) analysis was employed to test correlations between matrices representing each multidimensional morphospace, using the function “two.b.pls” from the “geomorph” package v. 4.0.4 (Baken et al., 2021; Adams et al., 2022; Collyer and Adams, 2018; 2021), with P-values being computed based on 1000 permutations.

RESULTS

Here, we compiled the results for three distinct test settings: 1) VMM using 56 semi-landmarks (VMM 56-SL), 2) VMM using 44 semi-landmarks (VMM 44-SL), and 3) OBM. Table 1 summarizes the percentage of variation represented by each principal component for each setting. Table 2 shows the results of the Pearson correlation tests, Table 3 summarizes the results for the Mantel tests, and Table 4 displays the results for the two-block PLS analyses between pairs of multidimensional morphospaces. The scripts and the complementary illustrations for the VMM 44-SL setting are provided in Appendix 2. It is worth noting that the variation for PC1 is similar across methods, ranging from 66% to 70%. Conversely, the values diverge significantly for the subsequent PCs. Specifically, PC2 ranges between 17% to 20% for VMM and is about 28% for OBM. The remaining PCs show very low values following a trend, whereby the percentage of variation for OBM is roughly half that of VMM (Table 1). Furthermore, the results of the Pearson correlation tests are congruent with these observations, indicating that PC1 is very similar across the three evaluated settings (Table 2). PC2 tends to be more variable, showing a less pronounced relationship, particularly between OBM and VMM (Table 2). The difference between these approaches is exacerbated when analyzing PC3, where no correlation is observed between OBM and VMM. Results of the Mantel tests for both the bidimensional (PC1 and PC2) and the three-dimensional morphospaces (PC1, PC2, and PC3) demonstrate a significant association between the distance matrices of the studied settings, which is also reflected in high correlation values. (Table 3). Therefore, these observations would confirm the similarity of the general structure of the morphospaces obtained. Mantel tests usefulness for spatial analysis has been put in doubt by Legendre et al. (2015). However, given that in this study we are comparing morphospaces formed by principal components, the assumptions required for this test are fulfilled (i.e., linear relationships, and correspondence of values between distance matrices; see Legendre et al., 2015; Appendix 2). In addition, the Mantel test results are further confirmed by the strong significant correlations found between the multidimensional morphospaces using two-block PLS analyses (Table 4).

Considering the transformations encompassed by each PC, the obtained predicted morphologies are similar between the two methods, and they are identical for both cases of VMM (Figure 2, Appendix 2). The transformations along PC1 and PC2 are consistent with previous findings. PC1 remains primarily associated with the degree of compression and, to a lesser extent, with the lateral extension of the imprint zone. PC2 involves a dorsoventral elongation/compression along the axis of symmetry and defines the height of the imprint zone (or in other words, the degree of whorl overlap). However, the most notable distinction lies in how each method represents the imprint zone. In the case of OBM, this region appears as a smooth curve that connects both flanks (Figure 2B). Generally, there is a lack of definition in the umbilical walls, suggesting a limitation derived from the curve generation process. This peculiarity appears to be more prominent in the subsequent principal components, especially for PC3, which apparently determines the overall shape of the umbilical walls (Figure 3, Figure 4, Figure 5). However, it should be noted that the amount of variance represented by PC3 is small, accounting for less than 3% for OBM and for about 6 % for VMM.

Concerning the distribution of the genera within the two-dimensional morphospace (formed by PC1 and PC2), differences can be seen between the relative distribution of some taxa depending on the method employed. Nevertheless, it is evident that certain clusters and some relative positions are consistent between the two approaches (Figure 5). Notably, most of the differences between these clusters might be related to the imprint zone as well. These differences are more evident when PC3 is taken into account (Figure 3, Figure 4, Figure 5). In this sense, for OBM the morphospace formed by PC1 and PC3 shows a general crescent shape, displaying the lowest values around the extreme PC3 scores (Figure 3B). In contrast, the morphospace for both VMM configurations exhibits no distinct shape, and the taxa are distributed relatively evenly (Figure 3A). Furthermore, for both methods, it is also noted that the most densely populated area is situated within the interval PC1 score = [0.1; -0.2]; which is congruent with previous findings documented by Morón-Alfonso et al. (2023).

DISCUSSION

The results of this study align with previous findings concerning the variation in the whorl profile. Specifically, the transformations represented by PC1 and PC2, which are consistent across methods and contribute to the robustness of the variation patterns previously reported (Figure 2; Morón-Alfonso et al., 2023, figure 8). However, an important difference with respect to previous finding lies in the percentage of variance represented by PC1, which reaches up to 70% for the VMM 44-SL setting, and slightly drops to 68% and 66% for VMM 56-SL and OBM, respectively. This value is notably higher compared to results obtained using simpler VMM 18 SL configurations (i.e., around 56% for Morón-Alfonso et al., 2021; and 55% for Morón-Alfonso et al., 2023). The differences observed between the 18 SL and the other conditions can be attributed to the fact that the 18 SL served as an economical, albeit less accurate, biological model for the whorl profile shape compared to the newer settings. However, as with any simplified biological model, it is likely that some observed variation might have been misrepresented or distributed across other principal components (PCs, Gunawardena, 2014). Increasing the number of SL enables the evaluation of additional regions of the whorl profile that were not previously accounted for, thus altering the resulting variation. Furthermore, the percentage of variance attributed to PC1 is derived from subtracting its value from the cumulative variance of the remaining PCs (Table 1). As a result, the transformation represented in PC1 would likely be more significant in defining the whorl profile shape than previously assumed. However, to confirm this statement, a replication test applying these methods (OBM and VMM) to the complete sample of 300 specimens will be necessary.

Concerning the two SL configurations for VMM (44-SL vs 56-SL), we do not find considerable differences between settings, showing only approximately 2% less variance explained by PC1 for 56-SL (Table 1-Table 2). This value also correlates with a slightly higher percentage of variance attributed to PC2 for 56-SL, which is likely associated with the elongation or compression of the imprint zone (degree of whorl overlap) characteristic of PC2. As follows, these observations suggest that reducing the number of semi-landmarks in the imprint zone does not greatly impact the obtained results. Nonetheless, it should be noted that simpler configurations could be more suitable for studies where the quantity of landmarks is pertinent for the calculations, such as cladistic analyses (Catalano et al., 2010; Goloboff and Catalano, 2011; 2016; Catalano and Goloboff, 2018).

Regarding the distinctions among the evaluated methods, the most significant difference lies in how each approach describes the imprint zone. In OBM, this region is rendered as a smooth curve, most likely resulting from the outline transformation process required for Fourier Analysis. This effect may also be explained by the fact that the VMM methods, even the 44 SL configuration, have a dense sampling of landmarks around the imprint zone, while the Fourier method describes smaller details as additional harmonics. Consequently, the transformations linked to the umbilical wall are primarily represented in PC3, producing a segregation of taxa with either a smooth or pronounced imprint zone, showing two distinct groups. The observed differentiation contributes to the resultant crescent-shaped distribution in the bidimensional morphospace (Figure 3B, Appendix 2). Conversely, the transformations associated with PC3 for VMM are also related to the shape of the imprint zone, but they are more specifically linked to the lateral dimensions of the umbilical walls (Figure 3A). Hence, the resulting three-dimensional morphospace lacks a distinctive shape, with specimens being distributed relatively evenly (Appendix 2). In Morón-Alfonso et al. (2023), it was observed that some of the less significant principal components (i.e., PC3 onwards) might be important in defining certain internal clades of ammonoids. Therefore, if PC3 is indeed affected by a limitation within the OBM approach, it is plausible that specific groups might not be precisely identified in more extensive analyses.

With respect to the application of the methods, as it is presented in this work, employing virtual models proves to be useful for generating the data required for each analysis. In general, OBM stands out as a faster and more practical approach, because the virtual shapes created by the program can be directly rendered into silhouettes utilized by the functions of the R package Momocs (Bonhomme et al., 2014). On the contrary, VMM is a labor-intensive method, requiring the extraction of vertices from the virtual models. VMM typically involves an intermediate step in which the coordinates of the boundary semi-landmarks are extracted using a function that is adjusted to the evaluated configuration, which implies that implementing this method is comparatively more challenging. However, the resulting predicted morphologies and the relative distance between points appear to be more accurate. Based on these observations, OBM might be optimal for cases where the taxa under evaluation have a limited imprint zone (i.e., evolute morphologies) or a smooth umbilical wall (e.g., such as Pictetia or Crioceratites, Hoffmann et al., 2009; Bert et al., 2021), and in cases dealing with large datasets, which would be too time-consuming to assess with VMM. On the other hand, VMM would be better suited for cases where this region is well-defined, with either stepped umbilical walls or acute angles in the imprint zone (e.g., Acutimitoceras, Pachydiscus, Macellari, 1986; Ebbighausen and Bockwinkel, 2007).

CONCLUSIONS

The transformations depicted by PC1 and PC2 seem consistent across methods and are congruent with previously reported variation patterns. For VMM the variation summarized by these principal components are 87% for 44-SL and 88% for 56-SL. For OBM the variation resumed by these two components is about 94%. Compared to previous findings employing simpler 18 semi-landmark configurations for VMM, where PC1 accounted for 55%, here we show that PC1 accounts for up to 70% of the variation with a 44 semi-landmarks configuration and 68% with a 56 semi-landmark configuration. Reducing the number of semi-landmarks representing the imprint zone in VMM does not significantly impact the obtained results. The variation in the imprint zone does not appear to be the most crucial aspect of shape variation, as it is predominantly reflected in PC2 or PC3. Therefore, it seems that at this intergeneric scale, the primary signal (PC1) is related to more or less dorso-ventrally elongated whorl profiles. Differences between methods (VMM vs OBM) lies principally in their interpretation of the imprint zone and the transformations linked to this region, primarily reflected by PC3. Overall, VMM exhibits a finer quantification of the imprint zone compared to OBM and would be suitable for taxa exhibiting highly defined umbilical walls. Conversely, OBM would be preferable for taxa with smooth umbilical walls or with a reduced imprint zone (evolute taxa).

ACKNOWLEDGMENTS

Thanks to M.C. Rodríguez Amenábar (Instituto Antártico Argentino, Buenos Aires, Argentina) and M. Tanuz (Universidad de Buenos Aires, Buenos Aires, Argentina) for the loan of specimens under their care. Thanks to the Ruhr Universität for providing some of the tomographic datasets used in this work. Special thanks to the cephalopod research community, the online repositories, and to all the authors that provided free open-access to the data required for this study. Lastly, thanks to the suggestions of the anonymous reviewers, which greatly improve the quality of this manuscript. Founding for this project was provided by PICT 2021 4899 (to DMA). This is the contribution R-480 of the Instituto de Estudios Andinos ‘Don Pablo Groeber’ (IDEAN, UBA-CONICET).

REFERENCES

Adams, D.C., Rohlf, F.J., and Slice, D.E. 2004. Geometric morphometrics: Ten years of progress following the ‘revolution’. Italian Journal of Zoology, 71:5-16.
https://doi.org/10.1080/11250000409356545

Adams, D.C., Rohlf, F., and Slice, D. 2013. A field comes of age: Geometric morphometrics in the 21st century. Hystrix, 24:7-14.
https://doi.org/10.4404/hystrix-24.1-6283

Adams, D.C., Collyer, M., Kaliontzopoulou, A., and Baken, E.K. 2021. Geomorph: Software for geometric morphometric analyses. R package version 4.0. Methods in Ecology and Evolution, 4:393-399.

Allaire, N., Ginot, S., De Baets, K., Korn, D., Goudemand, N., Monnet, C., and Cronier, C. 2023. Morphological disparity of early ammonoids: A geometric morphometric approach to investigate conch geometry. Acta Palaeontologica Polonica, 68:193-212.
https://doi.org/10.4202/app.01033.2022

Allen, E.G. 2007. Understanding ammonoid sutures: New insight into the dynamic evolution of paleozoic suture morphology, p. 159-180. In Landman, N.H., Davis, R.A. and Mapes, R.H. (eds.), Cephalopods Present and Past: New Insights and Fresh Perspectives. Springer Netherlands, Dordrecht.
https://doi.org/10.1007/978-1-4020-6806-5_8

Baken, E.K., Collyer, M.L., Kaliontzopoulou, A., and Adams, D.C. 2021. Geomorph v4.0 and gmShiny: Enhanced analytics and a new graphical interface for a comprehensive morphometric experience. Methods in Ecology and Evolution, 12:2355-2363.
https://doi.org/10.1111/2041-210X.13723

Bert, D., Reboulet, S., Vernet, B., Bersac, S., and Canut, L. 2021. Early Crioceratites (heteromorphic ammonites) from the lower Hauterivian of south-eastern France: systematics, intraspecific variation and biostratigraphic implications. Cretaceous Research, 126:104903.
https://doi.org/10.1016/j.cretres.2021.104903

Bischof, E.A. and Lehmann, J. 2020. Ontogenetic analysis of Anisian (Middle Triassic) Ptychitid ammonoids from Nevada, USA. Journal of Paleontology, 94:829-851.
https://doi.org/10.1017/jpa.2020.25

Bischof, E.A., Schlüter, N., Korn, D., and Lehmann, J. 2021. Ontogeny of highly variable ceratitid ammonoids from the Anisian (Middle Triassic). PeerJ, 9e10931:1-26.
https://doi.org/10.7717/peerj.10931

Blender Online Community 2022. Blender, a 3D Modelling and Rendering Package. https://www.blender.org/download/releases/2-81/

Bonhomme, V., Picq, S., Gaucherel, C., and Claude, J. 2014. Momocs: Outline Analysis Using R. Journal of Statistical Software, 56:1-24.
https://doi.org/10.18637/jss.v056.i13

Catalano, S.A., Goloboff, P.A., and Giannini, N.P. 2010. Phylogenetic morphometrics (I): the use of landmark data in a phylogenetic framework. Cladistics, 26:539-549.
https://doi.org/10.1111/j.1096-0031.2010.00302.x

Catalano, S.A. and Goloboff, P.A. 2018. A guide for the analysis of continuous and landmark characters in TNT (Tree Analysis using New Technologies). Technical Report, 1.
https://doi.org/10.13140/RG.2.2.23797.27360

Collyer, M.L. and Adams, D.C. 2018. RRPP: An r package for fitting linear models to high-dimensional data using residual randomization. British Ecological Society, 9:1772-1779.
https://doi.org/10.1111/2041-210X.13029

Collyer, M. and Adams, D.C. 2023. RRPP: Linear Model Evaluation with Randomized Residuals in a Permutation Procedure.
https://CRAN.R-project.org/package=RRPP

Courville, P. and Crônier, C. 2016. Diversity or disparity in the Jurassic (Upper Callovian) genus Kosmoceras (Ammonitina): A morphometric approach. Journal of Paleontology, 79:944-953. https://doi.org/10.1666/0022-3360(2005)079[0944:DODITJ]2.0.CO;2

Dommergues, J.-L., Laurin, B., and Meister, C. 1996. Evolution of Ammonoid Morphospace During the Early Jurassic Radiation. Paleobiology, 22:219-240.

Ebbighausen, V. and Bockwinkel, J. 2007. Tournaisian (Early Carboniferous/Mississippian) ammonoids from the Ma'der Basin (Anti-Atlas, Morocco). Fossil Record, 10:125-163.
https://doi.org/10.1002/mmng.200700003

Ebbighausen, V. and Korn, D. 2007. Conch geometry and ontogenetic trajectories in the triangularly coiled Late Devonian ammonoid Wocklumeria and related genera. Neues Jahrbuch für Geologie und Paläontologie - Abhandlungen, 244:9-41.
https://doi.org/10.1127/0077-7749/2007/0244-0009

Erlich, A., Moulton, D.E., Goriely, A., and Chirat, R. 2016. Morphomechanics and developmental constraints in the evolution of ammonites shell form. Journal of Experimental Zoology Part B: Molecular and Developmental Evolution, 326:437-450.
https://doi.org/10.1002/jez.b.22716

Gilli, M., Maringer, D., and Schumann, E. 2019. Chapter 6 - Generating random numbers, p. 103-132. In Gilli, M., Maringer, D., and Schumann, E. (eds.), Numerical Methods and Optimization in Finance (Second Edition). Academic Press.
https://doi.org/10.1016/B978-0-12-815065-8.00017-0

Goloboff, P.A. and Catalano, S. 2011. Phylogenetic morphometrics (II): Algorithms for landmark optimization. Cladistics, 27:42-51.
https://doi.org/10.1111/j.1096-0031.2010.00318.x

Goloboff, P.A. and Catalano, S.A. 2016. TNT version 1.5, including a full implementation of phylogenetic morphometrics. Cladistics, 32:221-238.
https://doi.org/10.1111/cla.12160

Gunawardena, J. 2014. Models in biology: ‘accurate descriptions of our pathetic thinking’. BMC Biology, 12:29.
https://doi.org/10.1186/1741-7007-12-29

Hoffmann, R., Keupp, H., and Wiese, F. 2009. The systematic position of the Lower Cretaceous heteromorphic ammonite Pictetia Uhlig, 1883. Paläontologische Zeitschrift, 83:521-531.
https://doi.org/10.1007/s12542-009-0036-2

Kant, R. 1973. Allometrisches Wachstum paläozoischer Ammonoideen: Variabilität und Korrelation einiger Merkmale. Neues Jahrbuch für Geologie und Paläontologie - Abhandlungen, 143:153-192.

Klein, C. and Korn, D. 2014. A morphometric approach to conch ontogeny of Cymaclymenia and related genera (Ammonoidea, Late Devonian). Fossil Record, 17:1-32. 10.5194/fr-17-1-2014

Klug, C., Kröger, B., Vinther, J., Fuchs, D., and De Baets, K. 2015a. Ancestry, Origin and Early Evolution of Ammonoids, p. 3-24. In Klug, C., Korn, D., De Baets, K., Kruta, I., and Mapes, R.H. (eds.), Ammonoid Paleobiology: From macroevolution to paleogeography. Springer Netherlands, Dordrecht.
https://doi.org/10.1007/978-94-017-9633-0_1

Klug, C., Korn, D., Landman, N.H., Tanabe, K., De Baets, K., and Naglik, C. 2015b. Describing Ammonoid Conchs, p. 3-24. In Klug, C., Korn, D., De Baets, K., Kruta, I., and Mapes, R.H. (eds.), Ammonoid Paleobiology: From anatomy to ecology. Topics in Geobiology, vol 43. Springer Netherlands, Dordrecht.
https://doi.org/10.1007/978-94-017-9630-9_1

Korn, D. 2010. A key for the description of Palaeozoic ammonoids. Fossil Record, 13:5-12. https://doi.org/10.1002/mmng.200900008

Korn, D. 2012. Quantification of ontogenetic allometry in ammonoids. Evolution & Development, 14:501-514.
https://doi.org/10.1111/ede.12003

Korn, D. and Klug, C. 2012. Palaeozoic ammonoids - diversity and development of conch morphology, p. 491-534. In Talent, J.A. (ed.), Earth and Life: Global Biodiversity, Extinction Intervals and Biogeographic Perturbations Through Time. Springer Netherlands, Dordrecht.
https://doi.org/10.1007/978-90-481-3428-1_15

Kullmann, J. and Scheuch, J. 1970. Wachstums-änderungen in der onto-genese paläozoischer ammonoideen. Lethaia, 3:397-412.
https://doi.org/10.1111/j.1502-3931.1970.tb00831.x

Landman, N.H., Garb, M.P., Rovelli, R., Ebel, D.S., and Edwards, L.E. 2012. Short-Term Survival of Ammonites in New Jersey After the End-Cretaceous Bolide Impact. Acta Palaeontologica Polonica, 57:703-715.
https://doi.org/10.4202/app.2011.0068

Legendre, P., Fortin, M.-J., and Borcard, D. 2015. Should the Mantel test be used in spatial analysis? Methods in Ecology and Evolution, 6:1239-1247.
https://doi.org/10.1111/2041-210X.12425

Macellari, C. 1986. Late Campanian-Maastrichtian Ammonite Fauna from Seymour Island (Antarctic Peninsula). Journal of Paleontology, 60:1-55.
https://doi.org/10.1017/S0022336000060765

Machalski, M. and Heinberg, C. 2005. Evidence for ammonite survival into the Danian (Paleogene) from the Cerithium Limestone at Stevns Klint, Denmark. Bulletin of the Geological Society of Denmark, 52:1-12.
https://doi.org/10.37570/bgsd-2005-52-08

Milla Carmona, P. 2022. Morphospace 0.0.0. R package version 4.2.1. CRAN.R virtual repository.
https://github.com/millacarmona/morphospace.git

Mitteroecker, P. and Schaefer, K. 2022. Thirty years of geometric morphometrics: Achievements, challenges, and the ongoing quest for biological meaningfulness. American Journal of Biological Anthropology, 178:181-210.
https://doi.org/10.1002/ajpa.24531

Monnet, C., Brayard, A., and Brosse, M. 2015. Evolutionary trends of Triassic ammonoids, p. 25-50. In Klug, C., Korn, D., De Baets, K., Kruta, I., and Mapes, R.H. (eds.), Ammonoid Paleobiology: From macroevolution to paleogeography. Topics in Geobiology, vol 43. Springer Netherlands, Dordrecht.
https://doi.org/10.1007/978-94-017-9633-0_2

Morón-Alfonso, D., Hoffmann, R., and Cichowolski, M. 2021. Geometric morphometrics in ammonoids based on virtual modelling. Palaeontologia Electronica, 24.3.a29.
https://doi.org/10.26879/1157

Morón-Alfonso, D., Cichowolski, M., Hoffmann, R., Korn, D., Vennari, V., and Allaire, N. 2023. The intriguing shapes of the ammonoid whorl. Palaeontologia Electronica, 26:1-23.
https://doi.org/10.26879/1263

Neige, P. 1999. The Use of Landmarks to Describe Ammonite Shape, p. 263-272. In Olóriz, F. and Rodríguez-Tovar, F.J. (eds.), Advancing Research on Living and Fossil Cephalopods. Springer US, Boston, MA.
https://doi.org/10.1007/978-1-4615-4837-9_20

Olsen, A.M. 2017. Feeding ecology is the primary driver of beak shape diversification in waterfowl. Functional Ecology, 31:1985-1995.
https://doi.org/10.1111/1365-2435.12890

Saunders, W.B. and Swan, A.R.H. 1984. Morphology and Morphologic Diversity of Mid-Carboniferous (Namurian) Ammonoids in Time and Space. Paleobiology, 10:195-28.
https://www.jstor.org/stable/2400397

Saunders, W.B., Work, D.M., and Svetlana, V.N. 2004. The Evolutionary History of Shell Geometry in Paleozoic Ammonoids. Paleobiology, 30:19-43.

Schlager, S. 2020. Morpho and Rvcg -- Shape Analysis in R, p. 217-256. In Guoyan, Z., Shuo, L., and Gabor, S. (eds.), Statistical Shape and Deformation Analysis. Academic Press.
https://doi.org/10.1016/B978-0-12-810493-4.00011-0

Tajika, A. and Klug, C. 2020. How many ontogenetic points are needed to accurately describe the ontogeny of a cephalopod conch? A case study of the modern nautilid Nautilus pompilius. PeerJ, 8:e8849:1-14.
https://doi.org/10.7717/peerj.8849

Wegerer, M., De Baets, K., and Korn, D. 2018. Quantitative analysis of suture lines in Carboniferous ammonoids. Fossil Record, 21:223-236.
https://doi.org/10.5194/fr-21-223-2018