GM in ammonoids virtual models

Geometric morphometrics in ammonoids based on virtual modelling

Daniel A. Morón-Alfonso, René Hoffmann, and Marcela Cichowolski

Article number: 24.3.a29
https://doi.org/10.26879/1157
Copyright Paleontological Society, September 2021

Author biographies
Plain-language and multi-lingual abstracts
PDF version

Submission: 24 March 2021. Acceptance: 6 September 2021.

ABSTRACT

Linear morphometrics is the most widely applied technique to study the variation of the conch morphology in ammonoids and other ectocochleate cephalopods. However, because this method frequently relies upon a few linear measurements, it lacks the explanatory power to accurately characterize the shape of the whorl cross-section, which is instead discussed solely in descriptive terms, e.g., elliptical, triangular, or subquadrate. Here, we introduce a landmark-based geometric morphometric approach to study ammonoid whorl cross-sections, derived from the regularly used morphometric parameters in cephalopods. This new technique uses virtual modelling to generate semilandmark configurations and virtual models of whorl cross-sections. We applied it to study 50 ammonoid specimens belonging to 48 genera exhibiting a wide range of morphologies and ages. Results indicate that this new method is appropriate to describe the shape of ammonoid whorl cross-sections, allowing us to construct a morphospace showing several biological patterns (e.g., clustering and homeomorphy), and complex morphological transformations that, in some cases, correlate with evolutionary tendencies described by previous authors. Further, this technique can be used to generate the basic segment required for the elaboration of the virtual models employed in hydrostatic and hydrodynamic studies.

Daniel A. Morón-Alfonso. Universidad de Buenos Aires, Facultad de Ciencias Exactas y Naturales, Departamento de Ciencias Geológicas, Área de Paleontología, Ciudad Universitaria, Pab. 2, C1428EGA, Buenos Aires, Argentina. CONICET-Universidad de Buenos Aires, Instituto de Estudios Andinos “Don Pablo Groeber” (IDEAN), Buenos Aires, Argentina. paleokarzis@gmail.com
René Hoffmann. Institute of Geology, Mineralogy, & Geophysics, Ruhr-Universität Bochum, 44801 Bochum, Germany. Rene.Hoffmann@rub.de
Marcela Cichowolski. Universidad de Buenos Aires, Facultad de Ciencias Exactas y Naturales, Departamento de Ciencias Geológicas, Área de Paleontología, Ciudad Universitaria, Pab. 2, C1428EGA, Buenos Aires, Argentina. CONICET-Universidad de Buenos Aires, Instituto de Estudios Andinos “Don Pablo Groeber” (IDEAN), Buenos Aires, Argentina. mcicho@gl.fcen.uba.ar

Keywords: Cephalopoda; Ammonoidea; geometric morphometric; conch; whorl

Final citation: Morón-Alfonso, Daniel A., Hoffmann, René, and Cichowolski, Marcela. 2021. Geometric morphometrics in ammonoids based on virtual modelling. Palaeontologia Electronica, 24(3):a29. https://doi.org/10.26879/1157
palaeo-electronica.org/content/2021/3449-gm-in-ammonoids-virtual-models

Copyright: September 2021 Paleontological Society.
This is an open access article distributed under the terms of Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0), which permits users to copy and redistribute the material in any medium or format, provided it is not used for commercial purposes and the original author and source are credited, with indications if any changes are made.
creativecommons.org/licenses/by-nc-sa/4.0/

INTRODUCTION

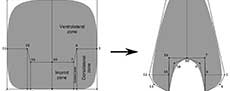
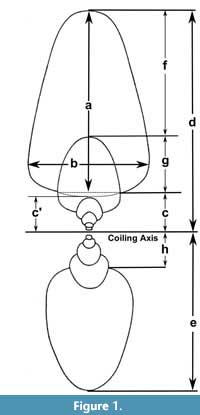The study of biological variation is based on the comparison of features (e.g., composition, structure) of one or more organisms using distinct methodologies (e.g., spectrometry, morphometry) to characterize it (Adams et al., 2004). In some cases, this variation is expressed in the morphology of different components, showing modifications in development within a species (e.g., sexual dimorphism) or through the evolutionary history of a group (Claude, 2008). In ectocochlate cephalopods, the need to increase the descriptive power to study the morphological variation of the conch has prompted the development of several morphometrical models (Table 1). In general, these methods employ linear measurements as quantitative descriptions of the conch morphology combined with statistical analyses to find biological patterns (e.g., ecological constraints, and evolutionary tendencies, Adams et al., 2004). Early attempts to assess the conch morphological variation used simple linear measurements of the conch collected from cross or longitudinal sections (Moseley, 1838; Sandberger, 1851, 1853, 1857; Trueman, 1940). More recently, Raup (1967) and Raup and Michelson (1965) refined this technique, focusing on the study of the ammonoid conch geometry and adapting the Raupian model, previously defined for gastropods (Raup, 1961, 1966; Urdy et al., 2010). The Raupian model consists of four geometric parameters (S: the shape of the generating curve, W: the whorl expansion rate, D: the position of the generating curve relative to the coiling axis, and T: the rate of whorl translation), calculated from five linear measurements (Figure 1). Korn (1997, 2010) adopted most of these linear measurements, incorporating derived parameters, indices, and rates (e.g., the imprint zone rate), centering on the evaluation of the ontogenetic trajectories in Palaeozoic ammonoids (Figure 1). Later, this modified version of the Raupian model was proposed as the ‘standard’ to characterize the conch morphology for all (Devonian to Cretaceous) ammonoids (Klug et al., 2015). During the last decade, several morphometric models were proposed to study the conch morphology and morphogenesis, showing an increasing degree of complexity as more factors were considered. These models have been successfully applied to explain the origin of distinct ribbing patterns and their relationship with other parameters (e.g., Erlich et al., 2016, Table 1) to test the paleoecology of ectocochleate cephalopods (for a review see Naglik et al., 2015) or to define ecomorphospaces (e.g., Westermann, 1996, 2013; Ritterbush, 2015; Tendler et al., 2015). Recently, these methods have been integrated to machine learning testing the potential for future automated ammonoid taxonomic assignment (Foxon, 2021).

Although morphometric models are widely accepted as a suitable tool to study ectocochleate cephalopods, Gerber (2017) noted that these methods possess underlying constraints that can hinder the complete description of the conch morphological variation, suggesting that the landmark-based framework (geometric morphometric, GM) could be more suitable. For example, the complex shape of the whorl cross-section cannot be accurately characterized by simple linear measurements, and it is usually typified by descriptive terms that cannot be statistically compared between samples (Figure 1, Smith, 1986). Previous applications of GM methods in ectocochleate cephalopods include the evaluation of the suture line and conch morphology in ammonoids using outline-based methods (Korn and Klug, 2012; Klein and Korn, 2014; Allen, 2016; Wegerer et al., 2018), and landmark-based methods to analyze the morphologic variation on specific ammonoid taxa (Neige, 1999; Courville and Crônier, 2016; Bischof et al., 2021). Results of these studies showed the potential of GM methods to study the biologic variation in ectocochleate cephalopods. In this work, we introduce an alternative technique to study the shape of whorl cross-sections using semilandmarks, derived from the virtual modelling methodology described in a previous study (Morón-Alfonso et al., 2020). We use the term “semilandmarks” instead of “landmarks”, given that the homology between these points cannot be determined precisely from the curves that define the whorl shape of ammonoids. As follows, we apply this method to study the whorl cross-section of 50 ammonoid specimens representing 49 species, defining their semilandmark configurations and generating the corresponding virtual models.

MATERIALS AND METHODS

The use of virtual modelling has improved our understanding of the hydrodynamic and hydrostatic properties of ectochocleate cephalopod shells (e.g., Peterman et al., 2019a, 2019b, 2020; Hebdon et al., 2020). First described by Peterman et al. (2019a), this method consists of the iteration of a virtual whorl cross-section following a pathway in a three-dimensional space, allowing it to generate a virtual model of the cephalopod conch for experimentation. Based on this approach, Morón-Alfonso et al. (2020) described a modelling process to construct complex planispiral ammonoid conchs noting that one of the advantages of the method was the flexibility to model non-elliptical whorl cross-sections. We go one step further, standardizing this modelling technique to study the shape of the whorl cross-section implementing a geometric morphometric approach.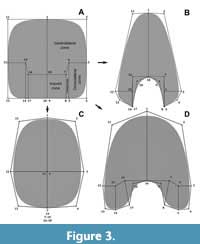 This new method consists of the modification of a simple plane using the subdivision surface modifier included in the open-source program Blender 2.92 (Blender Online Community, 2021) based on the Catmull and Clark (1978) algorithm (Figure 2). Subdivision surface is a widespread procedure used in computer graphics to generate complex three-dimensional shapes from simple geometries. This algorithm increases exponentially the number of vertices, edges, and faces of a mesh through simple rules (see Catmull and Clark, 1978; Sabin, 2002). Every time the algorithm is applied, the surfaces of polygonal geometries become smoother at the cost of a smaller size (Figure 2). This process can be modified by increasing the number of edges (and hence the number of vertices) to model more complex two- and three-dimensional shapes (Sabin, 2002). Despite that there are infinite ways to model whorl cross-sections of cephalopod conchs using this technique, based upon the standard dimensional linear measurements used in ammonoids (Figure 1), we can divide the whorl cross-section of a theoretical specimen into six curves and four regions defined by 18 vertices/semilandmarks (Figure 3). The distance between these vertices can be extrapolated to the standard parameters used for the cephalopod conchs (Figure 3). This basic configuration can be modified including more features (e.g., ornamentation) to obtain more detailed models. In some evolute ammonoids, the imprint and contact zones are nonexistent or reduced. In this special case, certain semilandmarks can share the same coordinates (i.e., merging the vertices; Figure 3).

This configuration can also be used to model the whorl cross-section of other ectocochleate cephalopods such as heteromorph ammonoids and nautiloids (Figure 3), or be applied to the conchs of endocochleates like modern Spirula and, potentially, to other organisms with spirally coiled hard parts like gastropods or foraminifera. A key advantage of this new technique to define semilandmarks with respect to other GM methods is the capacity to directly translate the semilandmark configurations to complex virtual models using the modelling program. Consequently, any theoretical or transformed semilandmark configuration (e.g., descaled) can be rendered to a virtual model for comparison. Hereafter, we will refer to this operation as ‘reverse modelling’.

Data

Once the basic theoretical model and the number of semilandmarks are determined, images of real ammonoid cross-sections can be used as stencils exporting them as empties in the Blender 2.91 workspace. To test the reliability and constraints of the method, we used images of 50 ammonoid specimens to construct a basic morphospace and study the patterns obtained from it. The images consisted of orthoslices collected from physical-optical, medical, and micro-CT data, coupled with photographs and illustrations of the specimens with a proper orientation found in repositories and the literature. The number of species is relatively low (due to a lack of available conch cross-sections), and represents 49 species belonging to 48 genera ranging from the Late Devonian to Late Cretaceous, showing a wide spectrum of morphologies and stratigraphic age ranges (Table 2). The repository information, landmark configurations, and more detailed data of the specimens can be found in Appendix 1, and for a video tutorial of the virtual modelling method applied to these samples see Appendix 2. For partially eroded specimens only the best-preserved flank was modelled and then mirrored to obtain a complete virtual model of the whorl cross-section (hereafter designated as virtual whorl cross-section). For this work, we performed four levels of subdivisions as the standard to generate the virtual models.

Statistical Analyses

The data including the semilandmark coordinates were exported from the modelling software to a spreadsheet using PAST 4.06 (Hammer et al., 2001). These data were then processed to generate a Clarion TopScan (TPS) file required for the analysis. Additional data containing the ID of the specimens, the maximum diameter, and the mean stratigraphic age range (calculated as an average between the maximum age and minimum age of the taxon) were included in a table separately. Following, this data was loaded to an R 4.04 environment and a Generalized Procrustes Analysis (GPA) and statistical analysis were performed using the Morpho and Geomorph Packages (Adams and Otarola-Castillo, 2013; Schlager, 2017). The GPA translates all the semilandmark configurations to the origin, scales them to unit-centroid size, and optimally rotates them (using a least-squares criterion) until the coordinates of corresponding points align as closely as possible. The resulting aligned Procrustes coordinates represent the shape of each specimen and are found in a curved space related to Kendall's shape space (Kendall, 1984). The multivariate analysis consisted of a Principal Component Analysis (PCA) and a Multivariate Linear Regression (MLR). PCA is used for reducing the dimensionality of complex datasets, increasing interpretability, and generating predictive models, but at the same time minimizing information loss (Jolliffe and Cadima, 2016). The MLR was performed using one independent variate (the mean stratigraphic age range or the diameter) and n dependent variates (Principal Components). This analysis fits each dependent variate separately to the independent variate using simple linear regressions. Further, an overall Multivariate Analysis of Variance (MANOVA) test of the multivariate regression significance is provided. The data obtained from the PCA such as the predictive semilandmark configurations were submitted to the reverse modelling to generate the matching virtual whorl cross-section for each specimen.

Evaluation of Morphometric Patterns

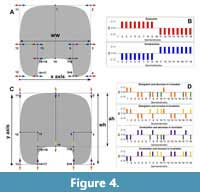There have been described several patterns of covariation in ammonoids related to the morphology of the whorl cross-section (De Baets et al., 2015; Monnet et al., 2015b, 2015c). Therefore, a valuable comparison is testing if these patterns, described from morphometric analyses, are observed using GM methods as well. This evaluation can be done approximating a theoretical whorl-section to the standard model and applying transformations related to the variation of the whorl cross-section; in this case, the aperture height (ah), the whorl width (ww), and the whorl height (wh, Figure 4). The variation of the whorl width will be associated with scaling in the x-axis implying an expansion or compression in the horizontal plane (Figure 4A-B), and the variation of the aperture height and whorl height are linked to translations in the y-axis (Figure 4C-D). The whorl height is recognized as an elongation or contraction, while the aperture height is associated with changes in the size of the imprint zone. Both vary depending on the degree of involution (Figure 4C-D). Comparison between covariation patterns can be difficult to assess solely from the transformation vectors. Therefore, we used simple graph bars to illustrate the change in position (translation) in each semilandmark (Figure 4). As follows, the total variation will be a combination of the x and y vectorial components.

Special Cases

To complement the discussion and to portray some of the possible applications of the methodology, an examination of two special cases was incorporated in the study. The first case consists of the inclusion of two Maorites species in the statistical analyses, M. seymourianus (Kilian and Reboul, 1909) and M. densicostatus (Kilian and Reboul, 1909), both from the López de Bertodano Formation (Campanian-Maastrichtian) of the James Ross Basin, Antarctica. These species have a well-established stratigraphical framework (Tobin et al., 2012; Witts et al., 2016), and previous research of their ontogenetic trajectories showed a possible case of speciation involving paedomorphism (Morón-Alfonso, 2019), likely registered in the fossil record due to the unusually high average sedimentation rate determined for this formation (0.1 to 0.2 mm per year, Witts et al., 2016; Scasso et al., 2020). Evaluation of the variation of the whorl cross-section between these species elucidated the processes implicated during an evolutionary turnover.

The second special case involved the elaboration of a complementary PCA and PGA including additional whorl cross-sections at different diameters of an exceptionally well-preserved Proleymeriella schrammeni (Jacob, 1907) specimen used in a previous study (Hoffmann et al., 2021). The resulting transformations between the PC-scores were used to analyze the change of the whorl cross-section through ontogeny. For this case, despite that the whorl cross-section does not define the general geometry of the conch at a given diameter it could indicate the transition between different ontogenetic stages, signalling periods in which the morphology of the whorl cross-section is similar among different taxa (e.g., morphologic phylotypic periods; Levin et al., 2016).

RESULTS

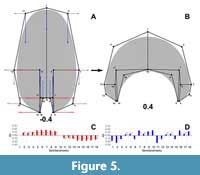The variation for the virtual whorl cross-sections is explained by 29 principal components (PCs, Appendix 3). The first three PCs explain around 90% of the variation found in the sample (Table 3). Further, predicted semilandmark configurations were calculated for each of these PCs and the reverse modelling method was applied to illustrate the principal transformations (Figure 5, Figure 6, Figure 7). Going from negative to positive values, the transformations in PC1 (when compared to the expected patterns of variation) are consistent with an expansion and contraction of the whorl cross-section, showing an increase of the involution degree (Figure 5). 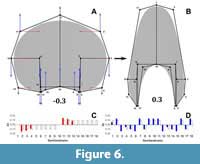The semilandmarks that display the highest variation are related to the imprint zone (Figure 5). In contrast, the transformation in PC2 adjusts to a compression of the whorl cross-section localized in the peripheric semilandmarks, and an overall elongation alongside an increase in the involution degree (Figure 6). Accordingly, PC2 determines the general outline of the whorl cross-section going from ellipsoidal to lanceolate shapes. 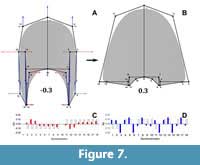Following, the transformations in PC3 do not adjust completely to any of the expected covariation patterns (Figure 7), and most of the variation is observed on semilandmarks 3, 6, 12, and 15, which are related to the location of the whorl width parameter with respect to the horizontal axis. Consequently, PC3 encompasses changes between rectangular to sub-triangular shapes. When plotted together, these PCs result in a complex three-dimensional morphospace. To ease the interpretations, PC1 was plotted against PC2 and PC3 separately (Figure 8, Figure 9). From this three-dimensional morphospace, homeomorphy and clustering can be distinguished (e.g., Figure 8, Figure 9, between species 29, 31, and among species 26, 37, and 47). To evaluate other biological patterns the PCs were plotted against the maximum diameter and the mean stratigraphic age range (Figure 10). The results are compatible with previous patterns found in ammonoids (i.e., the reduction of the involution through phylogeny as size increased through time). To this effect, and following the polarity of the transformations used in this work, PC1 shows an inverse relationship with the diameter and a direct relationship with the mean stratigraphic age range, showing compression and a decrease in involution as size increases, and the opposite morphologic pattern going from older to younger taxa (Figure 10A-B). Contrary, PC2 shows no significant relationship with the diameter and a weak relationship with the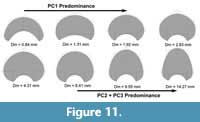 mean stratigraphic age range (Figure 10C-D). MANOVA results for the MLR show the same pattern for the diameter and mean stratigraphic age range showing no significant relationship with the diameter and a weak but significant relationship with the mean stratigraphic age range (Table 4). Finally, we analyzed the ontogenetic changes of P. schrammeni compared to the morphospace obtained from the first PCA. Results are coherent with the transformations obtained for the initial analyses, indicating a predominance of PC1 during early ontogeny (juvenile phase), and PC2 and PC3 reaching adulthood (Figure 11).

DISCUSSION

Virtual Modelling Technique

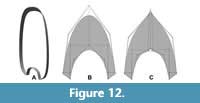The results demonstrate that the semilandmark-based method using virtual modelling is a viable option to study the biological variation of the whorl shape in ammonoids. Moreover, the virtual modelling technique can be combined with the methodology explained in Morón-Alfonso et al. (2020) to generate basic segments required for virtual models employed in hydrodynamic and hydrostatic studies (Figure 12). The modelling of complex whorl shapes with special ornamentation, such as furrows, keels or spines, remain difficult. Their topology could be adjusted in a simplified version of the original whorl cross-section, and the ornamentation can be described separately as a particular feature of the studied sample (Figure 12B). The alternative option is to add more semilandmarks (Figure 12C), which could be important to study the variation in specific taxa. The second constraint is related to the lack of interplay between the modelling platform and the statistical programs used in geometric morphometrics. On this subject, the modelling method can be done quickly, but exporting the data (i.e., the semilandmark coordinates) must be done manually to keep the same arrangement on each sample. Finally, there have been several sophisticated models for studying the ammonoid conch, but models based on linear measurements are still predominant in the field because of their practicality and simplicity (e.g., Tajika and Klug, 2020). Therefore, we note that the virtual modelling technique described here is not designed to replace these morphometric models...actually, the results obtained from both methodologies could be used to evaluate the allometric variation in the specimens (e.g., in this work we evaluate the morphologies against the diameter) or be incorporated to other semilandmark-based methodologies for more complete descriptions (e.g., Gerber, 2017).

Biological Patterns

With our dataset, we were able to elaborate a morphospace showing several possible biological patterns (Figure 9, Figure 10). The transformations in PC1 seem to be related to a covariation pattern, originally obtained from the standard Raupian model, involving an increase in the compression and changes in the involution degree through time. This macroevolutionary tendency may be asserted by increasing the number of species spanning a longer period of time (for a review see Monnet et al., 2015b). However, PC1 only explains around 57% of the variation, which indicates that there is still a considerable range of variation that has not been covered (Table 3). On this subject PC2 (21%) and PC3 (11%) seem to be strongly linked to another pattern rarely assessed quantitatively denominated as the First Buckman’s Rule of Covariation (De Baets et al., 2015; Monnet et al., 2015c). This rule involves a relationship between the degree of involution, compression, and an unaccentuated ornamentation, and it is observed in both the intra- and inter-specific variation of closely related taxa (Monnet et al., 2015c). A relevant case is observed in the Maorites species, M. densicostatus and M. seymourianus. These species share a very similar discoidal and subinvolute conch morphology (following Klug et al., 2015 terminology), and discrimination between both is based on the ornamentation and differences in the whorl width and whorl height in adults (see Morón-Alfonso, 2019). In the morphospace, these species share similar PC-scores for PC1, and most of the variation is explained by PC2 and PC3. An evolutionary tendency towards the more compressed form M. densicostatus was suggested in previous studies, but besides the increase in compression, no other evidence suggested an explanation to this speciation case (Macellari, 1986; Morón-Alfonso, 2019). Because PC2 and PC3 are related to the degree of compression and the shape of the ventral region, these PCs define the general outline of the conch and are likely important to determine its hydrodynamic performance. Further, if this last statement is confirmed using hydrodynamic analyses in complete virtual models of the conch of these species, it could explain the cases of homeomorphy and clustering observed in the morphospace (e.g., Figure 9, specimens 29 and 31), implying a convergent evolution to a potential optimal ecomorphology related to their size.

Regarding the variation of the whorl cross-section in the ontogeny of P. schrammeni, this specimen shows a complex morphological change between whorls. In the present case, PC1 seems to dictate the transformations early in the ontogeny, showing a decrease in the involution degree and expanding the area of the whorl (Figure 11). Contrary, PC2 and PC3 transformations are dominant reaching adulthood, involving a change from a sub-elliptical to a sub-triangular shape. The first observation suggests that PC1 transformations may be related to a process consistent with an increase in inhabitable area, maybe related to a more active lifestyle (creating the space necessary for the musculature and the mantle cavity), which would explain the macroevolutionary tendency presented at the beginning of this section as well. Contrary, the transformations of PC2 and PC3 in this specimen may point to a more complex picture regarding Buckman’s first rule of covariation, implying that these transformations could be related to the development of reproductive structures, maturity, or sexual dimorphism, which would also explain why this pattern is relevant in closely related taxa such as the two species of Maorites. However, currently, there is no clear explanation for Buckman’s rules of covariation suggesting either an ecologic or morphogenetic driver (Monnet et al., 2015c), or even if it is a frequent pattern or is restricted to specific taxa. The transformations included in PC2 and PC3 may be important to determine the origin of this covariation pattern as more data become available, particularly from studying the ontogeny of closely related taxa.

In summary, the basic morphospace constructed in this work provides a first overview of the wide variation found in the ammonoid whorl shapes. Further, the biological patterns exhibit here should be validated by increasing the number of specimens (around 300 to 600 to be compared with other morphospaces), and further research is required to evaluate how the changes of the whorl-cross section determine the geometry of the conch, and as follows, their ecological properties. About the modelling technique applied to ammonoids, high-resolution images of cross-sections and tomographic data are the most suitable. Yet, this data is still scarce, and heavily skewed among groups, as different authors prioritized other features and traditional morphometrics to study the ammonoid conch (Bardin et al., 2014). Accordingly, if possible, these empirical data are preferred over diagrammatic sketches to reduce cognitive biases (Blanco, 2017) and should be added to the species description to generate accurate models.

CONCLUSIONS

Results demonstrate that the virtual modelling method described herein is a viable option to study the shape of the whorl cross-section in ammonoids using geometric morphometrics.

The variation of the whorl cross-section in ammonoids is mainly explained by three principal components that comprise a complex morphospace, exhibiting several cases of homeomorphy and clustering. The patterns of variations found indicate morphological changes associated to long-term evolutionary trends, and independent secondary changes observed in closely related taxa and/or maturity.

ACKNOWLEDGMENTS

The authors thank M.J. Royo y Gómez (Servicio Geológico Colombiano, Bogotá, Colombia) for giving access to some of the specimens used in this study. M.C. Rodríguez Amenábar (Instituto Antártico Argentino, Buenos Aires, Argentina) and M. Tanuz (Universidad de Buenos Aires, Buenos Aires, Argentina) are thanked for the loan of specimens under their care. Thanks to the Clínica La Sagrada Familia (Buenos Aires, Argentina) and its staff, where some of the CT-scan studies were accomplished. Special thanks to the cephalopod research community for the free access to additional data required for the analyses. We also thank the anonymous reviewers for their commentaries that significantly improved the manuscript. This is the contribution R-382 to the Instituto de Estudios Andinos ‘Don Pablo Groeber’ (IDEAN, UBA-CONICET).

REFERENCES

Adams, D.C., Rohlf, F.J., and Slice, D.E. 2004. Geometric morphometrics: ten years of progress following the ‘revolution’. Italian Journal of Zoology, 71:5-16. https://doi.org/10.1080/11250000409356545

Adams, D.C. and Otarola-Castillo, E. 2013. Geomorph: an R package for the collection and analysis of geometric morphometric shape data. Methods in Ecology and Evolution, 4:393-399. https://doi.org/10.1111/2041-210X.12035

Allen, E.G. 2016. New approaches to fourier analysis of ammonoid sutures and other complex, open curves. Paleobiology, 32:299-315. https://doi.org/10.1666/04042.1

Bardin, J., Rouget, I., and Cecca, F. 2014. Cladistics in ammonoids: back to the future. Neues Jahrbuch für Geologie und Paläontologie - Abhandlungen, 274:239-253. https://doi.org/10.1127/njgpa/2014/0449

Barrande, J. 1865. Systême silurien du centre de Ia Bohême, II, Classe des Mollusques, ordre des Cephalopodes, p. 1-107. In Barrande, J. (ed.), Systême silurien du Centre de la Bohême: 1ère. Partie: Recherches paléontologiques. M.M. Gottlieb Haase fils, Prague, Czech Republic.

Becker, R.T. 1995. Taxonomy and evolution of Late Famennian Tornocerataceae (Ammonoldea). Berliner Geowissenschafltiche Abhandlungen Reihe, 16:607-643.

Bersac, S. and Bert, D. 2012. Ontogenesis, variability and evolution of the Lower Greensand Deshayesitidae (Ammonoidea, Lower Cretaceous, Southern England): reinterpretation of literature data; taxonomic and biostratigraphic implications. Annales du Muséum d'Histoire Naturelle de Nice, 27:197-270.

Bersac, S. and Bert, D. 2020. The heteromorph ammonite genus Ancyloceras (Ancyloceratidae) in the Paris Basin (lower Aptian, Lower Cretaceous, NE France). Annales de Paléontologie, 106:1-59. https://doi.org/10.1016/j.annpal.2019.102365

Bischof, E.A., Schlüter, N., Korn, D., and Lehmann, J. 2021. Ontogeny of highly variable ceratitid ammonoids from the Anisian (Middle Triassic). PeerJ, 9e10931:1-26. https://doi.org/10.7717/peerj.10931

Blanco, F. 2017. Cognitive bias, p. 1-7. In Vonk, J. and Shackelford, T. (eds.), Encyclopedia of Animal Cognition and Behavior. Springer International Publishing, Cham. https://doi.org/10.1007/978-3-319-47829-6_1244-1

Blender Online Community 2021. Blender, a 3D Modelling and Rendering Package.
https://www.blender.org/download/releases/2-81/

Bogoslovsky, B.I. 1971. Devonskie ammonoidei. II. Goniatity. Trudy faleontologicheskogo Instituta Akade- miya Nauk SSS, 127:1-228.

Brayard, A. and Bucher, H. 2008. Smithian (Early Triassic) ammonoid faunas from northwestern Guangxi (South China): Taxonomy and Biochronology. Fossils and Strata, 55:1-184.

Burnaby, T.P. 1966. Allometric growth of ammonoid shells: a generalization of the logarithmic spiral. Nature, 209:904-906. https://doi.org/10.1038/209904b0

Catmull, E. and Clark, J. 1978. Recursively generated B-spline surfaces on arbitrary topological meshes. Computer-Aided Design, 10:350-355. https://doi.org/10.1016/0010-4485(78)90110-0

Chao, K. 1959. Lower Triassic ammonoids from Western Kwangsi, China. Palaeontologia Sinica, New Series B, 9:1-355.

Checa, A. 1991. Sectorial expansion and shell morphogenesis in molluscs. Lethaia, 24:97-114. https://doi.org/10.1111/j.1502-3931.1991.tb01183.x

Chlupáč, I. and Turek, V. 1983. Devonian goniatites from the Barrandian area, Czechoslovakia. Rozpravy Ústředního ústavu geologického, 46:1-153.

Claude, J. 2008. Morphometrics with R. Springer, New York, NY. https://doi.org/10.1007/978-0-387-77789-4

Collignon, M. 1971. Atlas des fossiles caractéristiques de Madagascar (Ammonites) XVII (Maestrichtien). Tananarive: Service Géologique, 4:1-44.

Courville, P. and Crônier, C. 2016. Diversity or disparity in the Jurassic (Upper Callovian) genus Kosmoceras (Ammonitina): a morphometric approach. Journal of Paleontology, 79:944-953.
https://doi.org/10.1666/0022-3360(2005)079[0944:DODITJ]2.0.CO;2

De Baets, K., Klug, C., and Monnet, C. 2013. Intraspecific variability through ontogeny in early ammonoids. Paleobiology, 39:75-94. https://doi.org/10.1666/0094-8373-39.1.75

De Baets, K., Bert, D., Hoffmann, R., Monnet, C., Yacobucci, M.M., and Klug, C. 2015. Ammonoid intraspecific variability, p. 359-426. In Klug, C., Korn, D., De Baets, K., Kruta, I., and Mapes, R.H. (eds.), Ammonoid Paleobiology: From Anatomy to Ecology. Topics in Geobiology, vol 43. Springer Netherlands, Dordrecht. https://doi.org/10.1007/978-94-017-9630-9_9

Ebbighausen, V. and Bockwinkel, J. 2007. Tournaisian (Early Carboniferous/Mississippian) ammonoids from the Ma'der Basin (Anti-Atlas, Morocco). Fossil Record, 10:125-163. https://doi.org/10.1002/mmng.200700003

Ebbighausen, V., Korn, D., and Bockwinkel, J. 2010. The ammonoids from the Dalle à Merocanites of Timimoun (Late Tournaisian-Early Viséan; Gourara, Algeria). Fossil Record, 13:153-202. https://doi.org/10.1002/mmng.200900011

Ebbighausen, V., Becker, R., and Bockwinkel, J. 2011. Emsian and Eifelian ammonoids from Oufrane, eastern Dra Valley (Anti-Atlas, Morocco) - taxonomy, stratigraphy and correlation. Neues Jahrbuch für Geologie und Paläontologie - Abhandlungen, 259:313-379. https://doi.org/10.1127/0077-7749/2011/0121

Erlich, A., Moulton, D.E., Goriely, A., and Chirat, R. 2016. Morphomechanics and developmental constraints in the evolution of ammonites shell form. Journal of Experimental Zoology Part B: Molecular and Developmental Evolution, 326:437-450. https://doi.org/10.1002/jez.b.22716

Foxon, F. 2021. Ammonoid taxonomy with supervised and unsupervised machine learning algorithms. paleorxiv.org:1-13. https://doi.org/10.31233/osf.io/ewkx9

Frech, F. 1887. Die paläozoischen Bildungen von Cabrières (Languedoc). Zeitschrift der Deutschen Geologischen Gesellschaft, 39:360-487.

Fucini, A. 1901. Cefalopodi liassici del Monte di Cetona. Parte prima. Palaeontographia Italica: Memoria di Paleontologia, 7:1-89.

Gemmellaro, G.G. 1872-1882. Sopra i Cephalopodi della zona con Stephanoceras macrocephaum (Schlot.) della Rocca chi Parra presso Calatafimi, Provincia dei Trapani, Sicilia. Atti del Accademia gioenia di Scienze Natural, 3:5-30.

Gerber, S. 2017. The geometry of morphospaces: lessons from the classic Raup shell coiling model. Biological Reviews Cambridge Philosophical Society, 92:1142-1155. https://doi.org/10.1111/brv.12276

Girty, G.H. 1909. The fauna of the Caney Shale of Oklahoma, Bulletin of the U.S. Geological Survey, 377:1-106.

Hammer, Ø. and Bucher, H. 1999. Reaction-diffusion processes: application to the morphogenesis of ammonoid ornamentation. Geobios, 32:841-852. https://doi.org/10.1016/S0016-6995(99)80866-3

Hammer, Ø., Harper, D., and Ryan, P. 2001. PAST: Paleontological statistics software package for education and data analysis. Palaeontologia Electronica, 4:1-9. https://palaeo-electronica.org/2001_1/past/issue1_01.htm

Hebdon, N., Ritterbush, K., and Choi, Y. 2020. Computational fluid dynamics modeling of fossil ammonoid shells. Palaeontologia Electronica, 23(1):a21. https://doi.org/10.26879/956

Hoffmann, R. 2010. New insights on the phylogeny of the Lytoceratoidea (Ammonitina) from the septal lobe and its functional interpretation. Revue de Paléobiologie, 29:1-156.

Hoffmann, R., Morón-Alfonso, D.A., Klug, C., and Tanabe, K. 2021. Ammonoid soft tissue remains revealed by computed tomography. Swiss Journal of Palaeontology, 140:1-11. https://doi.org/10.1186/s13358-021-00226-y

Hohenegger, J. and Tatzreiter, F. 1992. Morphometric methods in determination of ammonite species, exemplified through Balatonites shells (Middle Triassic). Journal of Paleontology, 66:801-816. https://doi.org/10.1017/S0022336000020813

Hyatt, A. 1883-1884. Genera of fossil cephalopods. Proceedings of the Boston Society of Natural History, 1:253-338.

Jacob, C. 1907. Étude sur quelques ammonites du Crétacé moyen. Société Géologique de France, 38:5-63.

Jolliffe, I. and Cadima, J. 2016. Principal component analysis: a review and recent developments. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 374:1-16. https://doi.org/10.1098/rsta.2015.0202

Kakabadze, M.V. 1981. Antsilotseratidy yuga SSSR i ikh stratigraphicheskoe znachenie (Ancyloceratids of the south of the USSR and their stratigraphical significance). Trudy Gelogicheskogo Instituta Akademii Nauk GSSR (novaya seriya), 71:1-195.

Kakabadze, M.V. and Hoedemaeker, P.J. 2004. Heteromorphic ammonites from the Barremian and Aptian strata of Colombia. Scripta Geologica, 128:39-182.

Kendall, D.G. 1984. Shape manifolds, procrustean metrics, and complex projective spaces. Bulletin of the London Mathematical Society, 16:81-121. https://doi.org/10.1112/blms/16.2.81

Kennedy, W.J. and Klinger, H. 1875. Cretaceous faunas from Zululand and Natal, South Africa. The family Lytoceratidae Neumayr. Annals of the South African Museum, 74:257-333.

Kennedy, W.J. and Klinger, H. 2012. Cretaceous faunas from Zululand and Natal, South Africa. New records of Maastrichtian ammonites of the Family Kossmaticeratidae. African Natural History, 9:55-60.
http://www.scielo.org.za/scielo.php?script=sci_arttext&pid=S2305-79632013000100003

Kennedy, W.J., Crame, J.A., Bengtson, P., and Thomson, M.R.A. 2007. Coniacian ammonites from James Ross Island, Antarctica. Cretaceous Research, 28:509-531. https://doi.org/10.1016/j.cretres.2006.08.006

Kilian, W. and Reboul, P. 1909. Les Cephalopodes neocretacées des Iles Seymour et Snow Hill. Wissenschaftliche Ergebnisse der Schwedischen Südpolar-Expedition 1901-1903, Stockholm, 3:1-75.

Klein, C. and Korn, D. 2014. A morphometric approach to conch ontogeny of Cymaclymenia and related genera (Ammonoidea, Late Devonian). Fossil Record, 17:1-32. https://doi.org/10.5194/fr-17-1-2014

Klug, C. 2002. Quantitative stratigraphy and taxonomy of late Emsian and Eifelian ammonoids of the Anti-Atlas (Morocco). CFS Courier Forschungsinstitut Senckenberg, 238:1-109.

Klug, C., Korn, D., Landman, N.H., Tanabe, K., De Baets, K., and Naglik, C. 2015. Describing ammonoid conchs, p. 3-24. In Klug, C., Korn, D., De Baets, K., Kruta, I., and Mapes, R.H. (eds.), Ammonoid Paleobiology: From Anatomy to Ecology. Topics in Geobiology, vol 43. Springer Netherlands, Dordrecht. https://doi.org/10.1007/978-94-017-9630-9_1

Korn, D. 1997. The Palaeozoic ammonoids of the South Portuguese Zone. Memorias do Instituto geologico e Mineiro, 33:1-131.

Korn, D. 1999. Famennian ammonoid stratigraphy of the Ma'der and Tafilalt (Eastern Anti-Atlas, Morocco). Abhandlungen der Geologischen Bundesanstalt, 54:147-179.

Korn, D. 2010. A key for the description of Palaeozoic ammonoids. Fossil Record, 13:5-12. https://doi.org/10.1002/mmng.200900008

Korn, D. and Klug, C. 2002. Ammoneae Devonicae, p. 1-375. In Leiden, B. (ed.), Fossilium Catalogus. Animalia. Leiden: Backhuys, Kerkwerve, Netherlands.

Korn, D. and Klug, C. 2012. Palaeozoic ammonoids-diversity and development of conch morphology, p. 491-534. In Talent, J.A. (ed.), Earth and Life: Global Biodiversity, Extinction Intervals and Biogeographic Perturbations Through Time. Springer Netherlands, Dordrecht. https://doi.org/10.1007/978-90-481-3428-1_15

Korn, D., Bockwinkel, J., and Ebbighausen, V. 2010. The ammonoids from the Argiles de Teguentour of Oued Temertasset (early Late Tournaisian; Mouydir, Algeria). Fossil Record, 13:35-152. https://doi.org/10.1002/mmng.200900010

Kutygin, R. 2003. Paratumaroceras, a new paragastrioceratid genus (Ammonoidea) from the Lower Permian of the western Verkhoyansk Region. Paleontological Journal, 37:252-256.

Leonova, T. 1989. Systematic paleontology, in Rannepermskie ammonoidei Yugo-Vostochnogo Pamira. Akademiya Nauk SSSR, Trudy Paleontologicheskogo Instituta, 235:1-198.

Leonova, T.B. 2011. Permian ammonoids: biostratigraphic, biogeographical, and ecological analysis. Paleontological Journal, 45:1206-1312. https://doi.org/10.1134/S0031030111100029

Leonova, T.B. and Boiko, M.S. 2011. Revision of the Permian ammonoid family Thalassoceratidae Hyatt. Paleontological Journal, 45:599-608. https://doi.org/10.1134/S0031030111060086

Levin, M., Anavy, L., Cole, A.G., Winter, E., Mostov, N., Khair, S., Senderovich, N., Kovalev, E., Silver, D.H., Feder, M., Fernandez-Valverde, S.L., Nakanishi, N., Simmons, D., Simakov, O., Larsson, T., Liu, S.-Y., Jerafi-Vider, A., Yaniv, K., Ryan, J.F., Martindale, M.Q., Rink, J.C., Arendt, D., Degnan, S.M., Degnan, B.M., Hashimshony, T., and Yanai, I. 2016. The mid-developmental transition and the evolution of animal body plans. Nature, 531(7596):637-641. https://doi.org/10.1038/nature16994

Macellari, C.E. 1986. Late Campanian-Maastrichtian ammonite fauna from Seymour Island (Antarctic Peninsula). Journal of Paleontology, 60:1-55. https://doi.org/10.1017/S0022336000060765

Matern, H. 1931. Das Oberdevon der Dill-Mulde. Abhandlungen der preußischen Geologischen Landesanstalt, Neue Folge, 134:1-139.

Mojsisovics, E.V. 1869. Ueber die Gliederung der oberen Triasbildungen der östlichen Alpen. Jahrbuch der geologischen Reichsanstalt Wien, 19:91-150.

Monnet, C. and Bucher, H. 2005. New Middle and Late Anisian (Middle Triassic) ammonoid faunas from northwestern Nevada (USA): taxonomy and biochronology. Fossils and Strata, 52:1-121.

Monnet, C., Brayard, A., and Brosse, M. 2015a. Evolutionary trends of Triassic ammonoids, p. 25-50. In Klug, C., Korn, D., De Baets, K., Kruta, I., and Mapes, R.H. (eds.), Ammonoid Paleobiology: From Macroevolution to Paleogeography. Topics in Geobiology, vol 43. Springer Netherlands, Dordrecht. https://doi.org/10.1007/978-94-017-9633-0_2

Monnet, C., De Baets, K., and Yacobucci, M.M. 2015b. Buckman’s rules of covariation, p. 67-94. In Klug, C., Korn, D., De Baets, K., Kruta, I., and Mapes, R.H. (eds.), Ammonoid Paleobiology: From Macroevolution to Paleogeography. Topics in Geobiology, vol 43. Springer Netherlands, Dordrecht. https://doi.org/10.1007/978-94-017-9633-0_4

Morón-Alfonso, D.A. 2019. Exploring the paleobiology of ammonoids (Cretaceous, Antarctica) using non-invasive imaging methods. Palaeontologia Electronica, 22.3.57:1-17. https://doi.org/10.26879/1007

Morón-Alfonso, D.A., Peterman, D.J., Cichowolski, M., Hoffmann, R., and Lemanis, R.E. 2020. Virtual 3D modeling of the ammonoid conch to study its hydrostatic properties. Acta Palaeontologica Polonica, 65:467-480. https://doi.org/10.4202/app.00776.2020

Moseley, H. 1838. XVII. On the geometrical forms of turbinated and discoid shells. Philosophical Transactions of the Royal Society of London, 128:351-370. https://doi.org/10.1098/rstl.1838.0018

Moulton, D.E., Goriely, A., and Chirat, R. 2015. The morpho-mechanical basis of ammonite form. Journal of Theoretical Biology, 364:220-230. https://doi.org/10.1016/j.jtbi.2014.09.021

Naglik, C., Tajika, A., Chamberlain, J., and Klug, C. 2015. Ammonoid locomotion, p. 649-688. In Klug, C., Korn, D., De Baets, K., Kruta, I., and Mapes, R.H. (eds.), Ammonoid Paleobiology: From Anatomy to Ecology. Topics in Geobiology, vol 43. Springer Netherlands, Dordrecht. https://doi.org/10.1007/978-94-017-9630-9_17

Neige, P. 1999. The use of landmarks to describe ammonite shape, p. 263-272. In Olóriz, F. and Rodríguez-Tovar, F.J. (eds.), Advancing Research on Living and Fossil Cephalopods. Springer US, Boston. https://doi.org/10.1007/978-1-4615-4837-9_20

Niebuhr, B., Taherpour Khalil Abad, M., Wilmsen, M., Razmi, J.N., Aryaei, A.A., and Ashouri, A. 2016. First record of late Campanian ammonites from the Abderaz Formation of the Koppeh Dagh, northeastern Iran. Cretaceous Research, 58:202-222. https://doi.org/10.1016/j.cretres.2015.10.006

Okamoto, T. 1988. Analysis of heteromorph ammonoids by differential geometry. Palaeontology, 31:35-52.

Okamoto, T. 1996. Theoretical modeling of ammonoid morphology, p. 225-251. In Landman, N.H., Tanabe, K., and Davis, R.A. (eds.), Ammonoid Paleobiology. Springer, Boston, MA. https://doi.org/10.1007/978-1-4757-9153-2_8

Orbigny, A.D. 1850. Prodrome de Paléontologie stratigraphique universelle des animaux mollusques et rayonnées, 2. Place de l'École de Médicine, Paris, France. https://doi.org/10.5962/bhl.title.45605

Parent, H., Bejas, M., Greco, A., and Hammer, Ø. 2012. Relationships between dimensionless models of ammonoid shell morphology. Acta Palaeontologica Polonica, 57:445-447. https://doi.org/10.4202/app.2010.0118

Paulcke, W. 1907. Die Cephalopoden der oberen Kreide Südpatagoniens. Berichte der Naturforschenden Gesellschaft zu Freiburg im Breisgau 15 (for 1905):167-224.

Pavia, G. and Fernandéz-López, S.R. 2019. Bajocian Lissoceratinae (Haploceratoidea, Ammonitida) from the Mediterranean-Caucasian Subrealm. Rivista Italiana di Paleontologia e Stratigrafia, 125:29-75. https://doi.org/10.13130/2039-4942/11058

Peterman, D., Ciampaglio, C., Shell, R., and Yacobucci, M. 2019a. Mode of life and hydrostatic stability of orthoconic ectocochleate cephalopods: hydrodynamic analyses of restoring moments from 3D printed, neutrally buoyant models. Acta Palaeontologica Polonica, 64:441-460. https://doi.org/10.4202/app.00595.2019

Peterman, D.J., Barton, C., and Yacobucci, M. 2019b. The hydrostatics of Paleozoic ectocochleate cephalopods (Nautiloidea and Endoceratoidea) with implications for modes of life and early colonization of the pelagic zone. Palaeontologia Electronica, 22.2.24A:1-29. https://doi.org/10.26879/884

Peterman, D.J., Hebdon, N., Ciampaglio, C.N., Yacobucci, M.M., Landman, N.H., and Linn, T. 2020. Syn vivo hydrostatic and hydrodynamic properties of scaphitid ammonoids from the U.S. Western Interior. Geobios, 60:79-98. https://doi.org/10.1016/j.geobios.2020.04.004

Raup, D.M. 1961. The geometry of coiling in gastropods. Proceedings of the National Academy of Sciences, 47:602-609. https://doi.org/10.1073/pnas.47.4.602

Raup, D.M. 1966. Geometric analysis of shell coiling: general problems. Journal of Paleontology, 40:1178-1190. https://www.jstor.org/stable/1301992

Raup, D.M. 1967. Geometric analysis of shell coiling: coiling in ammonoids. Journal of Paleontology, 41:43-65. https://www.jstor.org/stable/1301903

Raup, D.M. and Michelson, A. 1965. Theoretical morphology of the coiled shell. Science, 147:1294-1295. https://doi.org/10.1126/science.147.3663.1294

Riedel, L. 1938. Ammonitas del cretácico inferior de la Cordillera Oriental, p. 7-80. In Scheibe, E.A. (ed.), Estudios geológicos y paleontológicos sobre la Cordillera Oriental de Colombia, part 2. Departamento de Minas y Petróleos, Bogotá, Colombia.

Ritterbush, K. 2015. Interpreting drag consequences of ammonoid shells by comparing studies in Westermann Morphospace. Swiss Journal of Palaeontology, 135:125-138. https://doi.org/10.1007/s13358-015-0096-8

Ruzhencev, V.E. 1933. O nekotorykh nizhnepermskikh ammonoideyakh Aktyubinskogo rayona. Byulleten' Moskovskaya obshchestva ispytatelei prirody, otdelenie geologii, 11:164-180.

Ruzhencev, V.E. 1950. Verkhnekammenouglo'nye Ammonity Urala. Akademiya Nauk SSSR, Trudy Paleontologicheskogo Instituta, 29:1-223.

Ruzhencev, V.E. 1956. Nizhnepermskie ammonity yuzhnogo Urala II. Ammonity Artinskogo yarusa. Akademiya Nauk SSSR, Trudy Paleontologicheskogo Instituta, 60:1-127.

Sabin, M. 2002. Chapter 12 - Subdivision surfaces, p. 309-325. In Farin, G., Hoschek, J., and Kim, M.-S. (eds.), Handbook of Computer Aided Geometric Design. North-Holland, Amsterdam. https://doi.org/10.1016/B978-044451104-1/50013-7

Salazar, C., Stinnesbeck, W., and Quinzio-Sinn, L. 2010. Ammonites from the Maastrichtian (Upper Cretaceous) Quiriquina Formation, in central Chile. Neues Jahrbuch für Geologie und Paläontologie - Abhandlungen, 257:181-236. https://doi.org/10.1127/0077-7749/2010/0072

Sandberger, G. 1851. Beobachtungen über mehrere schwierige Puncte der Organisation der Goniatiten. Jahrbücher des Vereins für Naturkunde im Herzogthum Nassau, 7:292-304. 

Sandberger, G. 1853. Einige Beobachtungen über Clymenien; mit besonderer Rücksicht auf die westphälischen Arten. Verhandlungen des Naturhistorischen Vereines der Preussischen Rheinlande und Westphalens, 10:171-216.

Sandberger, G. 1857. Paläontologische Kleinigkeiten aus den Rheinlanden. Verhandlungen des Naturhistorischen Vereines der Preussischen Rheinlande und Westphalens, 14:140-142.

Saunders, W., Spinosa, C., Teichert, C., and Banks, R.C. 1978. The jaw apparatus of recent Nautilus and its palaeontological implications. Palaeontology, 21:129-141.

Saunders, W.B. and Andrew, R.H. 1984. Morphology and morphologic diversity of mid-Carboniferous (Namurian) ammonoids in time and space. Paleobiology, 10:195-28. https://www.jstor.org/stable/2400397

Savazzi, E. 1985. SHELLGEN: A BASIC program for the modeling of molluscan shell ontogeny and morphogenesis. Computers & Geosciences, 11:521-530. https://doi.org/10.1016/0098-3004(85)90083-4

Scasso, R.A., Prámparo, M.B., Vellekoop, J., Franzosi, C., Castro, L.N., and Sinninghe Damsté, J.S. 2020. A high-resolution record of environmental changes from a Cretaceous-Paleogene section of Seymour Island, Antarctica. Palaeogeography, Palaeoclimatology, Palaeoecology, 555:109844. https://doi.org/10.1016/j.palaeo.2020.109844

Schlager, S. 2017. Chapter 9 - Morpho and Rvcg-shape analysis in R: R-Packages for geometric morphometrics, shape analysis and surface manipulations, p. 217-256. In Zheng, G., Li, S., and Székely, G. (eds.), Statistical Shape and Deformation Analysis. Academic Press. https://doi.org/10.1016/B978-0-12-810493-4.00011-0

Smith, P.L. 1986. The implications of data base management systems to paleontology: a discussion of Jurassic ammonoid data. Journal of Paleontology, 60:327-340.

Spath, L.F. 1923. A monograph of the Ammonoidea of the Gault. Part I. Plates I-IV. Monographs of the Palaeontographical Society, 75:1-72. https://doi.org/10.1080/02693445.1923.12035588

Spath, L.F. 1930. On some Ammonoidea from the Lower Greensand. Annals and Magazine of Natural History, London, 10:417-464.

Steinmann, G. 1895. Die Cephalopoden der Quiriquina-Schichten. Neues Jahrbuch für Mineralogie, Geologie und Paläontologie, 10:64-94.

Tajika, A. and Klug, C. 2020. How many ontogenetic points are needed to accurately describe the ontogeny of a cephalopod conch? A case study of the modern nautilid Nautilus pompilius. PeerJ, 8:e8849:1-14. https://doi.org/10.7717/peerj.8849

Tajika, A., Naglik, C., Morimoto, N., Pascual-Cebrian, E., Hennhöfer, D., and Klug, C. 2015. Empirical 3D model of the conch of the Middle Jurassic ammonite microconch Normannites: its buoyancy, the physical effects of its mature modifications and speculations on their function. Historical Biology, 27:181-191. https://doi.org/10.1080/08912963.2013.872097

Tendler, A., Mayo, A., and Alon, U. 2015. Evolutionary tradeoffs, Pareto optimality and the morphology of ammonite shells. BMC Systems Biology, 9:1-12. https://doi.org/10.1186/s12918-015-0149-z

Tobin, T.S., Ward, P.D., Steig, E.J., Olivero, E.B., Hilburn, I.A., Mitchell, R.N., Diamond, M.R., Raub, T.D., and Kirschvink, J.L. 2012. Extinction patterns, δ¹⁸O trends, and magnetostratigraphy from a southern high-latitude Cretaceous-Paleogene section: links with Deccan volcanism. Palaeogeography, Palaeoclimatology, Palaeoecology, 350-352:180-188. https://doi.org/10.1016/j.palaeo.2012.06.029

Tomas, R. and Pálfy, J. 2007. Revision of Early Jurassic ammonoid types from the Perşani Mts. (East Carpathians, Romania). Neues Jahrbuch für Geologie und Paläontologie - Abhandlungen, 243:231-254. https://doi.org/10.1127/0077-7749/2007/0243-0231

Tozer, E.T. 1967. A standard for Triassic time. Geological Survey of Canada, 156:1-103.

Trueman, A.E. 1940. The ammonite body-chamber, with special reference to the buoyancy and mode of life of the living ammonite. Quarterly Journal of the Geological Society, 96:339-383. https://doi.org/10.1144/GSL.JGS.1940.096.01-04.14

Ubukata, T., Tanabe, K., Shigeta, Y., Maeda, H., and Mapes, R.H. 2008. Piggyback whorls: a new theoretical morphologic model reveals constructional linkages among morphological characters in ammonoids. Acta Palaeontologica Polonica, 53:113-128. https://doi.org/10.4202/app.2008.0108

Urdy, S., Goudemand, N., Bucher, H., and Chirat, R. 2010. Allometries and the morphogenesis of the molluscan shell: a quantitative and theoretical model. Journal of Experimental Zoology. Part B, Molecular and Developmental Evolution, 314:280-302. https://doi.org/10.1002/jez.b.21337

Vöhringer, E. 1960. Die Goniatiten der unterkarbonischen Gattendorfia-Stufe im Hönnetal (Sauerland). Fortschritte in der Geologie von Rheinland und Westfalen, 3:107-196.

Wani, R. and Ayyasami, K. 2009. Ontogenetic change and intra-specific variation of shell morphology in the Cretaceous nautiloid (Cephalopoda, Mollusca) Eutrephoceras clementinum (D'Orbigny, 1840) from the Ariyalur Area, Southern India. Journal of Paleontology, 83:365-378. https://doi.org/10.1666/08-119.1

Wani, R. and Mapes, R.H. 2010. Conservative evolution in nautiloid shell morphology: evidence from the Pennsylvanian nautiloid Metacoceras mcchesneyi from Ohio, USA. Journal of Paleontology, 84:477-492. https://doi.org/10.1666/09-158.1

Wegerer, M., De Baets, K., and Korn, D. 2018. Quantitative analysis of suture lines in Carboniferous ammonoids. Fossil Record, 21:223-236. https://doi.org/10.5194/fr-21-223-2018

Weller, S. 1903. The Stokes collection of Antarctic fossils. Journal of Geology, 11:413-419.

Westermann, G.E.G. 1954. Monographie der Otoitidae (Ammonoidea), Otoites, Trilobiticeras, Itinsaites, Epalxites, Germanites, Masckeites, Normannites. Beihefte zum Geologischen Jahrbuch, 15:1-364.

Westermann, G.E.G. 1996. Ammonoid life and habitat, p. 607-707. In Landman, N.H., Tanabe, K., and Davis, R.A. (eds.), Ammonoid Paleobiology. Topic in Geobiology, vol. 13. Springer US, Boston. https://doi.org/10.1007/978-1-4757-9153-2_16

Westermann, G.E.G. 2013. Hydrostatics, propulsion and life-habits of the Cretaceous ammonoid Baculites. Revue de Paleobiologie, 32:249-265.

Wetzel, W. 1950. Fauna und Stratigraphie der Württembergica-Schichten insbesondere Norddeutschlands. Palaeontographica, 99:63-120.

White, C.A. 1879. Paleontological papers no. 9: fossils of the Jura-Trias of southeastern Idaho. Bulletin of the United States Geological and Geographical Survey of the Territories, 5:105-117.

Wilmsen, M. and Nagm, E. 2019. Palaeobiology and evolutionary context of Angulithes mermeti, a streamlined early Late Cretaceous shallow-water nautiloid. Acta Palaeontologica Polonica, 64:831-894. https://doi.org/10.4202/app.00637.2019

Witts, J.D., Whittle, R.J., Wignall, P.B., Crame, J.A., Francis, J.E., Newton, R.J., and Bowman, V.C. 2016. Macrofossil evidence for a rapid and severe Cretaceous-Paleogene mass extinction in Antarctica. Nature Communications, 7:1-9.
https://doi.org/10.1038/ncomms11738