Cephalopod Hydrostatics

The hydrostatics of Paleozoic ectocochleate cephalopods (Nautiloidea and Endoceratoidea) with implications for modes of life and early colonization of the pelagic zone

David J. Peterman, Christopher C. Barton, and Margaret M. Yacobucci

Article number: 22.2.24
https://doi.org/10.26879/884
Copyright Paleontological Society, May 2019

Author biographies
Plain-language and multi-lingual abstracts
PDF version

Submission: 3 May 2018. Acceptance: 11 April 2019

{flike id=2521}

ABSTRACT

Understanding the hydrostatic properties of ectocochleate cephalopods is essential to study the functional morphology of their shells. The conditions for neutral buoyancy, static orientation of the living animal, and their hydrostatic stability are key factors to determine the physical relationships and constraints on cephalopod life habits and paleoecology. The hydrostatics of early orthoconic and cyrtoconic Paleozoic cephalopods were investigated by digitally reconstructing morphotypes within Nautiloidea and Endoceratoidea. Morphotypes were chosen from several traditional orders and include endogastric cyrtocones (Ellesmerocerida and Discosorida), exogastric cyrtocones (Oncocerida), and longi-orthocones (Orthocerida and Endocerida). The extant nautilid, Nautilus pompilius, was also modeled as a reference for the hydrostatics of the Paleozoic cephalopods. All cyrtocone models have similar hydrostatic stability to the Nautilus and only the ellesmerocerid was found to be negatively buoyant. The hydrostatics of the neutrally buoyant cyrtocones suggests that they behaved as relatively poor-swimming demersal or nekto-benthic predators. This mode of life aligns with the largely neritic distribution of individuals belonging to these clades in the Paleozoic. In contrast, the orthocones studied were all capable of neutral buoyancy, much more stable than the Nautilus model, and all had vertical syn vivo orientations in a static setting. The hydrostatic properties of these morphotypes and their largely pelagic distribution support their role as vertical migrants. However, adapically distributed cameral deposits and endosiphuncular deposits would reduce stability, easing deviation from a vertical orientation. These adaptations, along with dorsal color patterns on some species, suggest that active locomotion in orthocones may have been more important than previously thought.

David J. Peterman. Department of Earth and Environmental Sciences, Wright State University, Dayton, Ohio, United States of America. peterman.10@wright.edu
Christopher C. Barton. Department of Earth and Environmental Sciences, Wright State University, Dayton, Ohio, United States of America. chris.barton@wright.edu
Margaret M. Yacobucci. Department of Geology, Bowling Green State University, Bowling Green, Ohio, United States of America. mmyacob@bgsu.edu

Keywords: cephalopod; Ordovician; buoyancy; orientation; paleoecology; digital models

Peterman, David J., Barton, Christopher C., and Yacobucci, Margaret M. 2019. The hydrostatics of Paleozoic ectocochleate cephalopods (Nautiloidea and Endoceratoidea) with implications for modes of life and early colonization of the pelagic zone. Palaeontologia Electronica 22.2.24A 1-29. https://doi.org/10.26879/884
palaeo-electronica.org/content/2019/2521-cephalopod-hydrostatics

Copyright: May 2019 Paleontological Society.
This is an open access article distributed under the terms of Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0), which permits users to copy and redistribute the material in any medium or format, provided it is not used for commercial purposes and the original author and source are credited, with indications if any changes are made.
creativecommons.org/licenses/by-nc-sa/4.0/

INTRODUCTION

Paleozoic ectocochleate cephalopods include diverse and paleoecologically important higher taxa, two of which are the focus of this study: Nautiloidea and Endoceratoidea. Understanding the hydrostatic properties of their conches is essential to better understand their modes of life, especially during their initial liberation from the benthos and colonization of the pelagic zone during the Early Ordovician. The goals of the present work were to 1) create highly accurate, three-dimensional digital models of a range of early Paleozoic cephalopod morphotypes; 2) use these models to calculate key hydrostatic properties, including the conditions necessary to achieve neutral buoyancy, the static orientation and stability of the shell during life; and 3) interpret these hydrostatic properties in the context of these cephalopods’ paleoecology.

Ectocochleate cephalopod conches consist of a body chamber inhabited by the living animal and a phragmocone divided by septa into a series of progressively larger chambers (camerae) throughout ontogeny. The phragmocone functions as an apparatus to regulate weight and buoyancy. This structure becomes a passive gas float if cameral liquid is removed and replaced with gas. This decrease in mass allows the phragmocone to be positively buoyant and compensates for the negative buoyancy of the soft body and mineralized shell, which are denser than seawater. Neutral buoyancy is achieved when the total mass of the organism is equal to the mass of the displaced seawater (following Archimedes’ principle). The static orientation of an object occurs when the centers of buoyancy and gravity are aligned vertically, while the object's stability is dependent upon their degree of separation (Okamoto, 1996; Westermann, 1998). Hydrostatic stability is quantified by the stability index (the distance between the centers of buoyancy and gravity normalized by the cube root of the organismal volume). Earlier studies have assumed the center of gravity to coincide with the center of the body chamber (Trueman, 1941; Raup, 1967; Raup and Chamberlain, 1967; Okamoto, 1996). This belief is largely due to the difficulty of computing accurate volumes and the total mass distribution. The stability indices derived by previous authors are proportionate to the results of the current study in the sense that larger values represent larger restoring moments to the equilibrium condition. Stability values quantify the resistance to wave action or ease/difficulty in modifying syn vivo orientation via active locomotion. A stability index of zero represents a scenario where the centers of buoyancy and gravity coincide, and there is no preferred orientation (similar to an object in zero gravity). Larger stability values will result in larger restoring moments acting to return the object to its static equilibrium condition. However, no studies have tested the magnitude of hydrodynamic restoration for cephalopods with different stability indices. Therefore, stability indices in the current study are relative to each other and the extant ectocochleate analogue, Nautilus pompilius.

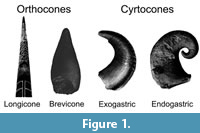While there is much variability in shell morphology throughout the evolutionary history of these cephalopods, only early Paleozoic cyrtocones and orthocones (curved and straight conches, respectively; Figure 1) were investigated here. The hydrostatics of the extant nautilid, Nautilus pompilius, was used as a reference for these Paleozoic cephalopods. Specific taxa were chosen that best represent the putative nautiloid clades Ellesmerocerida, Orthocerida, Oncocerida, and Discosorida and the endoceratoid clade, Endocerida. Although there are varying degrees of disparity, common morphotypes that have wide-reaching implications for other taxa were selected for study.

Ordovician Biodiversification

The Great Ordovician Biodiversification Event marked a drastic morphological and taxonomic diversification of many marine organisms (Frey et al., 2004). Consequently, the nautiloids rapidly diversified and expanded their habitat from shallow, low latitude paleoenvironments to nearly all marine paleoenvironments around the globe (Kröger and Zhang, 2009). In the earliest Ordovician (beginning of the Tremadocian stage) only a single nautiloid clade, the Ellesmerocerida, existed. Their conches can be characterized as generally small (<10 cm), slightly curved, endogastric (that is, coiling toward the venter) cyrtocones with close septal spacing, and fewer small longiconic forms (Furnish and Glenister, 1964). The appearance of Ellesmerocerida in the Late Cambrian marked the first cephalopods with siphuncular characteristics that would have increased the transport capacity of cameral liquid, allowing replacement with gases (Mutvei et al., 2007; Kröger et al., 2011). Although these shell forms were not well adapted for jet-powered swimming (Furnish and Glenister, 1964; Westermann, 1998; Mutvei et al., 2007), they would have been able to reduce their weight relative to their buoyant force. Cephalopods following the characteristic ellesmerocerid morphotype during the early Ordovician were virtually absent from deep basinal settings and largely confined to shallow neritic habitats (Kröger et al., 2009).

In the mid-Tremadocian, the higher taxa Orthocerida, Endocerida, and others appeared and strongly diversified. Fossils of these groups can be found in more distal settings and black shales, and may be contemporaneous with the evolution of passive and/or active swimming in a pelagic habitat (see Kröger et al., 2009 for a list of occurrences and relative distributions of taxa). Orthocerida and Endocerida consist of mostly straight orthoconic conchs that can be much larger than the ellesmerocerids. In the case of the endocerids, it is common for species to reach several meters in length, making them the largest swimming organisms in the Ordovician (Teichert and Kummel, 1960). One striking difference between the orthocerids and endocerids, aside from size, is the much larger siphuncle with common mineralized endosiphuncular deposits within the cones of Endocerida (Teichert, 1964a). Cameral deposits are commonly found within Orthocerida (and many other nautiloids), and their hydrostatic attributes were investigated by the use of three-dimensional (3D) modeling in this study. It has recently been suggested that cameral deposits in several species of Carboniferous coleoids may have formed post-mortem (Mutvei, 2018), which would invalidate cameral deposits being used as a hydrostatic device, at least in these groups. It is unclear, however, whether this finding applies to orthoconic nautiloids more broadly.

Oncocerida and Discosorida appeared in the Dapingian stage (early Middle Ordovician), and their fossils can be found within many shallow water depositional environments. Oncocerids are characterized by their small exogastrically curved (that is, coiling toward the dorsum) brevicones, while discosorids are generally endogastrically curved, like most ellesmerocerids. The oncocerids and discosorids have been dubbed the ecological successors of the ellesmerocerids due to their morphological similarities and occupation of mostly neritic habitats (Hewitt and Watkins, 1980; Kröger, 2007; Kröger and Zhang, 2009). They gradually began to replace ellesmerocerid taxa during the Middle Ordovician until they went extinct in the Late Ordovician. After several fluctuations of cephalopod biodiversity and much faunal turnover throughout the Ordovician, all remaining cephalopods suffered a biodiversity loss of nearly 70% during the Ordovician-Silurian mass extinction (Kröger, 2007).

Hydrostatic Experiments

Understanding the hydrostatic properties of key morphotypes is necessary in order to determine the physical relationships and constraints for Paleozoic cephalopod life habits, paleoecology, and evolution. Hydrostatic experiments of ectocochleate cephalopods were pioneered by Trueman (1941), who used two-dimensional (2D) median sections of ammonoids and measured volumes and densities of the phragmocone and body chamber. This approach is limited due to the complex interaction of bodies of differing densities on the true mass distribution. Isometric, empty planispiral shells were investigated by several authors (Raup, 1967; Raup and Chamberlain, 1967; Saunders and Shapiro, 1986; Swan and Saunders, 1987) but a neutrally buoyant condition always requires some volume of cameral liquid to occupy the phragmocone, unless the body chamber to phragmocone volume ratio perfectly compensates for the positive buoyancy of the phragmocone. The complex shape of shell ornamentation and septa (especially for ammonoids) must also be taken into account. Trueman (1941) found that the orthoconic ammonoid, Baculites, was very stable in a vertical orientation with the body chamber inclined downwards, an interpretation that has been commonly accepted since (Reyment, 1974; Ward, 1976; Westermann, 1977, 1996, 2013; Klinger, 1980). In terms of hydrostatics, these models can be regarded as close analogues to orthoconic nautiloids (although without cameral deposits and with much more complexly folded septa). Westermann (1977) experimented with several 2D hydrostatic models representing simplified orthocerids. He used phragmocone “counterweights” of differing densities, including cameral deposits and cameral liquid. These counterweights supplied a condition where the center of gravity was very slightly displaced ventrally under the center of buoyancy to allow a horizontal orientation. Body chamber length, which changes the mass distribution and capacity for a neutrally buoyant combination of cameral liquid and gas in the phragmocone, was investigated by Westermann (1977). For planispiral ectocochleate cephalopods, body chamber length inversely correlates with hydrostatic stability (i.e., the degree of resistance to deviation from a stable orientation) for a number of different taxa (Saunders and Shapiro, 1986; Okamoto, 1996).

Tomographic methods have recently been employed to produce accurate 3D volumes for use in buoyancy calculations (Hoffmann et al., 2014, 2018; Lemanis et al., 2015, 2016; Naglik et al., 2015a, 2015b, 2016; Tajika et al., 2015). Three-dimensional models of cephalopod shells have been generated by the use of CT scanning, allowing measurements of shell and chamber volumes that can be used in hydrostatic/buoyancy computations (Hoffmann et al., 2015, 2018; Lemanis et al., 2015). The CT scanning method, however, requires a sufficient density contrast between the object and surrounding matrix as well as access to CT scanning equipment. Serial grinding tomography, creating a 3D stack of images from 2D physical slices through the object, has been successfully used in morphometry and volumetry (Naglik et al., 2015a, 2015b) and even hydrostatic computations (Tajika et al., 2015; Naglik et al., 2016) for ammonoids. The drawbacks of the serial grinding tomography method are that it results in the loss of the specimen and is rather time consuming. Both methods require mostly complete, undeformed specimens with high contrasts (either optically or by density) between the fossil and surrounding matrix. These requirements are difficult to meet for Paleozoic cephalopod specimens, which are commonly preserved as steinkerns, have been deformed, or are incomplete (as is the case for many orthocones). Theoretical virtual models like those presented here can therefore serve as an alternative in cases of incomplete/rare specimens or those that are difficult to digitize.

Most hydrostatic experiments are limited by the difficulty in computing accurate volumes for each material that influences the mass distribution in an object (i.e., any material of unique density). Each of these materials has its own center of mass, which is weighted according to its density and spatial distribution of volume. Two-dimensional models cannot always account for these three-dimensional properties, and ignoring the architecture of the shell, septa, and materials that occupy them further distorts their accuracy. Two-dimensional models also assume perfect symmetry of the shell, which is not always true (Yacobucci and Manship, 2011). The accurate computation of the magnitude and distribution of these volumes is necessary to truly understand the conditions for neutral buoyancy, syn vivo orientation, and hydrostatic stability. Because complete nautiloid specimens are extremely rare and certain model parameters (shell/septum thickness, septal spacing, degree of taper, soft body morphology, and allometry) are variable, unpredictable, or not known, it is helpful to utilize theoretical 3D models. Hence, the work presented here sought to improve upon previously published hydrostatic models by constructing detailed, accurate digital 3D models of a range of Paleozoic cephalopod shell morphotypes and using them to compute the hydrostatic properties of these forms.

METHODS

Overview of 3D Modeling Approach and Model Components

Any ectocochleate cephalopod shell can be constructed by the use of an array generation tool (or several array instructions in a piecewise manner) in the open-source computer graphics software, Blender 2.76 (Blender Online Community, 2017). The array generation tool can be used to duplicate an object, then scale, rotate, and translate it in a similar manner to the morphospace instructions of Raup (1966). In this case, a whorl section served as the object to duplicate with an array, and after the desired shape was generated, these 2D whorl sections were bridged together to create a 3D tessellated triangular mesh in.stl format. As the number of duplicated whorl sections per whorl approaches infinity, the shell becomes perfectly smooth. Since file size is always a limitation, the total number of duplicated whorl sections for each model varied between 400 and 650. Identical array instructions were then applied to a smaller whorl section to create the inner surface of the shell by setting the size difference of the two whorl sections to the desired shell thickness.

Septa were constructed with the same array instructions in a similar manner to the shell. This approach duplicated the same number of septa as whorl sections for each model. To create a model with the correct number of septa, the extra septa were then deleted until they reached the measured septal spacing of each real specimen that the model represents. Septal spacing was assumed to be isometric throughout the phragmocone. Isometric septa are necessary to model the liquid and gas held in the camerae because the contents of the shell (3D meshes of cameral liquid and gas) are later replicated with the same array instructions. Nautiloid and endoceratoid septa were simply modeled as a fraction of a sphere after measuring the radius of curvature from a particular specimen in cross-section. Septal thickness was defined in Blender by use of the extrusion tool (even thickness solidification of an infinitely thin mesh to create a 3D object). During this process, the 2D triangles that compose the mesh were duplicated and translated with a specified offset (thickness) and direction. Blender also has an “even thickness” option during the extrusion process which was used to correct model inconsistencies in the current study. The array tool was applied to extruded septa so that thickness was consistently an identical function of whorl height.

Siphuncles were modeled in a similar manner to the shell, but the transverse cross-sectional dimensions were duplicated instead of the whorl section. The septal foramen was constructed by performing Boolean operations in the mesh repair software, Netfabb 2017.3 (Autodesk Inc., 2017b). The 3D mesh of the siphuncle was simply subtracted from the 3D mesh of the shell to create a foramen for the siphuncle to pass through.

The body chamber was constructed by deleting all model components except for the inner interface of the shell and the adoral interface of the terminal septum, then closing the aperture (with a flat fill in all Paleozoic models herein). Since soft body preservation in Paleozoic cephalopods is largely unknown (Teichert, 1964b; Westermann, 1998), all 3D meshes of the soft tissues are exclusively confined to the body chamber (simulating complete retraction of the soft body).

All models and their components were repaired with the extended repair feature in Netfabb 2017.3 (Autodesk Inc. 2017b) in order to fix model inconsistencies, open meshes, duplicated vertices, and overlapping or inverted faces. This produced manifold 3D meshes, which are necessary to compute the centers of mass, volumes, and other geometrical measurements.

Model Parameters and Taxon Selection

It is common for Paleozoic cephalopod specimens to exhibit some sort of alteration from its original state (by either mechanical breakage, strain, or chemical alteration). This is especially true for longer and larger orthocones, which are very rarely found complete. These forms of alteration make it difficult to make the necessary measurements, or to employ other methods of digitization of fossil specimens (serial grinding tomography or CT scanning; Hoffmann et al., 2014, 2018; Lemanis et al., 2015, 2016; Naglik et al., 2015a, 2015b, 2016; Tajika et al., 2015; Inoue and Kondo, 2016). Hence, estimates of shell and septum thickness for the models presented here were derived from several measurements of a well-preserved aragonitic orthoconic nautiloid specimen (BSPG 2011 0006; Bayerische Staatssammlung für Paläontologie und Geologie, Munich, Germany) from the Carboniferous Buckhorn Asphalt Lagerstätte (Seuss et al., 2012; p. 377, fig. 3C). These measurements of shell thickness and septal thickness were averaged as a function of whorl height (2.77% and 1.66%, respectively) to be used in shell reconstruction, and were held constant among all Paleozoic 3D models in this study. There is probably some variation in shell and septum thickness within each individual or each higher taxon; however, accurate values for the taxa represented by each of the 3D models are largely unknown because most specimens on which the models are based are incomplete, or steinkerns. Nevertheless, some value of thickness is absolutely necessary for hydrostatic simulations. To better understand how the assumption of constant shell/septal thickness ratios influenced hydrostatic analyses, an isometric shell of Nautilus pompilius created by the current modeling technique was compared with a model generated from a CT-scanned specimen of the same species, in which the shell and septal thicknesses were not a perfect function of whorl height (Hoffmann et al., 2014).

Three-dimensional models were constructed for extant Nautilus pompilius and several Paleozoic cephalopods that represent the typical shell morphologies of the nautiloid higher taxa Ellesmerocerida and Orthocerida and the endoceratoid higher taxon, Endocerida. Two exogastric cyrtocone morphotypes that exhibit different body chamber length ratios and angles of shell curvature were chosen from the incredibly diverse Oncocerida. Discosorida was represented by one endogastric cyrtocone. Although there is much morphological variation within each of these groups, the chosen morphotypes are typical and therefore have implications for the hydrostatics of many taxa, some of which are clearly differentiated between the neritic and pelagic zones (Kröger et al., 2009). Table 1 provides the shell generation array instructions for each morphotype modeled.

Extant Nautilida. A hydrostatic 3D model of the extant Nautilus pompilius was constructed by recording several measurements of shell and septum thickness from a half cut adult shell from the Philippines. All thicknesses were recorded with digital calipers. Its whorl section was created in Blender 2.76 and mirrored about the sagittal plane. This complete 2D whorl section was duplicated with a shell generation array (Table 1) that closely approximates the geometry of the real shell. The 3D model is a perfect isometric shell using the adult whorl section. Shell and septum thicknesses are not perfect isometric functions of whorl height (Figure 1); however, this assumption is necessary for the generation of a working hydrostatic model. Since Nautilus pompilius is the only studied cephalopod herein with known soft body morphology, a functional 3D model of the soft body was incorporated into this shell (provided by Peter Minister). This soft body model of the Nautilus was spliced onto the 3D mesh of the living chamber by performing a simple Boolean unison in Netfabb 2017.3 (Autodesk Inc. 2017b). The spacing of the septa were closely approximated by importing a 2D image of the half cut shell into Blender 2.76 to be used as a stencil. This required ignoring the approximation of the last few septa (a common adult modification in ectocochleates). The siphuncle diameter was measured as a function of whorl height and duplicated with the shell generation array (Table 1). A similar model was constructed by using a CT scanned shell (specimen from Hoffmann et al., 2014; Lemanis et al., 2015, 2016), which was scaled to the same size as the isometric model (by length). The living chamber and camerae were isolated by removing the external shell and preserving the internal interface that represents these volumes.

Ellesmerocerida. The hydrostatics of the largely neritic shell form (Kröger et al., 2009) of an endogastric breviconic cyrtocone, Plectronoceras sp., was investigated by reconstructing a nearly complete figured specimen from Furnish and Glenister, (1964; p. K146, fig. 81) that is accompanied by a whorl section. A 2D scan of this plate was imported into 3D space in Blender 2.76 in order to use the shell taper and rotation factor as a stencil for the shell generation array (Table 1). The siphuncle was constructed by creating a circle with a radius of 16% whorl height (as recorded from Furnish and Glenister, 1964) at the terminal septum and duplicating it with the same shell generation array. Because specimens of Plectronoceras are very rare, and never completely preserved (Chen and Teichert, 1983), body chamber length is unknown. A possible minimum body chamber ratio was attained by assuming that the specimen of Plectronoceras figured in Furnish and Glenister (1964; p. K146, fig. 81) has a nearly complete body chamber with the aperture terminating where the specimen is adorally broken (body chamber length / total length = 40%). An additional model was constructed by adding septa until the model became neutrally buoyant.

Orthocerida. An orthocone with a circular whorl section and central siphuncle was constructed using, as a function of whorl height, the shell/septal thickness, septal spacing, septal radius, and siphuncle diameter of Carboniferous nautiloid specimen BSPG 2011 0006 (Seuss et al., 2012; p. 377, fig. 3C; likely a pseudorthoceratid). The whorl section was duplicated with an array that translated and scaled it to reconstruct the appropriate angle of taper for this specimen. Since growth of orthocones is not perfectly isometric, a secondary angle of taper was adopted from a reconstruction of the long-lived genus Geisonoceras (figured in Teichert, 1964b p. K33) to ensure that the shell would not reach unreasonable length or proportions. This approach yielded a shell 57 cm long, with a changing taper angle during the apical 7 cm. Since body chamber length is variable within orthocerids, it was held constant within the mesodome category at 33% total length (Westermann, 1977, 2013). In order to investigate the hydrostatic properties of a larger body chamber ratio, this parameter was later manipulated to 44% of total length by simply removing three septa and accommodating a new soft body 3D mesh in the larger living chamber.

Cameral deposits were fabricated from an isolated 3D mesh of the terminal camera in the orthocerid 3D model. This volume was reduced to equal the proportion of empty space in the phragmocone. The Boolean difference operation of Netfabb 2017.3 (Autodesk Inc., 2017b) was used to subtract this 3D mesh from the original 3D mesh of the terminal camera to produce relatively even mural, hyposeptal, and episeptal cameral deposits lining the camera. This mesh can then be duplicated with the same array used to build the shell to produce cameral deposits lining all camerae in the phragmocone, the sum of which will still equal the percent of the total cameral volume occupied by cameral deposits.

Asymmetrical cameral deposits were fabricated in the case of an orthocerid with a dorsally displaced siphuncle and ventrally formed cameral deposits, a relatively common feature within Pseudorthoceratoidea (Sweet, 1964). The camerae of the previous orthocerid 3D model were sheared in Blender 2.76, which moved their centers 12% of whorl height at each septal location in the dorsal direction. These cameral deposits were created with the same process as the symmetrical cameral deposits, but the volume reduction of the initial terminal camera 3D mesh was applied only underneath the siphuncle in the ventral direction.

Endocerida. The mesodomic shell of the orthocerid model was also used for the endocerid model in order to compare the influence of a large siphuncle with endosiphuncular deposits. The siphuncular diameter was reconstructed as 30% whorl height (similar to the Endoceras figured in Teichert, 1964a; p. K175). Another endocerid model was constructed to be more similar to a true Endoceras, which required modeling a more dorso-ventrally compressed shell, with ventrally displaced siphuncle, and closer septal spacing (Teichert, 1964a). The percentage of endosiphuncular deposits in an emptied phragmocone was computed with Equation 4 (below) in order to partition the densities of these two volumes. While endocerids are some of the largest organisms in the Paleozoic, possibly reaching 9m in length (Teichert and Kummel, 1960; Teichert, 1964a), the endocerid models generated herein are only 57 cm long. This small size does not influence hydrostatic properties since the mass distributions are all relative. However, scaling would influence hydrodynamic calculations, especially during rapid movement or drag force calculations.

Oncocerida. Two genera of the exogastric, cyrtoconic oncocerids were selected, Oonoceras and Euryrizocerina. The Oonoceras 3D model was reconstructed from specimens CGS SM 385, 386, 387, and 388, while the Euryrizocerina 3D models were reconstructed from specimens NML 21830, CGS SM 378, 379, and 384 (all figured in Manda and Turek, 2009). These taxa were chosen to investigate the hydrostatic influences of body chamber length and shell curvature, which were both larger in Euryrizocerina than Oonoceras, for this morphotype. Differences in the mass distributions of cameral gas and liquid in the phragmocone were nullified by filling the proper ratio of cameral gas volume to total cameral volume (Φ_gas; see Equation 2 below) in each camera for both models. This provided a condition where each camera had the same percentage of cameral liquid and cameral gas. The whorl sections of both models were constructed with whorl height to width ratios of 1.34. The siphuncles are ventrally displaced, with a diameter of 5.53% of whorl height.

Discosorida. The endogastric cyrtocone Phragmoceras was digitally reconstructed from Teichert (1964c; p. K339, figure 246). The immature whorl section (before the modified aperture in the adult stage) and the body chamber to phragmocone ratio were constructed from Westermann (1998; figure 20.13). Due to the broadly inflated siphuncular segments, two 3D meshes were constructed. One represents the thinner part of the siphuncle that passes through each septal foramen, and the other is the inflated portion within each camera. Both 3D meshes were duplicated with the shell generation array (Table 1) and then unified to produce a single model of the complete siphuncle. A common adult modification within the phragmoceratids is a somewhat unusually constricted aperture with a dorsally displaced opening for the soft body and a ventral hyponomic sinus (Teichert, 1964c). This structure was simulated by creating a mesh denoting a 2D apertural opening from the transverse section in Teichert (1964c). The “magnetize” function in Meshmixer 3.3 (Autodesk Inc., 2017a) was then used to pull the external shell toward the aperture mesh. The final shell was smoothed and mirrored in this same program in order to remove asymmetry and other imperfections.

Hydrostatic Computations

The completed 3D models were used to calculate key hydrostatic parameters (Table 2). Important geometric information can be gathered from files in the.stl format, including 3D mesh volume and centers of mass, which were calculated in MeshLab v1.3.3 (Cignoni and Ranzuglia, 2014). Three-dimensional meshes for each material of unique density (e.g., the shell, soft body, cameral liquid, and cameral gas) are necessary components to determine the conditions for neutral buoyancy as well as shell stability and orientation.

Computation of Phragmocone Filling to Achieve Neutral Buoyancy

The amount of cameral gas and liquid were adjusted in order to produce a neutrally buoyant condition. This is computed with a modification of Archimedes principle:

msb + msh +mcl + mcg = mwd

(1)

where m_sb is the mass of the soft body, m_sh is the mass of the shell, m_cl is the mass of cameral liquid, m_cg is the mass of cameral gas, and m_wd is the total mass of water displaced.

The ratio of the volume of cameral gas to total cameral volume (Φ_gas) can be found by setting Equation 1 in terms of density and volume, then solving for Φ_gas:

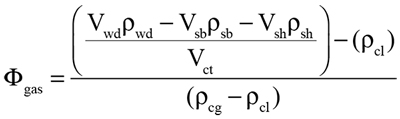(2)

where V_wd and P_wd are the volume and density of the water displaced by the whole model, V_sb and P_sb are the volume and density of the soft body, V_sh and P_sh are the volume and density of the shell, P_cl is the density of cameral liquid, P_cg is the density of cameral gas, and V_ct is the total volume of all camerae. The soft body density of 1.065 g/cm³ is implemented from Westermann (2013) and is assumed here to uniformly fill the body chamber. This value is averaged and considers the higher density of the mouthparts and lower density of the mantle cavity. This value is also applied to the siphuncle for all simulations, which has an approximately equal density to the soft body when uncalcified (Westermann, 1977). A shell density of 2.62 g/cm³ is commonly accepted (Reyment, 1958; Okamoto, 1996; Klug and Hoffmann, 2015) and is used herein. The density of cameral liquid is assumed to be equal to that of seawater (1.025 g/cm³; Greenwald and Ward, 1987), although this is slightly variable in life due to differences in salinity (Ward, 1979). The density of cameral gas is negligible, but used here for calculations as 0.001 g/cm³ (at standard temperature and pressure).

Equation 2 can be modified to solve for the percentage of available cameral volume occupied with cameral deposits (Φ_cd) by assuming the phragmocone is emptied of cameral liquid (that is, where Φ_gas = 100 %):

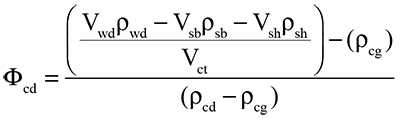(3)

where ρ_cd is the density of the cameral deposits (assumed to be equal to the density of the shell at 2.62 g/cm³).

The percentage of endosiphuncular deposits (Φed) in the siphuncle can be found by further modifying Equation 2 to allow the siphuncle model component to be partitioned into two segments of different densities:

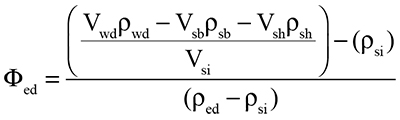(4)

where V_si and P_si are the volume and density (assumed to equal that of the soft body; 1.065 g/cm³) of the siphuncle, and P_ed is the density of the endosiphuncular deposits (assumed to equal that of the shell and cameral deposits; 2.62 g/cm³).

Computation of Stability and Orientation

The meshes of the shell, soft body, cameral deposits, endosiphuncular deposits, cameral gas, and cameral liquid each influence the mass distribution in different magnitudes according to their densities. The total center of gravity resulting from materials of differing positions, geometries, volumes, and densities can be calculated with the formula:

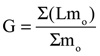(5)

where G is the x, y, or z component of the total center of gravity, L is the x, y, or z component of the center of gravity of a single object measured with respect to an arbitrary datum, and m_o is mass of any particular object that has a unique density.

The center of buoyancy B is essentially the center of the volume of the water displaced by the organism. This was found by generating a 3D mesh representing the exterior shell and soft body interfaces that encounter the water.

The stability of a model, that is, its degree of resistance to change in orientation, increases as the degree of separation between the centers of buoyancy and gravity increases. Okamoto (1996) used the center of the phragmocone and center of the living chamber as proxies for the centers of buoyancy and gravity, respectively. He also redefined the dimensionless stability index (S_t) of Raup (1967) in terms of the cube root of volume instead of shell diameter in order to apply the index to non-planispiral shell forms:

(6)

where S_t is the stability index,  is the distance between the true centers of buoyancy and gravity, and V is the entire volume occupied by the model (equal to V_wd defined above).

Finally, the static orientation of the animal under conditions of neutral buoyancy occurs when the centers of gravity and buoyancy are aligned vertically. This orientation can be expressed as the angle θ of the aperture’s inclination from vertical.

RESULTS

Nautilus pompilius 3D Hydrostatic Models

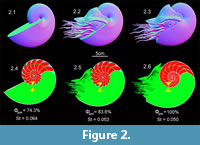In order to understand how the assumptions of isometry in coiling and shell/septal thickness (as a function of whorl height) affect the model’s hydrostatics, the isometric model of Nautilus pompilius (Figure 2.2 and 2.5) was compared with a CT-scanned shell (specimen from Hoffmann et al., 2014; Lemanis et al., 2015, 2016) of N. pompilius (Figure 2.3 and 2.6). The CT-scanned model had certain adult modifications (one slightly crowded septum, and a flared aperture) that increased the volume of water displaced, soft body, and shell when compared to the isometric model. The cameral volumes, however, remained relatively constant, which resulted in a larger percentage of emptied camerae (Φ_gas = 100.8%). This difference is also attributed to differing thicknesses of the real Nautilus shell (primarily a thicker umbilical region and thinning of septa towards the margins). Before scaling the CT scanned model to the same size (by length) as the isometric model, the shell mass computed with the methods of the current study is 212.6 g. This mass is only 4% different from the actual shell mass of 203.5 g presented in Hoffmann et al. (2014, pg. 2729, table 3) and suggests that the utilized methods and shell density of 2.62 g/cm³ can adequately represent the physical conchs. After normalizing by the respective masses of water displaced, the shell mass of the isometric model is 15.6% of the water displaced, while the CT-scanned model is 18.6% (Table 2). This difference very subtly influences the total mass distribution, yielding similar stability indices (St) for the isometric and CT-derived models (0.053 and 0.050, respectively; Figure 2.5 and 2.6). The percentage of soft body mass relative to mass of the water displaced by each model was also only slightly larger in the CT-scanned model (81.9% and 84.0%; Table 2).

The masses computed from each of these volumes are dependent upon the assumed density for each modeled object. The sensitivity of the computed Φ_gas and S_t to variations in assumed densities was evaluated for the CT-scanned Nautilus hydrostatic model by substituting lower and higher density estimates for the soft body and shell. The high density estimates for the soft body (1.068 g/cm³; Denton and Gilpin-Brown, 1966) and shell (2.98 g/cm³; Trueman, 1941; Raup and Chamberlain, 1967) resulted in 18.0% and 15.7% increases in Φ _gas and S_t, respectively (Table 3). However, these density estimates are rather high compared to other estimates (Hoffmann et al., 2015), do not consider the mantle cavity or buccal mass for the soft body, and assume the crystalline density of aragonite for the shell without organic components. The lower density estimates for the soft body (1.06 g/cm³; Westermann, 1977) and shell (2.53 g/cm³; Ebel, 1983) yield 7.4% and 7.7% reductions in Φ_gas and S_t, respectively (Table 3). The averaged soft body density of 1.065 g/cm³ used in the theoretical models of this study is applied to Paleozoic cephalopods because it considers the influence of the buccal mass, seawater, and the soft body. Little is known about the morphology of the buccal mass in early Paleozoic forms and the proportion of mantle cavity within the living chamber has been assumed to be similar to more recent cephalopods. The shell density used in this study considers nacreous aragonite and its organic components (2.62 g/cm³) and has been accepted by many previous workers (summarized in Hoffmann et al., 2015). Assuming that 20% of the body chamber is occupied by the mantle cavity, the averaged density when only considering the soft body (1.068 g/cm³) and seawater (1.025 g/cm³) is 1.059 g/cm³. This density difference of 0.006 g/cm³ accounts for a 0.56% difference from the values used in the current study. This percentage difference (by mass and volume) does not significantly affect the calculated total mass distribution. The hydrostatic influence of jaws, which are not known from Paleozoic cephalopod fossils before the Devonian (Kröger et al., 2011), is also very subtle according to these differences.

The hydrostatics of the isometric model of Nautilus pompilius were computed under two conditions: 1) the soft body retracted into the body chamber and flush with the aperture (Figure 2.1); and 2) an extended soft body closely exhibiting the morphology of this species (Figure 2.2). These two conditions were used to test the impact of the assumption that the soft body ended at the aperture, a necessary simplification, due to the unknown soft body morphology of the Paleozoic cephalopods in this study. With the soft body retracted, 74.3% of the phragmocone needs to be emptied to achieve a neutrally buoyant condition (Figure 2.4). For this condition to persist when adding the volume of the extended soft body, 83.6% of the phragmocone need be emptied (Figure 2.5). Therefore, the Paleozoic cephalopods that the later 3D models represent would require more of the phragmocone to be emptied than computed, and depend upon their unknown soft body morphologies. The stability index is 0.064 for the model with the retracted soft body and decreases to 0.053 when extending the soft body. Ordinarily, retracting the soft body into the body chamber would not result in a change in soft body mass, just volume (by compression and the reduction of various void spaces; Table 2). This difference is ignored in the model with the retracted head in order to compare it to the other hydrostatic models herein, all of which have soft bodies that terminate at the aperture.

Ellesmerocerida 3D Hydrostatic Model

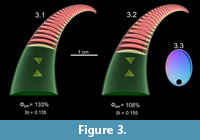Whether the models of the small, rapidly tapering endogastric cyrtocone Plectronoceras (Ellesmerocerida) can be made neutrally buoyant depends upon the body chamber ratio. A possible minimum body chamber ratio (Furnish and Glenister, 1964, p. K146, fig. 81) requires 133% of the available cameral volume to be emptied for a neutrally buoyant condition (Figure 3.1). An additional model (Figure 3.2) is made nearly neutrally buoyant (Φ_gas = 108%) by further shortening the body chamber with the addition of one more camera (body chamber length / total length = 35%). The stability index (S_t) is not of much use during a negatively buoyant condition, but increases as body chamber ratio decreases (0.135, and 0.155 for the corresponding models in Figure 3.1 and 3.2).

Orthocerida 3D Hydrostatic Models

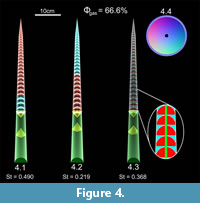A slowly tapering, mesodomic orthocone with a circular whorl section and central siphuncle allows for a neutrally buoyant condition when 66.6% of its available cameral volume is filled with gas and the remaining 33.4% is filled with cameral liquid. The influence of the placement and partitioning of the cameral gas and cameral liquid is explored in Figure 4. The cameral gas (red) in this orthocerid model is placed adapically (Figure 4.1), adorally (Figure 4.2), and as a mixture of 66.6% gas in each camera (Figure 4.3), the sum of which will still equal 66.6% of the total available cameral volume. The adapically placed cameral gas maximizes stability (S_t = 0.490), while adorally placed cameral gas reduces stability to a minimum (S_t = 0.219). Evenly distributing the ratio of gas to liquid in each camera yields a stability index in between these two extremes (S_t = 0.368). Each hydrostatic scenario produces a stable vertical orientation with the aperture inclined downwards.

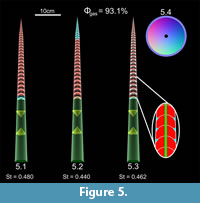Enlarging the body chamber from 33% to 44% of total length (producing a longidome shell) increases the soft body mass by 54 g (Table 2). This change requires a larger volume of the phragmocone to be emptied as compensation, increasing Φ_gas to 93.1% (a 26.5% increase; Figure 5). This modification slightly decreases stability (from 0.490 to 0.480) when the cameral gas is partitioned in the adapical direction, significantly increases stability (from 0.219 to 0.440) when the cameral gas is distributed in the adoral direction, and slightly increases stability (from 0.368 to 0.462) when gas and liquid are partitioned within each camera. The variation in stability is also reduced across the three permutations (Table 2, Figure 5).

Cameral deposits in the orthocerid 3D hydrostatic models were investigated by solving for the appropriate volume during a neutrally buoyant condition with phragmocones completely emptied of cameral liquid (Equation 3). Due to the higher density of cameral deposits relative to cameral liquid, only 13.1% of the total available cameral volumes need to be filled with cameral deposits in order for this model to become neutrally buoyant. 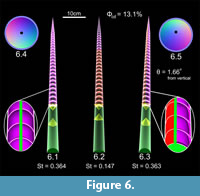Figure 6.1 shows an orthocerid 3D model with evenly placed cameral deposits (purple; 13.1% of each cameral volume) lining the inside of each chamber (simulating episeptal, hyposeptal, and mural cameral deposits). The influence on stability is compared when filling just the apical portion of the shell with the calculated Φ_cd (Figure 6.2) in order for the cameral deposits to act as an ideal counterweight. Figure 6.3 shows an orthocerid 3D model with the same proportion of cameral deposits deposited asymmetrically and weighted in the ventral direction. The siphuncle and septal apices have been displaced in the dorsal direction, which has some subtle difference on the mass distribution as well. This modification causes the shell to rotate so that the aperture is inclined 1.66^o from vertical. In each experiment, the orthocerid 3D models with cameral deposits are stable in a vertical or near vertical syn vivo orientation under static conditions.

Endocerida 3D Hydrostatic Models

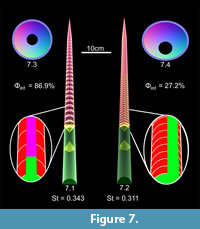The influence of the large, mineralized, siphuncle typical of endocerids on hydrostatic properties was evaluated by modifying the 3D model of the orthocerid to accommodate such a siphuncle (Figure 7.1). The volume of the soft body remained the same, while the shell volume decreased due to the large siphuncular foramina in the septa (Table 2). In order for this model to be neutrally buoyant, 86.9% mineralization of the siphuncle is required. This changes the mass distribution in such a way as to slightly reduce the stability index to 0.343 (that is, by approximately 5.6% of the stability of the orthocerid with symmetrical cameral deposits).

A second 3D hydrostatic model that better represents the overall shell anatomy of an endocerid was constructed by generating a shell with a depressed whorl section (compressed dorso-ventrally) that contains a ventrally displaced siphuncle and closer septal spacing (Figure 7.2). The body chamber ratio to total length (33%) and degree of shell taper remained the same between this model and the orthocerid model. The ventral displacement of the siphuncle does not significantly rotate the model (unlike the orthocerid model in Figure 6.3). The increased mass of the shell due to the closer septal spacing (Table 2) reduces the mineralized proportion of the siphuncle to 27.2%. Both of these modifications change the mass distribution so that the center of gravity is moved adapically, reducing the stability index to 0.311. Aside from these modifications, the endocerid 3D hydrostatic models share stable, vertical syn vivo static orientations with the orthocerid 3D models.

Oncocerida 3D Hydrostatic Models

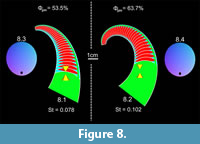
The Oonoceras 3D model with a small body chamber to phragmocone ratio and gentle exogastric curvature requires 53.5% of the phragmocone to be emptied in order to be neutrally buoyant (Figure 8.1). Its stability index is relatively low at 0.078 (Table 2). The larger body chamber to phragmocone ratio in the Euryrizocerina model requires more cameral liquid to be emptied, resulting in a Φ_gas of 63.7% and changing the mass distribution in such a way as to slightly increase the stability index to 0.102 (Figure 8.2; Table 2). The Euryrizocerina 3D model is rotated so that the aperture is tilted further upwards in the dorsal direction than the Oonoceras 3D model (θ = 36.5^o and 26.5^o, respectively).

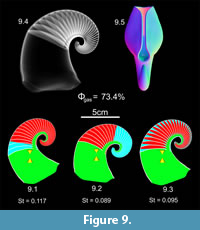Discosorida 3D Hydrostatic Models

The endogastric discosorid 3D model was created with three different shell generation arrays due to its allometric shell taper throughout ontogeny (Table 1). The model of Phragmoceras attains neutral buoyancy when 73.4% of its camerae are emptied of cameral liquid (Figure 9). Syn vivo orientation is heavily dependent upon the distribution of cameral liquid and gas within the phragmocone, while stability is dependent to a lesser extent. Adapically distributed cameral gas rotates the aperture in the ventral direction (Figure 9.1), while adorally distributed cameral gas rotates the aperture in the dorsal direction (Figure 9.2). An even distribution of Φ_gas in of the camerae yields a static orientation in between these two extremes (Figure 9.3). Stability indices follow a similar pattern with little variability, where adapical cameral gas is most stable (St = 0.117), adoral cameral gas is least stable (St = 0.089), and evenly distributed cameral gas and liquid in each camera falls in between (St = 0.095).

DISCUSSION

Hydrostatics of Nautilus pompilius: A Modern Model

Based on observation of living Nautilus, its hydrostatic stability is sufficient to properly orient the living animal, despite the thrust generated during locomotion by expelling water from the mantle cavity through the hyponome. This jet action creates a rocking motion since it slightly displaces the vertical alignment of the centers of buoyancy and gravity, which are then realigned by some restoring moment. Okamoto (1996) computed a stability index for Nautilus pompilius of 0.75, which is much higher than the values of 0.064 and 0.053 calculated here for retracted and extended soft bodies, respectively. This discrepancy is because Okamoto (1996) uses the center of the body chamber as a proxy for the center of gravity. Figure 2.3 and 2.4 show that the center of buoyancy is much lower in the z direction than the center of the phragmocone because the center of buoyancy coincides with the center of volume, which is heavily influenced by the living chamber. The center of gravity is also higher in the z direction than the center of the body chamber. The smaller distance between the true centers of buoyancy and gravity than the centers of the phragmocone and body chamber is responsible for such drastic differences in stability indices between this study and Okamoto (1996). Although the stability indices from these two studies differ, they are both relative and proportionate. The computed stability indices herein can be used to better understand the hydrostatic stability of the other studied morphotypes. Larger stability indices than the Nautilus would have had a greater restoring moment acting to keep the center of gravity vertically aligned under the center of buoyancy.

Comparison of the retracted vs. extended soft bodies in the Nautilus pompilius hydrostatic models provides insight on the influence of terminating the soft body at the aperture for all Paleozoic hydrostatic models investigated here. Since the living Nautilus with an extended soft body displaces more of the medium in which it is submerged, it requires a lower organismal mass to keep it neutrally buoyant (increasing Φ_gas from 74.3% in the retracted soft body model to 83.6% with the soft body extended). For the model with the extended soft body, Φ_gas is similar to the adult range reported in Ward (1979), which was 88% to nearly 100%. An extended soft body also slightly reduces stability (from 0.064 to 0.053) because the center of buoyancy is weighted by the soft body displacing more liquid. This also influences the center of gravity because of a larger contribution to the total mass distribution by the soft body. Since retraction/extension of the soft body changes the relative positions of the centers of buoyancy and gravity, the living animal’s orientation also slightly changes. The Nautilus pompilius hydrostatic model with the extended soft body is rotated in the ventral direction when compared to the retracted soft body model (apertural angle rotated from 64^o retracted to 47^o). All of these modifications are expected to subtly influence the hydrostatic properties of the Paleozoic models of this study due to unknown soft body morphologies.

Hydrostatics of Ellesmerocerida: Constraints on Neutral Buoyancy

The 3D hydrostatic model of the endogastric brevicone, Plectronoceras (Ellesmerocerida), suggests that this genus may have struggled to achieve neutral buoyancy (Westermann, 1998). If the soft body morphology permitted, this genus and similar morphotypes could have had to continuously swim in order to stay in the water column. This restriction is a result of the poor cameral volume capacity due to the shape of the phragmocone (relatively rapid taper and large body relative to cameral volumes; Furnish and Glenister, 1964, Westermann, 1998), which prevents compensation for the sum of the organismal mass by simply emptying cameral liquid (Figure 3; Table 2). The interpretation of a negatively buoyant and neritic mode of life for this morphotype is consistent with the absence or extremely rare occurrence of small breviconic ellesmerocerids in deep, distal marine settings during the Early Ordovician (Kröger et al., 2009). Requiring continuous active locomotion would be exhaustive for these morphotypes to remain above anoxic bottom waters. During the Middle Ordovician, ellesmerocerids in oceanic settings became more common probably as a result of more longiconic and relatively orthoconic forms appearing within this clade (Kröger et al., 2009). However, during the Late Ordovician just before their extinction, the ellesmerocerids were once again confined to neritic settings (Teichert and Moore, 1964; Frey et al., 2004; Kröger et al., 2009). Although the stability index of the ellesmerocerid model is of little interpretive use in a negatively buoyant condition, it could be used in a relative manner to understand how well the shell can remain upright due to an interaction with moving water. The center of buoyancy is still significantly above the center of gravity, which would position the phragmocone to be inclined in a near vertical syn vivo orientation above the soft body. In the case of a completely emptied phragmocone (where the sum of the cameral mass is essentially zero) filling the camerae with liquid would reduce stability by moving the center of gravity closer to the center of buoyancy.

Body chamber length, which is largely unknown for Plectronoceras (Teichert, 1964; Chen and Teichert, 1983), influences the conditions for neutral buoyancy. In order for these models to attain neutral buoyancy, body chamber length has to be reduced to approximately 35% of the total length. However, the additional mass from the unknown soft body extending out of the shell should slightly influence the organismal weight relative to the buoyant force and make neutral buoyancy even more difficult. A conch with minimum estimates of body chamber proportions (40% body chamber length to total length; Figure 3.1) does not have the cameral volume capacity to completely reduce weight. The calculated difference between the mass of the water displaced (producing buoyant force) and the total mass of the organism is only 1.815 g. Hence, while negatively buoyant, the hydrostatic properties of the ellesmerocerid shell would have significantly reduced the effective weight of the organism (Table 2), which may have prevented it from sinking into a very soft substrate. Also, although the soft part morphology of ellesmerocerids is poorly known, relatively robust tentacles and a hyponome could have permitted ellesmerocerids of this general morphotype to function in a similar manner to the extant coleoid Metasepia pfefferi, a small, negatively buoyant cuttlefish with a very limited swimming capacity (Roper and Hochberg, 1988; Reid et al., 2005). Given its very low effective weight, the ellesmerocerid may have been able to briefly rise from the seafloor (maintaining a near vertical orientation) if enough thrust could be produced either by pushing with its tentacles or jetting water through its hyponome. This small upward jump could have been enough to avoid a benthic predator. Since the Plectronoceras models in the current study are approximations based on incompletely known morphologies, additional specimens are required to truly understand the hydrostatics of these morphotypes. Differences in the unknown apex morphology or adoral shell could have altered the conditions for neutral buoyancy by improving cameral volume capacity relative to the organismal mass.

Hydrostatics of Orthocerida: Influence of Body Chamber Length and Cameral Deposits

All orthocerid hydrostatic models (Figure 4, Figure 5, Figure 6) can attain neutral buoyancy with a vertical syn vivo orientation in static conditions. While the distribution of cameral liquid in the phragmocone is explored in many models within the current study, there is no evidence that suggests siphunculate cephalopods had the ability to selectively modify the placement of cameral liquid in their chambers (Ward, 1979). Cameral liquid can only be significantly modified in camerae through which the siphuncle passes, although it does not necessarily have to be directly in contact (coupled) with the cameral liquid to be removed (Jacobs, 1996). Cameral liquid transport depends on the osmotic gradient between the siphuncle and camerae, and therefore cannot be selectively altered within a single camera (aside from siphuncular plugs, changes in removal of cameral liquid throughout ontogeny, and the fact that septal formation must occur in a flooded chamber; Ward, 1979). Therefore, the true distribution of cameral liquid lies between the hydrostatic models simulating adorally placed cameral liquid and an even distribution of Φ_gas in each camera (Figure 4.1 and 4.3).

The hydrostatic experiment of adapically distributed cameral gas in the phragmocone of an orthocerid model was prompted by the experiments by Westermann (1977), who suggested that cameral liquid can be positioned at the apex of an orthocone shell to place the center of gravity at the same location as the center of buoyancy. This scenario depends upon the appropriate volume of cameral liquid for a neutrally buoyant condition (which is also dependent upon the body chamber ratio, and volumes of every object with unique density). Cameral liquid cannot be used as a true counterweight because it is of lower density and volume than the average materials on the adoral side of the center of buoyancy. Westermann (1977, 1998) is correct about the tendency of the center of gravity to move in the adapical direction as the volume of cameral liquid is moved in the same direction. However, care must be taken when assuming that siphunculate, ectocochleate cephalopods were capable of such modifications, and it must be remembered that the total organismal mass must not exceed the mass of the water displaced for neutral buoyancy to persist.

A mesodome body chamber ratio (~33% total length) for the orthocerid models (Figure 4) requires 66.6% of its chambers to be emptied in order to be neutrally buoyant. Increasing the body chamber ratio to 44% total length requires 26.5% more of the cameral volume to be emptied in order to compensate for the mass increase of 54g (Table 2). Body chamber length is well known to be a constraining factor on neutral buoyancy (Trueman, 1941; Westermann, 1977, 1998, 2013; Saunders and Shapiro, 1986; Okamoto, 1996). The hydrostatic experiments shown in Figure 4 and Figure 5 confirm that the mass increase of the larger body chamber is much greater than the reduction of shell mass from fewer septa. However, the common consensus with planispiral ectocochleates is that body chamber length is inversely proportional to stability (Saunders and Shapiro, 1986; Okamoto, 1996; Westermann, 1998). This relationship is not necessarily true for orthoconic shell forms. When the body chamber ratio is increased, stability is very slightly reduced only for the case of adapically distributed cameral gas (Figure 5.1). For the hydrostatic scenarios where cameral gas is distributed adorally (Figure 5.2) or evenly distributed in each camera (Figure 5.3), increasing the body chamber ratio actually increases stability. The center of buoyancy remains constant between all orthocerid models because the external shell does not change shape and maintains a common center of volume. However, the centers of gravity are influenced by the distributions of objects of unique densities, which shift the total mass distribution in the adoral or adapical directions. Increasing the body chamber length from 33% to 44% is allowed by the removal of three septa in the phragmocone, which displaces cameral liquid in such a way that moves the center of gravity in the adapical direction (towards the center of buoyancy), slightly reducing stability. The center of gravity is moved adorally (away from the center of buoyancy) for the hydrostatic scenarios of cameral gas distributed adorally, or evenly amongst all camerae, mostly due to the decreased volume (and therefore mass) of cameral liquid in the phragmocone. Planispiral ectocochleate hydrostatics may function in a similar manner, where stability (and possibly orientation) are extremely dependent upon the distribution of cameral liquid, as well as the influences of each material of unique density on the total mass distribution.

Cameral deposits in orthocerids have been hypothesized to act as “counterweights” to permit a horizontal orientation (Westermann, 1977, 1998). This view assumes that such deposits were accumulated during life and not via diagenetic processes (Mutvei, 2018). Cameral deposits would act as much more efficient counterweights than cameral liquid because they are stationary and of a much higher density (~2.62 g/cm³) than the soft body (1.065 g/cm³). Similar to cameral liquid in the phragmocone, cameral deposits can only occupy a certain percentage of the phragmocone for the cephalopod to remain neutrally buoyant (so that the total organismal mass does not exceed the mass of the water displaced). The orthocerid hydrostatic model with a phragmocone emptied of cameral liquid requires 13.1% of its available cameral volume occupied by cameral deposits to be neutrally buoyant (Figure 6.1). These deposits are evenly distributed within each camera and cover the mural portions of the internal shell and both sides of each septum. The volume of cameral deposits corresponds to the same mass of liquid required for neutral buoyancy. The total mass distribution is altered in such a way as to very slightly reduce stability from the hydrostatic model where cameral gas is evenly distributed in each camera (Figure 4.3). However, when the cameral deposits are distributed solely in the adapical direction (filling the entirety of each camera so that 13.1% of total cameral volume is occupied) stability is significantly reduced to 0.147 (Figure 6.2). Cameral deposits in orthocerids are commonly found to increase in volume relative to each camera approaching the apex (Teichert, 1964b), therefore the actual hydrostatic influence of cameral deposits would lie between the models in Figure 6.1 and 6.2. While cameral deposits distributed in this manner only yield vertical syn vivo static orientations, they are capable of reducing stability depending on their distribution within the phragmocone. This reduction in stability may be necessary in order to deviate from a vertical position by the active use of the hyponome. Lower stability indices would reduce the energy expended by the living animal to modify its orientation.

The proportion of cameral deposits in the orthocerid models (Figure 6) appear to be relatively low compared to other specimens when comparing median sections (Sweet, 1964; Teichert et al., 1964; Seuss et al., 2012; Mutvei, 2018). This difference could be due to the difficulty in separating the pre-mortem deposits (if they existed) with post-mortem deposits (compare Seuss et al., 2012 and Mutvei, 2018). If all of these cameral deposits are indeed pre-mortem, such large volumes could result in negative buoyancy. The models in the current study (Figure 6) suggest negative buoyancy would result when cameral deposits fill more than 13.1% of the phragmocone. If they are in fact post-mortem (diagenetic), orthocerids and similar orthocones would have had the hydrostatic properties of the models without such deposits (Figure 4). In future studies regarding cameral deposits, the relative volume of cameral deposits to the available cameral volume should be considered because they may be constrained by hydrostatics.

The orthocerid model with a dorsally displaced siphuncle and asymmetrical cameral deposits distributed in the ventral direction yields moderate stability and rotates the shell away from vertical by a negligible amount. This angle would increase when the distribution of the cameral deposits is moved adapically, reducing stability in a similar manner to the hydrostatic model of Westermann (1977). Again, there are space limitations within the shell and a fixed volume of deposits to work with to maintain neutral buoyancy. Positioning the center of gravity under the center of buoyancy in the ventral direction, as required for a horizontal syn vivo static orientation, is a difficult balancing act that is hard to achieve due to the decreasing cameral volumes toward the apex. A perfect horizontal orientation is unlikely under static conditions alone and would probably require active locomotion by use of the hyponome.

The geometry of the orthocerid hydrostatic models supports the idea that taxa sharing this morphotype were capable of active and/or passive swimming in a pelagic habitat due to their capacity for neutral buoyancy. This conclusion is supported by the appearance of these morphotypes in distal marine settings around the globe during the Mid-Tremadocian (Kröger et al., 2009) and is instrumental in their paleobiogeographic dispersal around the globe (Westermann, 1998; Kröger and Zhang, 2009; Kröger et al., 2009). Their syn vivo static orientations are very stable in a vertical orientation, except for taxa with cameral deposits that reduce stability or rotate the shell to a sub-vertical orientation. Active locomotion would have been necessary to further deviate from these orientations, which would have required less energy as hydrostatic stability decreased. This inferred variability in orientation is supported by the preservation of color patterns on orthocerid fossils that either surround the entire circumference of the shell (which indicates a vertical orientation), or a pattern that is restricted to the dorsum (i.e., countershading for a near-horizontal orientation) (Packard, 1988; Westermann, 1998; Kröger et al., 2009; Manda and Turek, 2015).

Hydrostatics of Endocerida: Influence of a Large Siphuncle and Endosiphuncular Deposits

In order to compare the change in hydrostatics between the orthocerid 3D models (Figure 4, Figure 5, Figure 6) and the endocerids with a large siphuncle and mineralized endosiphuncular deposits, the orthocerid model was modified to have a large siphuncle similar to that of Endoceras. By holding the septal spacing, body chamber ratio, shell taper, and thicknesses constant, the mass required to keep the model neutrally buoyant (mineralized endosiphon) is distributed in the apical 86.9% of the siphuncle (Figure 7.1). Such a large mineralized percentage of the siphuncle only slightly reduces stability because its mass distribution is still centered relatively close to the body chamber (compare with Figure 6.2). This endocerid model (Figure 7.1) was modified further in order to have characteristics more similar to a true Endoceras (including closer septal spacing, dorso-ventral compression, and a ventrally displaced siphuncle; Figure 7.2). The total mass of the shell increases from the larger number of septa in the phragmocone (Table 2), yielding a smaller percentage of cameral deposits occupying the siphuncle (27.2%). Since these deposits extend from the apical region, their distribution, albeit a lower volume, reduces stability by moving the center of gravity adapically. The ventral displacement of the siphuncle does not significantly rotate the shell (less than one degree tilting of the aperture toward the dorsum), suggesting a likely vertical syn vivo static orientation. The siphuncular characteristics only seem to reduce stability for the more realistic endocerid model (Figure 5.2). The distinctive endocerid siphuncle may be a modification to ease deviation from a vertical static orientation by active locomotion in a similar manner to the adapically distributed cameral deposits of the orthocerid model (Figure 6.2). Because the locomotive ability of these cephalopods is speculative, we do not know how easy it was to deviate from this vertical orientation. If endocerids behaved as suspension feeders (Mironenko, 2018), they would have had to rely on some active locomotion in order to do so in a horizontal manner. If endocerids were not able to overcome their restoring moments, a demersal lifestyle feeding on benthic elements would be more likely (Frey, 1989; Kröger and Zhang, 2009; Mironenko, 2018).

The larger average size of the endocerids (Teichert and Kummel, 1960) makes it difficult to understand their distribution between neritic and pelagic waters. Post mortem drifting is more common in these forms (see interpretations by Kröger et al., 2009; Kröger and Zhang, 2009). Aside from this, most endocerids are interpreted as demersal predators (Flower, 1964; Frey, 1989; Westermann, 1998; Kröger and Zhang, 2009) that largely occupied epeiric seas (Kröger and Zhang, 2009). However, the relative distribution of these taxa shifted from shallow to deep, distal waters from the Middle Ordovician to Late Ordovician, which was contemporaneous with their drop in biodiversity (Kröger et al., 2009) and origination rates (Teichert, 1964b). The hydrostatic experiments of this study only have implications for the more common longi-orthoconic endocerids with endocones, including some Protocameroceratidae and most Endoceratidae. The studied morphotype excludes the families Thylacoceratidae, Manchuroceratidae, Piloceratidae, Chihlioceratidae, and others with generally primitive siphuncular characteristics, and/or brevi-cyrtocones, many of which were extinct by the end of the Early Ordovician. The longi-orthoconic morphotypes investigated in the hydrostatic experiments herein, either in shallow epeiric or deep distal habitats, would have had a vertical static orientation, probably hovering just above the seafloor. Improving their field of view while scanning the seafloor would have to be altered by active locomotion, which may have been eased by stability-reducing counterweights in the form of endosiphuncular deposits. The hydrostatics of endocerids throughout ontogeny were probably not constant. The apical portions of the phragmocone have a much larger endosiphon relative to the juvenile whorl height (a feature that was not modeled in the current study), and therefore these morphotypes were probably negatively buoyant in their very early life stages (Teichert, 1964b; Westermann, 1998; Kröger et al., 2009). This difference between juvenile and adult hydrostatics also partially explains the bimodal distribution of Endocerida between neritic and oceanic zones during the Ordovician.

Hydrostatics of Oncocerida: Investigation of Body Chamber Ratio and Exogastric Shell Curvature

Oncocerida is an incredibly diverse group with strongly curved brevicones, some longicones, few torticones, and relatively common apertural modifications (including elaborate constrictions and bottle-necked mature apertures; Sweet, 1964; Westermann, 1998). This taxon was most common and diverse within low latitude, shallow water and reef paleoenvironments (Westermann, 1998; Kröger and Zhang, 2009; Kröger, 2013). Only the hydrostatics of exogastric cyrtocones are investigated in this study, which are modeled after two genera, Oonoceras and Euryrizocerina (Figure 8). The former genus has a shorter body chamber ratio, lower degree of exogastric curvature, and a more rapid degree of taper when compared to the latter genus. The hydrostatic 3D models of both genera are capable of attaining neutral buoyancy, which is in contrast to the observations of several authors who suggest that the typical brevi-cyrtocone morphology could not reduce enough weight to equal the buoyant force of the organism (Flower, 1957; Yochelson et al., 1973; Blind, 1987; Frey, 1989). The Oonoceras hydrostatic model requires less of its phragmocone to be emptied (Φ_gas = 53.5%) when compared to the Euryrizocerina model (Φ_gas = 63.7%) due to its shorter body chamber to phragmocone ratio (Table 2).

The Oonoceras had a gentler shell curvature than Euryrizocerina, which is very influential on the total mass distribution, yielding different apertural orientations (26.5^o and 36.5^o rotation of the apertures toward the dorsum, respectively). As exogastric coiling becomes more extreme, the relative positions of the centers of buoyancy and gravity are arranged so that the aperture is further rotated in the dorsal direction. The involute shell of Nautilus pompilius (Figure 2) serves as an end member of this behavior within this study, dorsally rotating the aperture to 64^o. The dorsal rotation of the aperture with increasing coiling would position the soft body to sense and interact with more of the water column, which may have been an important selective factor in the evolution of more and more strongly coiled cephalopods adapted for life away from the seafloor. The studied oncocerids have similar hydrostatic stability values to the Nautilus pompilius model, suggesting a similar hydrodynamic restoration (rocking) would have taken place when displaced from the equilibrium condition.

The syn vivo static orientations and low stability indices (Figure 8; Table 2) support the interpretation of these oncocerid morphotypes operating as demersal, poor swimmers that were sluggish in both the vertical and horizontal directions (Westermann, 1998). A diagonally oriented aperture would make swimming within the horizontal plane difficult without substantial rocking. A rocking motion during movement would also be exacerbated by the low hydrostatic stability computed for these morphotypes. A slow, saltating habit is likely to have taken place within neritic waters, as supported by their distribution in shallow-water facies and their hydrostatic properties (Westermann, 1998; Kröger and Zhang, 2009; Kröger et al., 2009; Manda and Turek, 2009; Kröger, 2013). This interpretation is also reinforced by the preservation of color patterns within Euryrizocerina, which consist of irregular transverse bands that cover the dorsum and venter (Manda and Turek, 2009). Patterns with a similar circumferential distribution are common for the brevi/cyrtoconic morphotypes (Sweet, 1964). Perhaps cyrtocones with improved look directions (that is, larger field of view) like Euryrizocerina could have operated in a more nekto-benthic fashion than straighter breviconic oncocerids that were restricted to facing downwards (Manda and Turek, 2009). The hydrostatic properties of the Oncocerida may be involved in their role as the ecological successors of the ellesmerocerids (along with the Discosorida) during the Middle to Late Ordovician (Kröger and Zhang, 2009; Kröger, 2013).

Hydrostatics of Discosorida: Cameral Liquid Distribution and Adult Apertural Modification within the Genus Phragmoceras

The endogastric cyrtoconic shell of the discosorid Phragmoceras underwent a unique apertural constriction during its adulthood (Teichert, 1964c; Westermann, 1998). This structure consists of a small dorsal opening and a ventral hyponomic sinus connected by a very constricted section of the aperture (Figure 9.4-9.5). Unlike the endogastric ellesmerocerid hydrostatic model, with a relatively small phragmocone, the Phragmoceras has living chamber to phragmocone ratio sufficient for neutral buoyancy (requiring 73.4% of its camerae to be emptied; Figure 9.1-9.3). The values of hydrostatic stability are of similar magnitude to the Nautilus pompilius model. The orientation of this model is heavily dependent upon the distribution of cameral liquid within the phragmocone, unlike the results of the orthocerid experiments (Figure 4-Figure 5), where only stability is influenced by cameral liquid distribution. Now that shell curvature is involved, the distribution of cameral liquids can actually act as a counterweight to modify orientation. An adapically emptied phragmocone with the cameral liquid distributed in the adoral direction yields an orientation where the aperture is rotated toward the venter, while the opposite is true for an adorally emptied phragmocone. As mentioned above, siphunculate cephalopods could not selectively change the distribution of cameral liquid in the phragmocone, so an orientation between the adapically emptied model (Figure 9.1) and the model with evenly emptied camerae (Figure 9.3) is most likely. This orientation is intriguing because the dorsal opening of the aperture would have allowed the soft body and arms to be directed downward towards the substrate (as suggested by Westermann, 1998). The hyponomic sinus would have also been elevated in the ventral direction, so that forward locomotion would have been more efficient; that is, the thrust generated from the hyponome would be transmitted into more translational movement than rotational movement. The ideal orientation for perfect translational movement would occur when the center of the hyponome was horizontally aligned with the static pivot point of the living organism (directly between the centers of buoyancy and gravity). The hydrostatic orientation and ventrally tilted hyponomic sinus of Phragmoceras allow the adapically emptied model (Figure 9.1) to be tilted 22^o below this ideal orientation, while the model with evenly emptied camerae (Figure 9.3) is tilted 33^o from the ideal orientation. This is a significant improvement from the other hydrostatic models of this study, which have their hyponomes orientated close to 90^o from the ideal direction for horizontal (lateral) translation. This orientation is also beneficial given the relatively low hydrostatic stability of this morphotype. The downward direction of the dorsal opening and inclined position of the hyponomic sinus imply that this morphotype was well-adapted to bottom-feeding and forward horizontal movement (as suggested by Westermann, 1998). This function and life habit would perform well in neritic waters, which also agrees with the fossil distribution of the endogastric Discosorida (Westermann, 1998; Manda, 2008; Kröger et al., 2009; Kröger and Zhang, 2009).

CONCLUSIONS

During the Early and Middle Ordovician, ectocochleate cephalopods rapidly diversified and began to shift their distributions from shallow, neritic habitats to nearly every marine paleoenvironment around the globe, including deep/distal settings (Frey et al., 2004; Kröger et al., 2009; Kröger and Zhang, 2009). To better understand how evolutionary changes in shell morphology contributed to this diversification and dispersal into the water column, complex 3D digital models were constructed for six common Early and Middle Ordovician cephalopod morphotypes from several higher taxa of Nautiloidea and Endoceratoidea. These models were used to compute the conditions necessary to achieve neutral buoyancy as well as to characterize the static orientation and hydrostatic stability of these ectocochleate cephalopods during life.

The Plectronoceras model with an endogastric cyrtocone typical of the oldest nautiloid group, Ellesmerocerida, was not capable of neutral buoyancy with the estimated proportions. However, the phragmocone would have significantly reduced the effective weight of the animal, allowing it to sit on a soft substrate without sinking, and briefly push up off the seafloor with minimal effort. With reduction of body chamber length (below approximately 35% of total length in the studied model), such shells can improve their cameral volume capacity so that a neutrally buoyant condition is achieved. In contrast, the endogastric cyrtocone of the discosorid, Phragmoceras, was capable of neutral buoyancy, and its syn vivo orientation and adult modifications of the aperture suggest that it was well adapted to forward swimming (albeit sluggishly) as a bottom feeder. The exogastric cyrtocones of the oncocerids would also have been capable of neutral buoyancy and slow horizontal swimming, however their aperture would be more dorsally rotated, suggesting greater interaction with items in the water column as opposed to the ancestral bottom-facing orientation. The hydrostatic attributes of the discosorid and oncocerid morphotypes, especially their ability to attain neutral buoyancy, may have played an important role in their ecological takeover of shallow neritic water from the ellesmerocerids during the Middle to Late Ordovician (Kröger and Zhang, 2009; Kröger, 2013). The stability indices of these neutrally buoyant cyrtocones are also similar to the fully coiled Nautilus pompilius, suggesting similar hydrodynamic capabilities (specifically in terms of restoration to equilibrium conditions) despite differing syn vivo orientations, shell morphologies, and fossil distributions.

All straight orthocone models, representing forms common in orthocerids and endocerids, have a stable vertical orientation. While cameral liquid distribution would influence stability, only cameral or endosiphuncular deposits would act as a true counterweight. However, it is unlikely such deposits would be sufficient to rotate the shell to a horizontal life orientation, implying that orthoconic cephalopods would need to employ active locomotion to achieve such a position in the water column. The hydrostatics of these morphotypes reinforce fossil occurrences of these orthoconic taxa in the Early and Middle Ordovician in distal marine settings around the globe (Kröger et al., 2009). Whether occupying a pelagic, deep, distal habitat (as suggested for many orthocerids and some endocerids; Westermann, 1998; Kröger et al., 2009), or demersal habitats in shallow, epeiric seas (many endocerids and some orthocerids; Westermann, 1998; Kröger et al., 2009), these morphotypes had the capacity to act as neutrally buoyant vertical migrants and potentially active swimmers, which may have been key to their extensive paleobiogeographic dispersal.

ACKNOWLEDGMENTS

We thank P. Minister for supplying the Nautilus pompilius soft body 3D model used in hydrostatic simulations. We also thank the editor and reviewers for their time and comments that significantly improved the manuscript.

REFERENCES

Autodesk Inc. 2017a. Meshmixer 3.3. Autodesk Inc., San Rafael, California.

Autodesk Inc. 2017b. Netfabb 2017.3. Autodesk Inc., San Rafael, California.

Blender Online Community. 2017. Blender, a 3D Modelling and Rendering Package. Blender Institute, Amsterdam. http://www.blender.org

Blind, W. 1987. Comparative investigations on the morphology and structure of Nautilus pompilius, Orthoceras sp., Pseudorthoceras sp., and Kionoceras sp. Palaeontographica A, 198:101-128.

Chen, J. and Teichert, C. 1983. Cambrian Cephalopoda of China. Palaeontolographica, 181:1-102.

Cignoni, P. and Ranzuglia, G. 2014. MeshLab (Version 1.3.3) [Computer graphics software]. Visual Computing Lab - ISTI - CNR Pisa, Italy. Available from http://meshlab.sourceforge.net

Cowen, R., Gertmann, R., and Wiggett, G. 1973. Camouflage patters in Nautilus, and their implications for cephalopod paleobiology. Lethaia, 6:201-214. https://doi.org/10.1111/j.1502-3931.1973.tb01193.x

Denton, E. and Gilpin-Brown, J. 1966. On the buoyancy of the pearly Nautilus. Journal of the Marine Biological Association of the United Kingdom, 51:723-759.

Ebel, K. 1983. Berechnungen zur Schwebfähigkeit von Ammoniten. Neues Jahrbuch für Geologie und Paläontologie, Monatshefte, 1983:614-640.

Flower, R.H. 1957. Nautiloids of the Paleozoic. Geological Society of America Memoir, 67(2):829-852.

Flower, R.H. 1964. Nautiloid shell morphology. Memoir - New Mexico Institute of Mining and Technology, State Bureau of Mines and Mineral Resources, 13:1-77.

Frey, R.C. 1988. Paleoecology of Treptoceras duseri (Michelinoceratida, Proteoceratidae) from Late Ordovician of southwestern Ohio. New Mexico Bureau of Mines and Mineral Resources Memoir, 44:79-101.

Frey, R.C. 1989. Paleoecology of a well-preserved nautiloid assemblage from a Late Ordovician shale unit, southwestern Ohio. Journal of Paleontology, 63:604-620. https://doi.org/10.1017/S0022336000041238

Frey, R.C., Beresi, M.S., Evans, D.H., King, A.H., and Percival, I.G. 2004. Nautiloid cephalopods, p. 209-213. In Webby, B., Paris, F., Droser, M., and Percival, I. (eds.), The Great Ordovician Biodiversification Event. Columbia University Press, New York. https://doi.org/10.7312/webb12678-022

Furnish, W.M. and Glenister, B.F. 1964. Nautiloidea - Ellesmerocerida, p. K129-K159. In Moore, R.C. (ed.), Treatise on Invertebrate Paleontology, Vol. K, Mollusca, Part 3. Geological Society of America and University of Kansas Press, Boulder, Colorado and Lawrence, Kansas.

Greenwald, L. and Ward, P.D. 1987. Buoyancy in Nautilus, p. 547-560. In Saunders, B.W. and Landman, N.H. (eds.), Nautilus—The Biology and Paleobiology of a Living Fossil. Springer, Dordrecht. https://doi.org/10.1007/978-90-481-3299-7_34

Hewitt, R.A. and Watkins, R. 1980. Cephalopod ecology across a Late Silurian shelf tract. Neues Jahrbuch für Geologie und Paläontologie, Abhandlungen, 160:96-117.

Hoffmann, R., Schultz, J.A., Schellhorn, R., Rybacki, E., Keupp, H., Gerden, S.R., Lemanis, R., and Zachow, S. 2014. Non-invasive imaging methods applied to neo- and paleo-ontological cephalopod research. Biogeosciences, 11:2721-2739. https://doi.org/10.5194/bg-11-2721-2014

Hoffmann, R., Lemanis, R., Naglik, C., and Klug, C. 2015. Ammonoid buoyancy, p. 613-648. In Klug, C., Korn, D., De Baets, K., Kruta, I., and Mapes, R. (eds.), Ammonoid Paleobiology: From Anatomy to Ecology, Topics in Geobiology, vol. 43. Springer, Dordrecht. https://doi.org/10.1007/978-94-017-9630-9_16

Hoffmann, R., Lemanis, R., Falkenberg, J., Schneider, S., Wesendonk, H., and Zachow, S. 2018. Integrating 2D and 3D shell morphology to disentangle the paleobiology of ammonoids: a virtual approach. Palaeontology. 61:89-104. https://doi.org/10.1111/pala.12328

Inoue, S. and Kondo, S. 2016. Suture pattern formation in ammonites and the unknown rear mantle structure. Scientific Reports, 6:33689. https://doi.org/10.1038/srep33689

Jacobs, D.K. 1996. Chambered cephalopod shells, buoyancy, structure and decoupling: History and red herrings. Palaios, 11:610-614. https://doi.org/10.2307/3515195

Klinger, H.C. 1980. Speculations on buoyancy control and ecology in some heteromorph ammonites, p. 337-355. In House, M.R. and Senior, J.R. (eds.), The Ammonoidea, Systematics Association Special Volume 18. Academic Press, London.

Klug, C. and Hoffmann, R. 2015. Ammonoid septa and sutures, p. 45-90. In Klug, C., Korn, D., De Baets, K., Kruta, I., and Mapes, R.H. (eds.), Ammonoid Paleobiology: From Anatomy to Ecology, Topics in Geobiology, vol. 43. Springer, Dordrecht. https://doi.org/10.1007/978-94-017-9630-9_3

Kröger, B. 2007. Concentrations of juvenile and small adult cephalopods in the Hirnantian cherts (Late Ordovician) of Porkuni, Estonia. Acta Palaeontologica Polonica, 52:591-608.

Kröger, B. 2013. The cephalopods of the Boda Limestone, Late Ordovician, of Dalarna, Sweden. European Journal of Taxonomy, 41:1-110. https://doi.org/10.5852/ejt.2013.41

Kröger, B. and Zhang, Y. 2009. Pulsed cephalopod diversification during the Ordovician. Palaeogeography, Palaeoclimatology, Palaeoecology, 273:174-183. https://doi.org/10.1016/j.palaeo.2008.12.015

Kröger, B., Servais, T., and Zhang, Y. 2009. The origin and initial rise of pelagic cephalopods in the Ordovician. PLoS ONE, 4(9):e7262. https://doi.org/10.1371/journal.pone.0007262

Kröger, B., Vinther, J., and Fuchs, D. 2011. Cephalopod origin and evolution: A congruent picture emerging from fossils, development and molecules. Bioessays, 33:602-613. https://doi.org/10.1002/bies.201100001

Lemanis, R., Korn, D., Zachow, S., Rybacki, E., Hoffmann, R. 2016. The evolution and development of cephalopod chambers and their shape. PlosOne, 11:1-21. https://doi.org/10.1371/journal.pone.0151404

Lemanis, R., Zachow, S., Fusseis, F., and Hoffmann, R. 2015. A new approach using high-resolution computed tomography to test the buoyant properties of chambered cephalopod shells. Paleobiology, 41:313-329. https://doi.org/10.1017/pab.2014.17

Manda, S. 2008. Palaeoecology and palaeogeographic relations of the Silurian phragmoceratids (Nautiloidea, Cephalopoda) of the Prague Basin (Bohemia). Bulletin of Geosciences, 83:39-62. https://doi.org/10.3140/bull.geosci.2008.01.039

Manda, S. and Turek, V. 2009. A Silurian oncocerid with preserved colour pattern and muscle scars (Nautiloidea). Bulletin of Geosciences, 84:755-766. https://doi.org/10.3140/bull.geosci.1168

Manda, S. and Turek, V. 2015. Colour patterns on Silurian orthocerid and pseudorthocerid conchs from Gotland - palaeoecological implications. Estonian Journal of Earth Sciences, 64:74-79. https://doi.org/10.3176/earth.2015.13

Mapes, R.H. and Hoare, R.D. 1987. Annotated bibliography for preservation of colour patterns on invertebrate fossils. The Compass, 65:12-17.

Mironenko, A. 2018. Endocerids: suspension feeding nautiloids? Historical Biology. https://doi.org/10.1080/08912963.2018.1491565

Mutvei, H., Zhang, Y., and Dunca, E. 2007. Late Cambrian plectronocerid nautiloids and their role in cephalopod evolution. Palaeontology, 50(6):1327-1333. https://doi.org/10.1111/j.1475-4983.2007.00708.x

Mutvei, H. 2018. Cameral deposits in Paleozoic cephalopods. GFF, 140:254-263. https://doi.org/10.1080/11035897.2018.1483966

Naglik, C., Monnet, C., Goetz, S., Kolb, C., De Baets, K., Tajika, A., and Klug, C. 2015b. Growth trajectories of some major ammonoid sub-clades revealed by serial grinding tomography data. Lethaia, 48:29-46. https://doi.org/10.1111/let.12085

Naglik, C., Rikhtegar, F., and Klug, C. 2016. Buoyancy of some Palaeozoic ammonoids and their hydrostatic properties based on empirical 3D-models. Lethaia, 49:3-12. https://doi.org/10.1111/let.12125

Naglik, C., Tajika, A., Chamberlain, J., and Klug, C. 2015a. Chapter 17 - Ammonoid locomotion. p. 649-688. In Klug, C., Korn, D., De Baets, K., Kruta, I., and Mapes, R. (eds.), Ammonoid Paleobiology. From Anatomy to Ecology, Topics in Geobiology, vol. 43. Springer, Dordrecht. https://doi.org/10.1007/978-94-017-9630-9_17

Okamoto, T. 1996. Theoretical modeling of ammonoid morphology, p. 225-251. In Landman, N.H., Tanabe, K., and Davis, R.A. (eds.), Ammonoid Paleobiology, Topics in Geobiology, vol. 13. Plenum Press, New York. https://doi.org/10.1007/978-1-4757-9153-2_8

Packard, A. 1988. Visual tactics and evolutionary strategies, p. 89-103. In Wiedmann, J. and Kullmann, J. (eds.), Cephalopods - Present and Past. Schweizerbart’sche, Stuttgart.

Raup, D.M. 1966. Geometric analysis of shell coiling: general problems. Journal of Paleontology, 40:1178-1190.

Raup, D.M. 1967. Geometric analysis of shell coiling: coiling in ammonoids. Journal of Paleontology, 41:43-65.

Raup, D.M. and Chamberlain, J.A. 1967. Equations for volume and centre of gravity in ammonoid shells. Journal of Paleontology, 41:566-574.

Reid, A., Jereb, P. and Roper, C.F.E. 2005. Family Sepiidae, p. 57-152. In Jereb, P. and Roper, C.F.E. (eds.), Cephalopods of the World: An Annotated and Illustrated Catalogue of Cephalopod Species Known to Date, Volume 1. Chambered Nautiluses and Sepioids (Nautilidae, Sepiidae, Sepiolidae, Sepiadariidae, Idiosepiidae and Spirulidae), FAO Species Catalogue for Fishery Purposes, No. 4, Vol. 1. Food and Agriculture Organization of the United Nations (FAO), Rome.

Reyment, R.A. 1958. Some factors in the distribution of fossil cephalopods. Stockholm Contributions to Geology, 1:97-184.

Reyment, R.A. 1974. Factors in the distribution of fossil cephalopods; Part 3, Experiments with exact models of certain shell types. Bulletin of the Geological Institutions of the University of Uppsala, New Series 4, 2:7-41.

Roper, C. and Hochberg, F. 1988. Behavior and systematics of cephalopods from Lizard Island, Australia, based on color and body patterns. Malacologia, 29:153-193.

Saunders, W.B. and Shapiro, E.A. 1986. Calculation and simulation of ammonoid hydrostatics. Paleobiology, 12:64-79. https://doi.org/10.1017/s0094837300002980

Seuss, B., Nützel, A., Mapes, R.H., and Yancey, T.E. 2009. Facies and fauna of the Pennsylvanian Buckhorn Asphalt Quarry deposit: a review and new data on an important Paleozoic fossil Lagerstätte with aragonite preservation. Facies, 55:609-645. https://doi.org/10.1007/s10347-009-0181-9

Seuss, B., Mapes, R.H., Klug, C., and Nützel, A. 2012. Exceptional cameral deposits in a sublethally injured Carboniferous orthoconic nautiloid from the Buckhorn Asphalt Lagerstätte in Oklahoma, USA. Acta Palaeontologica Polonica, 57:375-390. https://doi.org/10.4202/app.2011.0008

Stridsberg, S. 1985. Silurian oncocerid cephalopods from Gotland. Fossils and Strata, 18:1-65.

Swan, R.H. and Saunders, W.B. 1987. Function and shape in Late Paleozoic (Mid-Carboniferous) ammonoids. Paleobiology, 13:297-311. https://doi.org/10.1017/s0094837300008885

Sweet, W.C. 1964. Nautiloidea - Orthocerida, p. K216-K261. In Moore, R.C. (ed.), Treatise on Invertebrate Paleontology, Vol. K, Mollusca, Part 3. Geological Society of America and University of Kansas Press, Boulder, Colorado and Lawrence, Kansas.

Tajika, A., Naglik, C., Morimoto, N., Pascual-Cebrian, E., Hennhofer, D., and Klug, C. 2015. Empirical 3D model of the conch of the Middle Jurassic ammonite microconch Normannites : its buoyancy, the physical effects of its mature modifications and speculations on their function. Historical Biology, 27:181-191. https://doi.org/10.1080/08912963.2013.872097

Teichert C. 1964a. Endoceratoidea, p. K160-K184. In Moore, R.C. (ed.), Treatise on Invertebrate Paleontology, Vol. K, Mollusca, Part 3. Geological Society of America and University of Kansas Press, Boulder, Colorado and Lawrence, Kansas.

Teichert, C. 1964b. Morphology of hard parts, p. K13-K53. In Moore, R.C. (ed.), Treatise on Invertebrate Paleontology, Vol. K, Mollusca, Part 3. Geological Society of America and University of Kansas Press, Boulder, Colorado and Lawrence, Kansas.

Teichert, C. 1964c. Nautiloidea-Discosorida, p. K320-K342. In Moore, R.C. (ed.), Treatise on Invertebrate Paleontology, Vol. K, Mollusca, Part 3. Geological Society of America and University of Kansas Press, Boulder, Colorado and Lawrence, Kansas.

Teichert, C. and Kummel, B. 1960. Size of endoceroid cephalopods. Breviora of the Museum of Comparative Zoology, 123:1-7.

Teichert, C., Kummel, B., Sweet, W., Stenzel, H., Furnish, W., Glenister, B., Erben H., Moore, R., and Zeller, N. 1964. Treatise on Invertebrate Paleontology; Part K, Mollusca 3, Cephalopoda general features, Endoceratoidea, Actinoceratoidea, Nautiloidea, Bactritoidea. Geological Society of America and University of Kansas Press, Boulder, Colorado and Lawrence, Kansas.

Teichert, C. and Moore, R.C. 1964. Classification and stratigraphic distribution, p. K94-K114. In Moore, R.C. (ed.), Treatise on Invertebrate Paleontology, Vol. K, Mollusca, Part 3. Geological Society of America and University of Kansas Press, Boulder, Colorado and Lawrence, Kansas.

Trueman, A.E. 1941. The ammonite body-chamber, with special reference to the buoyancy and mode of life of the living ammonite. Quarterly Journal of the Geological Society, 384:339-383. https://doi.org/10.1144/gsl.jgs.1940.096.01-04.14

Ward, P.D. 1976. Stratigraphy, Paleoecology and Functional Morphology of Heteromorph Ammonites of the Upper Cretaceous Nanaimo Group, British Columbia and Washington. Unpublished PhD dissertation, McMaster University, Department of Geology, Hamilton, Ontario.

Ward, P.D. 1979. Cameral liquid in Nautilus and ammonites. Paleobiology, 5:40-49. https://doi.org/10.1017/s009483730000628x

Westermann, G.E.G. 1977. Form and function of orthoconic cephalopod shells with concave septa. Paleobiology, 3:300-321. https://doi.org/10.1017/s009483730000539x

Westermann, G.E.G. 1996. Ammonoid life and habitat, p. 607-707. In Landman, N.H., Tanabe, K, and Davis, R.A. (eds.), Ammonoid Paleobiology, Topics in Geobiology, vol. 13. Plenum Press, New York. https://doi.org/10.1007/978-1-4757-9153-2_16

Westermann, G.E.G. 1998. Life habits of nautiloids, p. 263-298. In Savazzi, E. (ed.), Functional Morphology of the Invertebrate Skeleton. John Wiley & Sons, Chichester, New York.

Westermann, G.E.G. 2013. Hydrostatics, propulsion and life-habits of the Cretaceous ammonoid Baculites. Revue de Paléobiologie, 32:249-265.

Yacobucci, M.M. and Manship, L.L. 2012. Ammonoid septal formation and suture asymmetry explored with a geographic information systems approach. Palaeontologia Electronica, 14:1-17. 
https://palaeo-electronica.org/2011_1/136/index.html

Yochelson, E., Flower, R.H., and Webers, G.F. 1973. The bearing of the Late Cambrian monoplacophoran genus Knightoconus upon the origin of the cephalopods. Lethaia, 6:273-310. https://doi.org/10.1111/j.1502-3931.1973.tb01199.x